Python使用割圆法求π值-编程知识

Python使用割圆法求π值

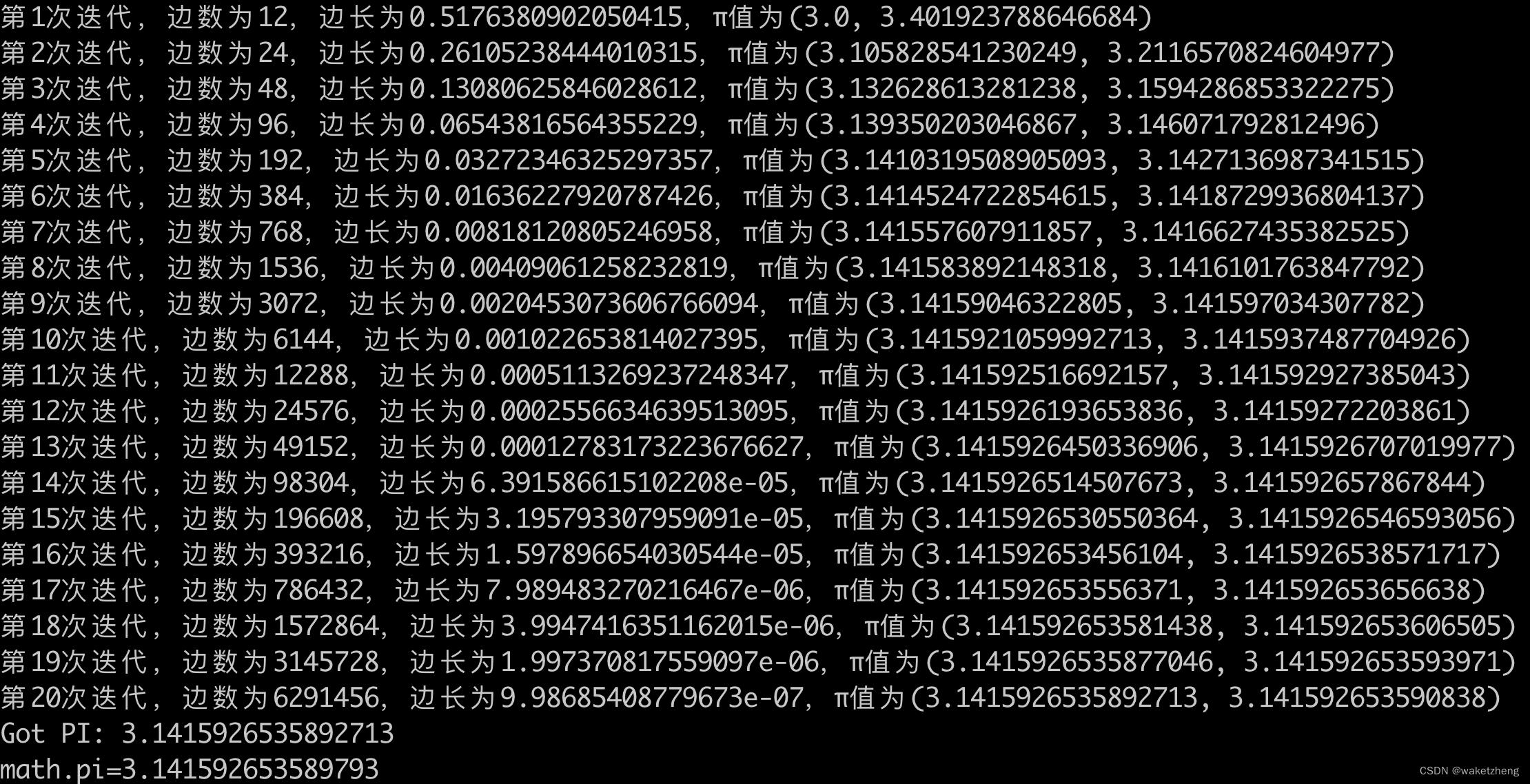
三国时期刘徽提出的割圆法有多牛掰，看这个：刘徽割圆术到底做了什么？ - 知乎

用Python实现的该算法代码如下：

#!/usr/bin/env python
"""使用割圆法计算π值Usage::$ python calc_circle_pi.py 20  # 参数20是迭代次数割圆法的几何描述可参考如下链接：
https://zhuanlan.zhihu.com/p/553830157
https://zhuanlan.zhihu.com/p/340959552
"""import math
import sysdef calc_pi(times: int, *, verbose=False) -> float:"""割圆法求π值:param times: 迭代次数(>=1):param verbose: 是否打印每次迭代的信息"""lines = 6  # 初始边数为6r = length = 1.0  # 边长为1area = (1 * math.sqrt(1**2 - 0.5**2) / 2) * 6  # 面积for i in range(times):lines *= 2  # 边数增加一倍ap = length / 2  # 直角边AP的长度op = math.sqrt(r**2 - ap**2)  # 另一直角边OP的长度pc = r - op  # 新增三角形的短直角边PC的长度length = math.sqrt(ap**2 + pc**2)  # 新多边形的边长ACincr_area = pc * ap / 2  # 新增三角形的面积delta = incr_area * linesarea += deltalow, high = area, area + deltaif verbose:print(f"第{i+1}次迭代，边数为{lines}，边长为{length}，π值为({low}, {high})")if low == high:if verbose:print("已到精度极限，终止迭代。")breakreturn areadef main() -> None:times = 10if sys.argv[1:]:if (a1 := sys.argv[1]) == "-i":times = int(input("请输入迭代次数："))elif a1.isdigit():times = int(a1)print(f"{times = }")pi = calc_pi(times, verbose=True)print(f"Got PI: {pi}\n{math.pi=}")if __name__ == "__main__":main()

结果如下：