1 局限性分析
印度人Torque Minimum 复现
上一篇文章分析了印度人那篇Torque Minimum文章的方法,他的方法存在一些局限性;
1:第一个就是6次转矩脉动的抑制,导致了较大的电流谐波畸变率;
2:第二个就是6次转矩脉动虽然被抑制了,但是相对于其他开关角总的转矩脉动却增大的了。
3:该方法只能针对调制的某一个范围,高于这个调制度就无法实现该功能;
他的优化原则是这样的;
该方法的整体思如下所示:
(1)最小化 Un ;
(2)满足下面三个约束条件;
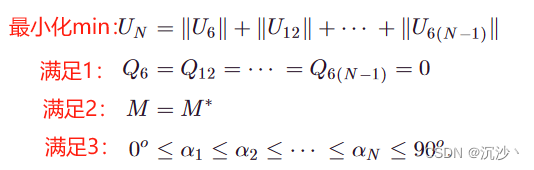
2 改进的分析与探索
2.1 改进策略的分析
我想改进的思路可以被分为几种:
1、可直接达到理想效果的目标,不存在逼近过程,改进思路是使用更好的方法;比如利用优化调制消除6次谐波的方法,该方法达到的目标就是6次谐波的完全消除。改进的出路就在于更快捷的计算速度、更简单的分析方法、离线计算改为在线实现等等;
2、不可达到理想效果的目标,理想效果无法直接达到,改进思路是使用更好的方法逼近目标;比如观测电机角度,不可能完全的跟踪,就需要新的方法去更快速、更接近的观测电机角度;比如基于控制的转矩脉动抑制,有用谐波电流控制器的、有用前馈的、有用学习+前馈的。这些都是应用更加优秀的方法逼近目标。
3、拓展特性,包括 抗参数扰动、鲁棒性、准确性等;
一个文章的贡献一定是针对已有方法所存在的局限性进行一定程度的改善的。
在电控领域离不开稳、准、快三个方面。稳可拓展为稳定性、参数鲁棒性、抗干扰性能;准一般都被定义为准确性,包括指令跟随的准确性、观测结果与真实结果之间的准确性,体现的一个就是误差小,误差越小方法越优秀;快一般可被拓展为响应速度、收敛速度、跟随速度、恢复速度,这些速率上的提升都能被定义为贡献;
在调制领域则多出来一个非控制指标的优化,例如电流THD、转矩THD、系统效率、热损耗等等;这些指标的优化得越低这个方法就越好。或者达到相同的指标,方法更简单,方法执行速度更快,方法兼容性更强等等,它同样存在准确性、快速性、稳定性等指标的衡量,但是更为注重指标本身的优化。
如何将这些改进的思路应用到这篇文章呢?
局限性一定是最为关键的突破点,
优点:实现了6次转矩脉动的完全消除;
局限性1:6次转矩脉动的抑制,导致了较大的电流谐波畸变率;
局限性2:6次转矩脉动虽然被抑制了,但是相对于其他开关角总的转矩脉动却增大的了。
2.2 方法的优化
针对局限性1:怎么在优化转矩基础上,再优化电流THD?
首先是不可否认的是他存在的优越性,就是他将6次转矩脉动谐波完全的抑制为0了。这是其他方法完全无法比较的点。在这个基础上再去进行优化,寻找这个空间。
如下图所示,红色为不同调制度开关角的解集,紫色为六次转矩谐波为0的解集。每个红线与紫线的交集只有2-3个交点,这个解是非常的有限的。换句话说,要想实现6次转矩谐波为0,能够做的选择就只能在这2-3个交点中间去选择,这两三个点非常好对比谁的电流THD更小,选择一个就行了。针对固定的2-3点的改进是非常难以进行的。
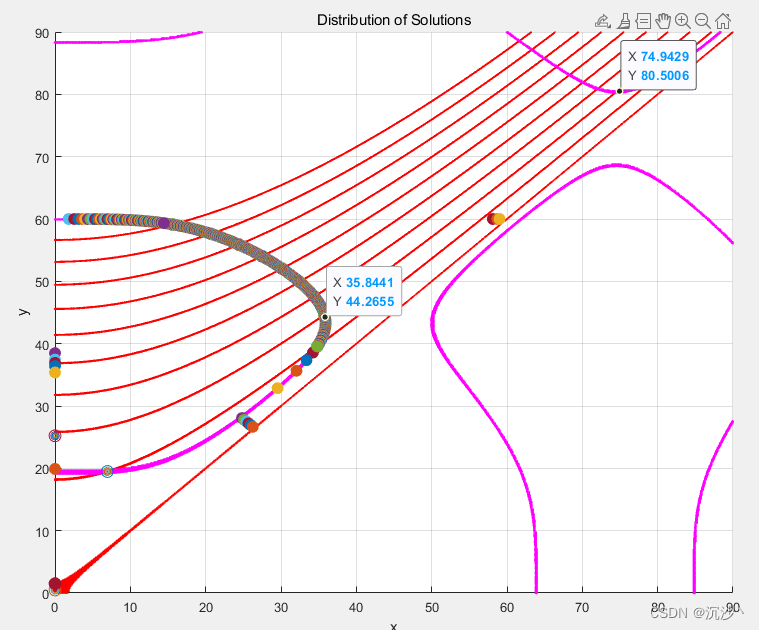
由于满足六次转矩谐波为0这个目标所存在的解集空间非常有限,只有2-3个,在这个基础上再去优化电流THD实际上非常困难。甚至可以翻译过来,在解集只有2-3个的情况下,电流THD是无法被优化的;
针对局限性2:针对六次转矩谐波为0这个目标,在解集只有2-3个的情况下,整体输出转矩脉动大小是无法被进一步压缩的。
所以结论是,针对六次转矩谐波为0这个目标,印度人这篇论文已经是最优的方法了,没有更优秀的方法。目标已定,方法最优,没有任何优化空间。
既然方法无法更改,就寻找一个更为合理的目标。
2.3 目标的优化
既然无法完成方法上的优化,就要针对目标设定上进行改进,也就是目标的优化;
针对局限性1:6次转矩脉动的抑制,导致了较大的电流谐波畸变率;
此时的目标是6次转矩脉动为0,那要是不是0,而是一个范围,这个可能性是不是就大了更多了,是不是就可以寻找电流谐波畸变率更小的点了?
针对局限性2:6次转矩脉动虽然被抑制了,但是相对于其他开关角总的转矩脉动却增大的了。
此时的目标是6次转矩为0,也就是特定转矩谐波消除,却导致了整体转矩波动幅值的增大;那我能不能把目标更改为总体转矩振荡的幅值呢?
上述这两种针对局限性的优化都是可以进行尝试的。
3 优化的探索
3.1 针对局限性1:(6次转矩脉动的抑制,导致了较大的电流谐波畸变率)的探索
假如针对6次脉动的抑制并不是完全消除,而是和电流THD进行均衡呢?
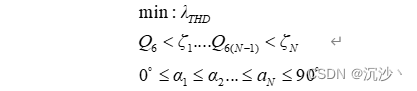
先把6次转矩波动的范围扩大一些,从0.001扩大到0.01;查看解集的变化;
%%%%%%%%%%%%%%%%%%%%%%%%%%%% 在图像上绘制5次和7次相等的曲线 %%%%%%%%%%%%%
% for i = 1:10
% 选择一些范围内的 x 和 y 值
clear
x_values = 0:0.01:1.57;
y_values = 0:0.01:1.57;% 初始化解的列表
solutions = [];
% 计算方程的左边与右边之间的差异,并判断是否小于一个很小的阈值
threshold = 0.01;for x = x_valuesfor y = y_valuesleft_side = (1 - 2*cos(5*x) + 2*cos(5*y))/25;right_side = (1 - 2*cos(7*x) + 2*cos(7*y))/49;if abs(left_side - right_side)< thresholdsolutions = [solutions; x, y]; % 添加解到解的列表中 endendend
% 提取解的 x 和 y 坐标
x_values = solutions(:, 1);
y_values = solutions(:, 2);
figure(1)
% 绘制图像
scatter(x_values*180/pi, y_values*180/pi,2,'m');
xlabel('x');
ylabel('y');
title('Distribution of Solutions');
grid on;
hold on%%%%%%%%%%%%%%%%%%%%%%%%%%%% 在图像上绘制调制度曲线 %%%%%%%%%%%%%
% for i = 1:10
% 选择一些范围内的 x 和 y 值
clear
x_values = 0:0.001:1.57;
y_values = 0:0.001:1.57;% 初始化解的列表
solutions = [];
m = 0.5;
% 计算方程的左边与右边之间的差异,并判断是否小于一个很小的阈值
threshold = 0.001;for x = x_valuesfor y = y_valuesleft_side = 1 - 2*cos(x) + 2*cos(y);right_side =m;if abs(left_side - right_side) < thresholdsolutions = [solutions; x, y]; % 添加解到解的列表中endendend
% 提取解的 x 和 y 坐标
x_values = solutions(:, 1);
y_values = solutions(:, 2);
figure(1)
% 绘制图像
scatter(x_values*180/pi, y_values*180/pi,1,'r');
xlabel('x');
ylabel('y');
title('Distribution of Solutions');
grid on;
hold on%%%%%%%%%%%%%%%%%%%%%%%%%% 绘制电流THD 2d 曲线 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 初始化解的列表
L = length(x_values);
for i = 1:Lx = x_values(i);y = y_values(i);%%%%%%%%%%%%%%%%%% 谐波电压标幺 %%%%%%%%%%%%%%%%%%%%%%%%%%%n =50;V1_pu = (1-2*cos(1*x)+ 2*cos(1*y))/1;for j = 1:nlow = 6*j-1;up = 6*j+1;Vlow_pu(j) = (1 - 2*cos(low*x) + 2*cos(low*y) )/low;Vup_pu(j) =(1 - 2*cos(up*x) + 2*cos(up*y) )/up;In(j) = abs(Vlow_pu(j)/low)^2 + abs(Vup_pu(j)/up)^2 ;Tn(j) = abs(Vlow_pu(j)/low - Vup_pu(j)/up) + 0*abs(Vlow_pu(j)/low + Vup_pu(j)/up); endF_Cthd(i) = sqrt(sum(In))/m;F_Ten(i) = sum(Tn); end% 绘制图像figure(3)
t= 1:1:L;
plot(F_Cthd);
xlabel('x');
ylabel('y');
hold on figure(3)
t= 1:1:L;
plot(F_Ten);
xlabel('x');
ylabel('y');
hold on [min_value, min_index] = min(F_Cthd)
disp(['电流THD最小的开关角a1:', num2str(x_values(min_index)*180/pi)]);
disp(['电流THD最小的开关角a2:', num2str(y_values(min_index)*180/pi)]);
disp(['电流THD为:', num2str(F_Cthd(min_index))]);
[min_value, min_index] = min(F_Ten)
disp(['转矩THD最小的开关角a1:', num2str(x_values(min_index)*180/pi)]);
disp(['转矩THD最小的开关角a2:', num2str(y_values(min_index)*180/pi)]);
disp(['转矩THD为:', num2str(F_Ten(min_index))]);
% alpha_a1 = x_values(351)*180/pi
% alpha_a2 = y_values(351)*180/pi脚本运行结果如下图所示:
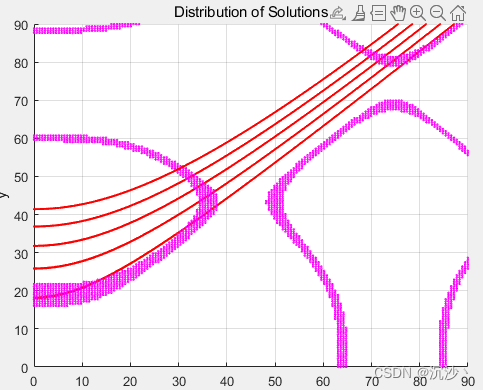
假如选择解集中电流THD最小的点作为开关角,即可实现在这个限幅值目标下电流THD的优化;可以试试这个效果;
针对这个公式:
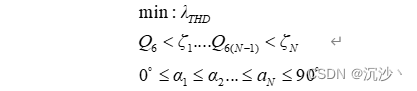
解算代码;
% alpha_init=[60*pi/180,90*pi/180]; %开关角初值给定 60-90°
alpha_init=[60*pi/180,90*pi/180]; %开关角初值给定 0-60°
t = 1:1:100;
L = length(t);
for i = 1:Lm = i /L;
A=[];b=[];Aeq=[];beq=[];lb=[];ub=[];
options=optimset('Display','none');
nonlcon=@(x)mycon(x,m);
[alpha_tmp,fval,exitflag]=fmincon(@(x)myfun(x),alpha_init,A,b,Aeq,beq,lb,ub,nonlcon,options);
alpha1_save(i) = alpha_tmp(1)*180/pi;
alpha2_save(i) = alpha_tmp(2)*180/pi;
alpha=alpha_tmp;
alpha=(180/pi)*alpha ; %弧度转换为角度
% figure(1)
% scatter(alpha(1),alpha(2),80,'filled');
hold on
end
figure(2)
plot(t/L,alpha1_save);
ylim([0, 90]);
hold on
plot(t/L,alpha2_save);
ylim([0, 90]);
hold on
alpha1_save(90)
alpha2_save(90)%%%%%%%%%%%% 电流THD 最小化目标 %%%%%%%%%%%%%
function F=myfun(x)
Uk_sum=0;
Qk_sum=0;
U1=1-2*cos(x(1))+2*cos(x(2));
sigma = 1;
for k=1:100Uk_1=( 1-2*cos((6*k-1)*x(1))+2*cos((6*k-1)*x(2)) )/(6*k-1);Uk_2=( 1-2*cos((6*k+1)*x(1))+2*cos((6*k+1)*x(2)) )/(6*k+1);Uk =(Uk_1/(6*k-1)/U1)^2+(Uk_2/(6*k+1)/U1)^2 ;Uk_sum=Uk+Uk_sum;endF=sigma*sqrt(Uk_sum);
endfunction [c,ceq]= mycon(x,t)%%%%%% 调制度约束 V1 = 1-2*cos(x(1))+2*cos(x(2));U1 = V1;ceq(1)= U1 - t;%%%%%% 开关角大小的约束 %%%%%%%%%c(1)=0/180*pi-x(1);c(2)=x(1)-x(2);c(3)=x(2)-pi/2;%%%%%% 转矩抑制 Q6 < 0.01 约束,注意等式要用 c V5 = ( 1-2*cos(5*x(1))+2*cos(5*x(2)) ) /5 ;V7 = ( 1-2*cos(7*x(1))+2*cos(7*x(2)) ) /7 ;Q6 = abs(V5/5 - V7/7);c(4) = Q6 - 0.01;end解算结果如下图所示;
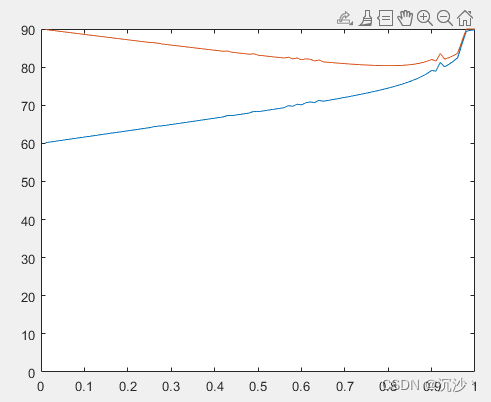
在调制度为0.9时刻进行仿真验证;此时求得的开关角为
a1 = 79.1114; a2 = 82.0158; 这个值和印度人那个方法解出来的值一摸一样;
尝试将范围放大;
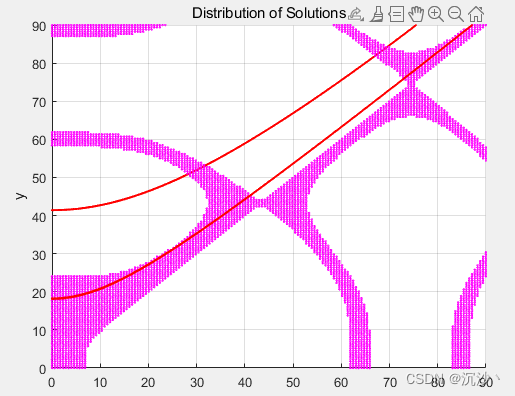
再次计算:
a1 = 78.4423; a2 = 81.3523; Q6=8.07;Tr = 12.42;THD=65.93
a1 = 79.1114; a2 = 82.0158; Q6=2.31;Tr = 11.47;THD=65.98;这个值和印度人那个方法解出来的;
从结果来看,有优化但是效果不是很大,可能是这个调制度恰好这个点就是THD比较小的,或许其他调制的效果更好一些;
测试在调制度为0.8的值;两者计算值一致;
测试在调制度为0.7的值;两者计算值一致;
测试在调制度为0.6的值;两者计算值一致;
测试在调制度为0.92的值;两者计算值不一致;
a1 = 79.4693; a2 = 81.7923; Q6=14.172;Tr = 10.43;THD=65.37
a1 = 81.2482; a2 = 83.5605; Q6=2.13 ;Tr = 8.362;THD=65.59 ;这个值和印度人那个方法解出来的;
从结果来看,有优化但是效果不是很大,可能是这个调制度恰好这个点就是THD比较小的,或许其他调制的效果更好一些;在低调制度区间没有很好的效果,按照印度人解算出来的值就是比较优选的方案。
这种设置限制大小的方式或者更适合没有解区间的调制度,即调制度在0.94 - 1之间时;
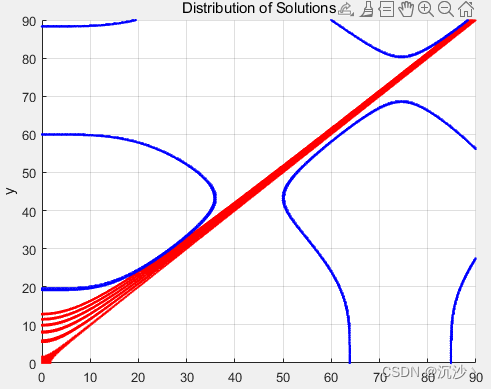
图中红色区域全是没有解的区间,在这个区间可以将6次转矩脉动的幅值放宽,这个宽度要正好覆盖这个区域。并且结合新的约束目标,整体的思想:

这个约束值就是包含 m=1的极限情况;
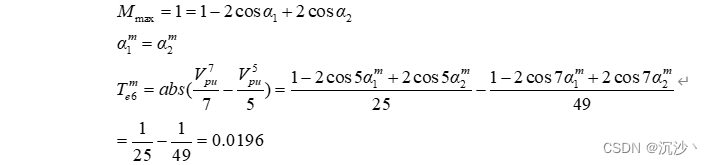
代码实现:
% alpha_init=[60*pi/180,90*pi/180]; %开关角初值给定 60-90°
alpha_init=[00*pi/180,60*pi/180]; %开关角初值给定 0-60°
t = 1:1:100;
L = length(t);
for i = 1:Lm = i /L;
A=[];b=[];Aeq=[];beq=[];lb=[];ub=[];
options=optimset('Display','none');
nonlcon=@(x)mycon(x,m);
[alpha_tmp,fval,exitflag]=fmincon(@(x)myfun(x),alpha_init,A,b,Aeq,beq,lb,ub,nonlcon,options);
alpha1_save(i) = alpha_tmp(1)*180/pi;
alpha2_save(i) = alpha_tmp(2)*180/pi;
alpha=alpha_tmp;
alpha=(180/pi)*alpha ; %弧度转换为角度
% figure(1)
% scatter(alpha(1),alpha(2),80,'filled');
hold on
end
figure(2)
plot(t/L,alpha1_save);
ylim([0, 90]);
hold on
plot(t/L,alpha2_save);
ylim([0, 90]);
hold on
alpha1_save(98)
alpha2_save(98)%%%%%%%%%%%% 电流THD 最小化目标 %%%%%%%%%%%%%
function F=myfun(x)
Uk_sum=0;
Qk_sum=0;
U1=1-2*cos(x(1))+2*cos(x(2));
sigma = 1;
for k=1:100Uk_1=( 1-2*cos((6*k-1)*x(1))+2*cos((6*k-1)*x(2)) )/(6*k-1);Uk_2=( 1-2*cos((6*k+1)*x(1))+2*cos((6*k+1)*x(2)) )/(6*k+1);Uk =(Uk_1/(6*k-1)/U1)^2+(Uk_2/(6*k+1)/U1)^2 ;Uk_sum=Uk+Uk_sum;endF=sigma*sqrt(Uk_sum);
endfunction [c,ceq]= mycon(x,t)%%%%%% 调制度约束 V1 = 1-2*cos(x(1))+2*cos(x(2));U1 = V1;ceq(1)= U1 - t;%%%%%% 开关角大小的约束 %%%%%%%%%c(1)=0/180*pi-x(1);c(2)=x(1)-x(2);c(3)=x(2)-pi/2;if t>0.94V5 = ( 1-2*cos(5*x(1))+2*cos(5*x(2)) ) /5 ;V7 = ( 1-2*cos(7*x(1))+2*cos(7*x(2)) ) /7 ;Q6 = abs(V5/5 - V7/7);c(4) = Q6 - 0.02;elseV5 = ( 1-2*cos(5*x(1))+2*cos(5*x(2)) ) /5 ;V7 = ( 1-2*cos(7*x(1))+2*cos(7*x(2)) ) /7 ;Q6 = abs(V5/5 - V7/7);ceq(2) =0- Q6;endend进行仿真复现,开关角解算结果;
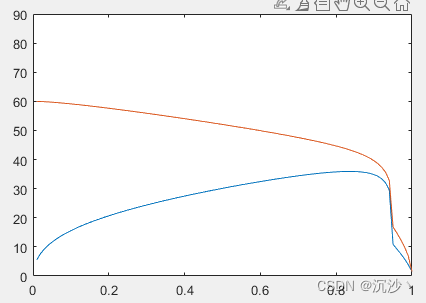
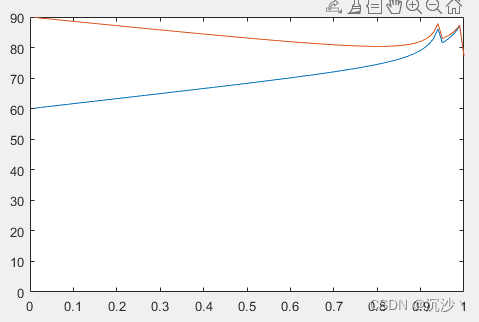
原始论文的结果;
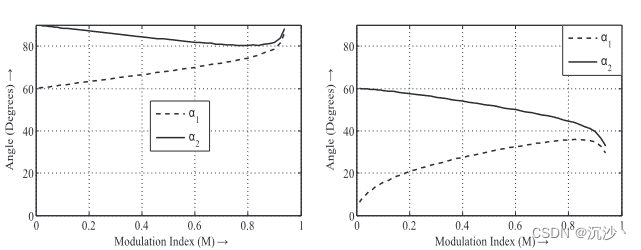
这是利用THD的方法进行解决的;但是这里有个东西站不住,就是覆盖的范围内的电流THD求最优是否就等价于CHMPWM了呢?至少在开关角等于2的时候,完全是包含的关系。开关角等于3和等于4的时候就不一定了,这个需要证明一下。
另一条路径:
那么能否利用更加优选的,时刻保持最优Q6的方式解决呢?
那么实际上是寻优的过程,整体思想为:
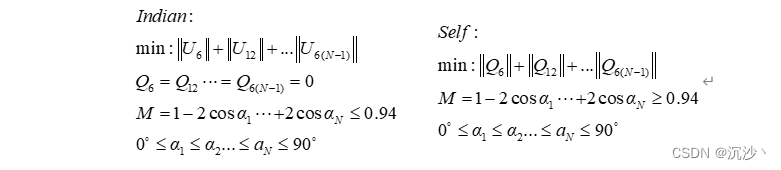
执行代码:
% alpha_init=[60*pi/180,90*pi/180]; %开关角初值给定 60-90°
alpha_init=[0*pi/180,60*pi/180]; %开关角初值给定 0-60°
t = 1:1:100;
L = length(t);
for i = 1:Lm = i /L;
A=[];b=[];Aeq=[];beq=[];lb=[];ub=[];
options=optimset('Display','none');
nonlcon=@(x)mycon(x,m);
[alpha_tmp,fval,exitflag]=fmincon(@(x)myfun(x),alpha_init,A,b,Aeq,beq,lb,ub,nonlcon,options);
alpha1_save(i) = alpha_tmp(1)*180/pi;
alpha2_save(i) = alpha_tmp(2)*180/pi;
alpha=alpha_tmp;
alpha=(180/pi)*alpha ; %弧度转换为角度
% figure(1)
% scatter(alpha(1),alpha(2),80,'filled');
hold on
end
figure(2)
plot(t/L,alpha1_save);
ylim([0, 90]);
hold on
plot(t/L,alpha2_save);
ylim([0, 90]);
hold on
alpha1_save(96)
alpha2_save(96)%%%%%%%%%%%% 电流THD 最小化目标 %%%%%%%%%%%%%
function F=myfun(x)V5 = ( 1-2*cos(5*x(1))+2*cos(5*x(2)) ) /5 ;V7 = ( 1-2*cos(7*x(1))+2*cos(7*x(2)) ) /7 ;Q6 = abs(V5/5 - V7/7);
% U6 = abs(V5/5 + V7/7);% F=Q6+U6;F = Q6;
endfunction [c,ceq]= mycon(x,t)%%%%%% 调制度约束 V1 = 1-2*cos(x(1))+2*cos(x(2));U1 = V1;ceq(1)= U1 - t;%%%%%% 开关角大小的约束 %%%%%%%%%c(1)=0/180*pi-x(1);c(2)=x(1)-x(2);c(3)=x(2)-pi/3;end仿真验证,是不是时刻保证最优的Q6的;把集中方法对比一下,其数据如下图所示:
(1)THDMIN+ 转矩波动限制的0.02时 : Tr = 8.2 THD 36.8 6次转矩分量为67.63
(2)THDMIN+加了转矩波动限制的0.01时 : Tr = 6.053 THD 60.25 6次转矩分量为46.11
(2) Q6最小 %: Tr = 6.132 THD 62.63 6 次转矩分量为50.77

3.2 针对局限性2:(6次转矩脉动的抑制,整体转矩振荡幅值增大)的探索
假如优化的目标不再是针对6次转矩脉动的抑制,而是整体转矩振荡幅值最小呢?
4 应用遍历思想的探索
在应用fmincon函数的过程中,一直都存在初值设置不准的问题,不同的初值设置,得到的结果完全不相同。为了能够得到更为直接的结果,且不受到初值的影响,探索应用遍历的方法对所有角度的信息进行求解。
4.1 目标函数为电流THD,求其最小值;
公式原理:
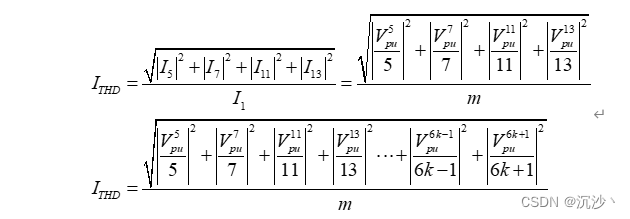
求解CHMPWM开关角代码;全部调制度的求解,并保存开关角;
% 定义函数 0.9 = 1 - 2*cos(x) + 2*cos(y)
% 通过重排可以得到 2*cos(y) = 0.1 + 2*cos(x)
% 解出 y
% y = acos(0.1/2 + cos(x))% 创建一系列 x 值
m_div = 1000;
t = 1:1:m_div;
for a = 1:m_divm = a /m_divx_values = linspace(0, pi/2, 10000);% 计算对应的 y 值y_values = acos((1-m)/2 + cos(x_values));%%%%%%%%%%%对求解结果的非实数解进行去除 %%%%%%%%%%%%%L = length(y_values);for i=1:Lis_z_real = isreal(y_values(i));if is_z_real == 0y_values(i) = 0;end endalpha1 = y_values(2020:10000);
alpha2 = x_values(2020:10000);% figure(1)
% 绘制 y 关于 x 的图像
% plot(alpha1*180/pi, alpha2*180/pi,'linewidth',5);
% xlabel('a1');
% ylabel('a2');
% title('a2 关于 a1 的函数图像');
% hold on %%%%%%%%%%%%%%%%%%%%%%%%%% 绘制电流THD 2d 曲线 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 初始化解的列表
L_in = length(alpha1);for i = 1:L_inx = alpha1(i);y = alpha2(i);%%%%%%%%%%%%%%%%%% 谐波电压标幺 %%%%%%%%%%%%%%%%%%%%%%%%%%%n =50;V1_pu = (1-2*cos(1*x)+ 2*cos(1*y))/1;for j = 1:nlow = 6*j-1;up = 6*j+1;Vlow_pu(j) = (1 - 2*cos(low*x) + 2*cos(low*y) )/low; % 6k-1次数电压Vup_pu(j) =(1 - 2*cos(up*x) + 2*cos(up*y) )/up; % 6k+1次数电压In(j) = abs(Vlow_pu(j)/low)^2 + abs(Vup_pu(j)/up)^2 ;% 6k-+1次电流 endF_Cthd(i) = sqrt(sum(In))/m;% 然后所有的平方和 ,开方,除以调制度 end
[min_value, min_index] = min(F_Cthd);
% disp(['电流THD最小的开关角a1:', num2str(alpha1(min_index)*180/pi)]);
% disp(['电流THD最小的开关角a2:', num2str(alpha2(min_index)*180/pi)]);
% disp(['电流THD为:', num2str(F_Cthd(min_index))]);
alpha1_out(a) = alpha1(min_index);
alpha2_out(a) = alpha2(min_index);
F_Cthd_out(a) = min(F_Cthd);
end
figure(2)
t = 1:1:m_div;
plot(t/m_div,alpha1_out*180/pi);
hold on
plot(t/m_div,alpha2_out*180/pi);
hold on
figure(3)
plot(t/m_div,F_Cthd_out);
hold on %
% figure
% t= 1:1:L;
% plot(F_Cthd);
% xlabel('x');
% ylabel('y');
% hold on 4.2 目标函数为转矩THD,求其最小值;
定点的M,时变的m还没调通;
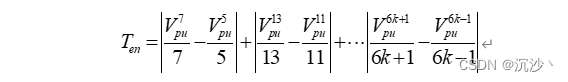
对上式进行编程求解:
% 定义函数 0.9 = 1 - 2*cos(x) + 2*cos(y)
% 通过重排可以得到 2*cos(y) = 0.1 + 2*cos(x)
% 解出 y
% y = acos(0.1/2 + cos(x))% 创建一系列 x 值
clear m = 0.9;x_values = linspace(0, pi/2, 10000);% 计算对应的 y 值y_values = acos((1-m)/2 + cos(x_values));%%%%%%%%%%%对求解结果的非实数解进行去除 %%%%%%%%%%%%%L = length(y_values);for i=1:Lis_z_real = isreal(y_values(i));if is_z_real == 0y_values(i) = 0;end endalpha1 = y_values(2020:10000);
alpha2 = x_values(2020:10000);% figure(1)
% 绘制 y 关于 x 的图像
% plot(alpha1*180/pi, alpha2*180/pi,'linewidth',5);
% xlabel('a1');
% ylabel('a2');
% title('a2 关于 a1 的函数图像');
% hold on %%%%%%%%%%%%%%%%%%%%%%%%%% 绘制电流THD 2d 曲线 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 初始化解的列表
L_in = length(alpha1);for i = 1:L_inx = alpha1(i);y = alpha2(i);%%%%%%%%%%%%%%%%%% 谐波电压标幺 %%%%%%%%%%%%%%%%%%%%%%%%%%%n =50;V1_pu = (1-2*cos(1*x)+ 2*cos(1*y))/1;for j = 1:nlow = 6*j-1;up = 6*j+1;Vlow_pu(j) = (1 - 2*cos(low*x) + 2*cos(low*y) )/low; % 6k-1次数电压Vup_pu(j) =(1 - 2*cos(up*x) + 2*cos(up*y) )/up; % 6k+1次数电压In(j) = abs(Vlow_pu(j)/low)^2 + abs(Vup_pu(j)/up)^2 ;% 6k-+1次电流 Tn(j) = abs( Vlow_pu(j)/low - Vup_pu(j)/up) + 0*abs(Vlow_pu(j)/low + Vup_pu(j)/up); endF_Cthd(i) = sqrt(sum(In))/m;% 然后所有的平方和 ,开方,除以调制度 F_Ten(i) = sum(Tn); endfigure(1);plot(F_Ten)%%%%%%%%%%%%%%%% 电流求THD最小 %%%%%%%%%%%%%%%%%%%%
[min_value, min_index] = min(F_Cthd);
% disp(['电流THD最小的开关角a1:', num2str(alpha1(min_index)*180/pi)]);
% disp(['电流THD最小的开关角a2:', num2str(alpha2(min_index)*180/pi)]);
% disp(['电流THD为:', num2str(F_Cthd(min_index))]);
alpha1_THD = alpha1(min_index);
alpha2_THD = alpha2(min_index);
F_Cthd_out = min(F_Cthd);%%%%%%%%%%%%%%%% 转矩求THD最小 %%%%%%%%%%%%%%%%%%%%
[min_value, min_index] = min( F_Ten)
disp(['转矩THD最小的开关角a1:', num2str(alpha1(min_index)*180/pi)]);
disp(['转矩THD最小的开关角a2:', num2str(alpha2(min_index)*180/pi)]);
disp(['转矩THD为:', num2str(F_Cthd(min_index))]);
alpha1_Tr = alpha1(min_index);
alpha2_Tr = alpha2(min_index);
F_Ten_Tr = min( F_Ten);此时输出转矩THD波形如下所示:
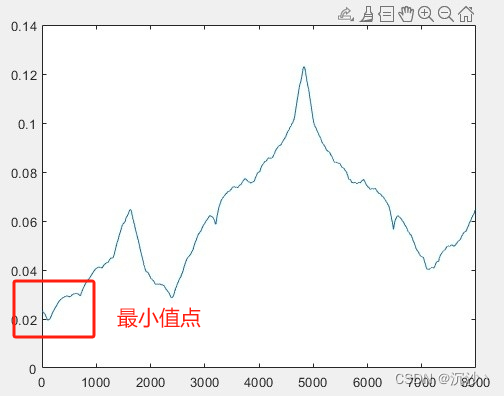
matlab的指令行输出如下所示:
代入解算结果中的几个点仿真试一下;
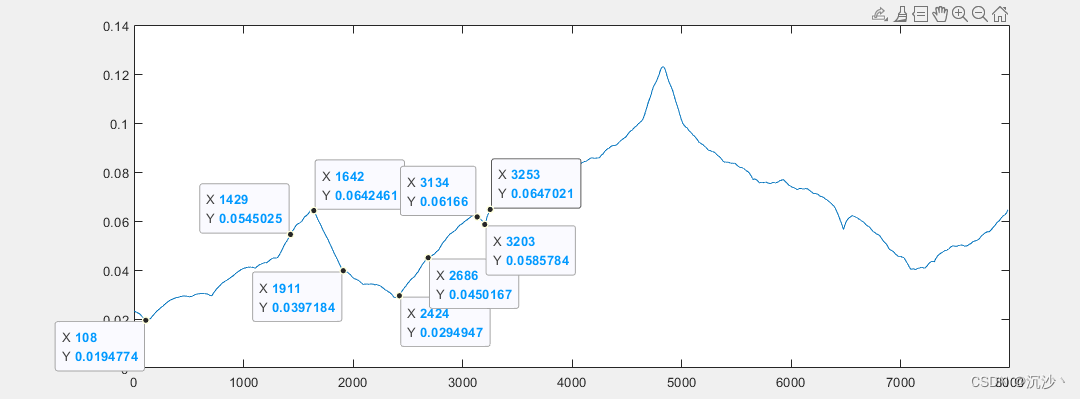
%%%%%%%%%%%% 108 %%%%%%%%%%%% Tr = 7.47 THD 94.31
% %%%%%%%%%%%% 711 %%%%%%%%%%%% Tr = 10.83 THD 64.92
%%%%%%%%%%%% 1429 %%%%%%%%%%%% Tr = 17.68 THD 67.06
%%%%%%%%%%%% 1642 %%%%%%%%%%%% Tr = 19.51 THD 72.82
%%%%%%%%%%%% 1911 %%%%%%%%%%%% Tr = 14.57 THD 86.58
%%%%%%%%%%%% 2424 %%%%%%%%%%%% Tr = 10.19 THD 104.31
%%%%%%%%%%%% 2686 %%%%%%%%%%%% Tr = 14.26 THD 109.77
%%%%%%%%%%%% 3134 %%%%%%%%%%%% Tr = 20.07 THD 114.62
%%%%%%%%%%%% 3203%%%%%%%%%%%% Tr = 20.87 THD 115.67
%%%%%%%%%%%% 3253 %%%%%%%%%%%% Tr = 21.66 THD 115.98
这些数据基本是按照遍历出来的结果显示的。