矩阵分解的方法也分为很多种:SVD、LFM、BiasSVD和SVD++。
- Traditional SVD
一般SVD矩阵分解指的是SVD奇异值分解,将矩阵分解成三个相乘矩阵,中间矩阵就是奇异值矩阵。SVD分解的前提是矩阵是稠密的,现实场景中数据都是稀疏的,无法使用SVD,需要均值或者其他方法来填充,会对数据造成一定影响。具体公式如下:
M m × n = U m × k ∑ k × k K k × n T M_{m×n} = U_{m×k}\sum_{k×k}K^T_{k×n} Mm×n=Um×k∑k×kKk×nT - FunkSVD(LFM)
FunkSVD是最原始的LFM模型,它将矩阵分解为2个矩阵:用户-隐含特征矩阵,物品-隐含特征矩阵,一般这个过程跟线性回归类似。以下公式为矩阵分解后的损失函数,p为用户-隐含特征矩阵,q为物品-隐含特征矩阵,我们通过求损失函数的最小值来计算p和q,后面部分为L2范式,防止过拟合。下面公式用随机梯度下降来求最优解。
m i n q p ∑ ( u , i ) ∈ R ( r u i − q i T p u ) 2 + λ ( ∣ ∣ q i ∣ ∣ 2 + ∣ ∣ p u ∣ ∣ 2 ) \mathop{min}\limits_{qp}\sum_{(u,i)∈R}(r_{ui}-q^T_ip_u)^2+\lambda(||q_i||^2+||p_u||^2) qpmin(u,i)∈R∑(rui−qiTpu)2+λ(∣∣qi∣∣2+∣∣pu∣∣2) - BiasSVD
BiasSVD就是在FunkSVD的基础上加上Baseline基准预测的偏置项,具体公式如下:
m i n q p ∑ ( u , i ) ∈ R ( r u i − u − b u − b i − q i T p u ) 2 + λ ( ∣ ∣ q i ∣ ∣ 2 + ∣ ∣ p u ∣ ∣ 2 + ∣ ∣ b u ∣ ∣ 2 + ∣ ∣ b i ∣ ∣ 2 ) \mathop{min}\limits_{qp}\sum_{(u,i)∈R}(r_{ui}-u-b_u-b_i-q^T_ip_u)^2+\lambda(||q_i||^2+||p_u||^2+||b_u||^2+||b_i||^2) qpmin(u,i)∈R∑(rui−u−bu−bi−qiTpu)2+λ(∣∣qi∣∣2+∣∣pu∣∣2+∣∣bu∣∣2+∣∣bi∣∣2) - SVD++
改进的BiasSVD,即在BiasSVD的基础上再加上用户的隐式反馈信息。这里不做多介绍。
1 LFM原理解析
LFM隐语义模型的核心思想是通过隐含特征联系用户和物品。
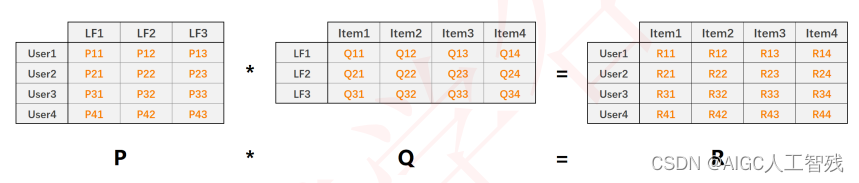
P是用户和隐含特征矩阵,这里表示三个隐含特征;
Q是隐含特征和物品矩阵
Q是User-Item,由P*Q得来。
我们利用矩阵分解技术,将User-Item评分矩阵分解为P和Q的矩阵,然后利用P*Q还原评分矩阵。其中 R 11 = P 1 , k ⃗ ⋅ Q k , 1 ⃗ R_{11} = \vec{P_{1,k}}·\vec{Q_{k,1}} R11=P1,k⋅Qk,1
所以我们的评分为:
r u i ^ = p u , k ⃗ ⋅ q i , k ⃗ = ∑ k = 1 k p u k q i k \hat{r_{ui}} = \vec{p_{u,k}}·\vec{q_{i,k}} = \sum_{k=1}^{k}p_{uk}q_{ik} rui^=pu,k⋅qi,k=k=1∑kpukqik
损失函数
C o s t = ∑ u , i ∈ R ( r u i − r ^ u i ) 2 = ∑ u , i ∈ R ( r u i − ∑ k = 1 k p u k q i k ) 2 Cost = \sum_{u,i∈R}(r_{ui}-\hat r_{ui})^2 = \sum_{u,i∈R}(r_{ui}-\sum_{k=1}^{k}p_{uk}q_{ik})^2 Cost=u,i∈R∑(rui−r^ui)2=u,i∈R∑(rui−k=1∑kpukqik)2
加入L2范式防止过拟合,如下:
C o s t = ∑ u , i ∈ R ( r u i − ∑ k = 1 k p u k q i k ) 2 + λ ( ∑ U p u k 2 + ∑ I q i k 2 ) Cost = \sum_{u,i∈R}(r_{ui}-\sum_{k=1}^{k}p_{uk}q_{ik})^2 +\lambda(\sum_U p^2_{uk}+\sum_I q^2_{ik}) Cost=u,i∈R∑(rui−k=1∑kpukqik)2+λ(U∑puk2+I∑qik2)
对损失函数求偏导可得:
∂ ∂ p u k C o s t = 2 ∑ u , i ∈ R ( r u i − ∑ k = 1 k p u k q i k ) ( − q i k ) + 2 λ p u k \frac{∂}{∂p_{uk}}Cost = 2\sum_{u,i∈R}(r_{ui}-\sum_{k=1}^{k}p_{uk}q_{ik})(-q_{ik}) + 2\lambda p_{uk} ∂puk∂Cost=2u,i∈R∑(rui−k=1∑kpukqik)(−qik)+2λpuk
∂ ∂ q i k C o s t = 2 ∑ u , i ∈ R ( r u i − ∑ k = 1 k p u k q i k ) ( − p u k ) + 2 λ q i k \frac{∂}{∂q_{ik}}Cost = 2\sum_{u,i∈R}(r_{ui}-\sum_{k=1}^{k}p_{uk}q_{ik})(-p_{uk}) + 2\lambda q_{ik} ∂qik∂Cost=2u,i∈R∑(rui−k=1∑kpukqik)(−puk)+2λqik
随机梯度下降法优化
根据偏导可更新梯度下降参数:
p u k : = p u k + α [ ∑ u , i ∈ R ( r u i − ∑ k = 1 k p u k q i k ) ( q i k ) − λ 1 p u k ] p_{uk}:=p_{uk} + \alpha[\sum_{u,i∈R}(r_{ui}-\sum_{k=1}^{k}p_{uk}q_{ik})(q_{ik}) - \lambda_1 p_{uk}] puk:=puk+α[u,i∈R∑(rui−k=1∑kpukqik)(qik)−λ1puk]
q i k : = p i k + α [ ∑ u , i ∈ R ( r u i − ∑ k = 1 k p u k q i k ) ( p u k ) − λ 2 q i k ] q_{ik}:=p_{ik} + \alpha[\sum_{u,i∈R}(r_{ui}-\sum_{k=1}^{k}p_{uk}q_{ik})(p_{uk}) -\lambda_2 q_{ik}] qik:=pik+α[u,i∈R∑(rui−k=1∑kpukqik)(puk)−λ2qik]
随机梯度下降:
应用到每个向量里
p u k : = p u k + α [ ( r u i − ∑ k = 1 k p u k q i k ) ( q i k ) − λ 1 p u k ] p_{uk}:=p_{uk} + \alpha[(r_{ui}-\sum_{k=1}^{k}p_{uk}q_{ik})(q_{ik}) - \lambda_1 p_{uk}] puk:=puk+α[(rui−k=1∑kpukqik)(qik)−λ1puk]
q i k : = p i k + α [ ( r u i − ∑ k = 1 k p u k q i k ) ( p u k ) − λ 2 q i k ] q_{ik}:=p_{ik} + \alpha[(r_{ui}-\sum_{k=1}^{k}p_{uk}q_{ik})(p_{uk}) -\lambda_2 q_{ik}] qik:=pik+α[(rui−k=1∑kpukqik)(puk)−λ2qik]
算法实现
这里只展示LFM算法的代码,数据集分割代码和评估代码见:大数据——协同过滤推荐算法:线性回归算法
# FunkSVD
class LFM(object):'''max_epochs 梯度下降迭代次数alpha 学习率reg 过拟合参数columns 数据字段名称'''def __init__(self,max_epochs,p_reg,q_reg,alpha,number_LatentFactors=30,columns=['userId','movieId','rating']):self.max_epochs = max_epochsself.p_reg = p_regself.q_reg = q_regself.number_LatentFactors=number_LatentFactors #隐式特征的数量self.alpha = alphaself.columns = columnsdef fit(self,data):''':param data:uid,mid,rating:return:'''self.data = data# 用户评分数据self.users_rating = data.groupby(self.columns[0]).agg([list])[[self.columns[1], self.columns[2]]]# 电影评分数据self.items_rating = data.groupby(self.columns[1]).agg([list])[[self.columns[0], self.columns[2]]]# 全局平均分self.global_mean = self.data[self.columns[2]].mean()# 调用随机梯度下降训练模型参数self.p,self.q = self.sgd()def _init_matrix(self):# 构建p的矩阵,其中第二项元素的大小为用户数量*隐式特征p = dict(zip(self.users_rating.index, np.random.rand(len(self.users_rating), self.number_LatentFactors).astype(np.float32)))# 构建q的矩阵,其中第二项元素的大小为物品数量*隐式特征q = dict(zip(self.items_rating.index,np.random.rand(len(self.items_rating), self.number_LatentFactors).astype(np.float32)))return p,qdef sgd(self):'''最小二乘法,优化q和p值:return: q p'''p,q = self._init_matrix()for i in range(self.max_epochs):error_list = []for uid,mid,r_ui in self.data.itertuples(index=False):# user-lf p# item-lf qv_pu = p[uid]v_qi = q[mid]err = np.float32(r_ui - np.dot(v_pu, v_qi))v_pu += self.alpha*(err*v_qi - self.p_reg*v_pu)v_qi += self.alpha*(err*v_pu - self.q_reg*v_qi)p[uid] = v_puq[mid] = v_qierror_list.append(err**2)return p,qdef predict(self,uid,mid):'''使用评分公式进行预测param uid,mid;return predict_rating;'''if uid not in self.users_rating.index or mid not in self.items_rating.index:return self.global_meanp_u = self.p[uid]q_i = self.q[mid]return np.dot(p_u,q_i)def test(self,testset):'''使用预测函数预测测试集数据param testset;return yield;'''for uid,mid,real_rating in testset.itertuples(index=False):try:# 使用predict函数进行预测pred_rating = self.predict(uid,mid)except Exception as e:print(e)else:# 返回生成器对象yield uid,mid,real_rating,pred_rating测试LFM算法
trainset, testset = data_split('ml-latest-small/ratings.csv',random=True)
lfm = LFM(100,0.01,0.01,0.02,10,['userId','movieId','rating'])
lfm.fit(trainset)
pred_test = lfm.test(testset)
# 生成器对象用list进行转化,然后转化为dataframe格式
df_pred_LFM = pd.DataFrame(list(pred_test), columns=[['userId','movieId','rating','pred_rating']])
rmse, mae = accuray(df_pred_als,'all')
print('rmse:',rmse,';mae:',mae)
rmse: 1.0718 ;mae: 0.8067
2 BiasSVD原理
BiasSVD是在FunkSVD矩阵分解的基础上加上了偏置项的。评分公式如下:
r ^ u i = u + b u + b i + p u k ⃗ ⋅ q k i ⃗ = u + b u + b i + ∑ k = 1 k p u k ⋅ q k i \hat r_{ui} = u+b_u+b_i+\vec{p_{uk}}·\vec{q_{ki}} = u+b_u+b_i+\sum^{k}_{k=1}{p_{uk}}·{q_{ki}} r^ui=u+bu+bi+puk⋅qki=u+bu+bi+k=1∑kpuk⋅qki
损失函数
C o s t = ∑ u , i ∈ R ( r u i − r ^ u i ) 2 = ∑ u , i ∈ R ( r u i − u − b u − b i − ∑ k = 1 k p u k ⋅ q k i ) 2 Cost = \sum_{u,i∈R}(r_{ui}-\hat r_{ui})^2 = \sum_{u,i∈R}(r_{ui}-u-b_u-b_i-\sum^{k}_{k=1}{p_{uk}}·{q_{ki}})^2 Cost=u,i∈R∑(rui−r^ui)2=u,i∈R∑(rui−u−bu−bi−k=1∑kpuk⋅qki)2
加入L2范式
C o s t = ∑ u , i ∈ R ( r u i − r ^ u i ) 2 = ∑ u , i ∈ R ( r u i − u − b u − b i − ∑ k = 1 k p u k ⋅ q k i ) 2 + λ ( ∑ U b u 2 + ∑ I b i 2 + ∑ U p u k 2 + ∑ I q i k 2 ) Cost = \sum_{u,i∈R}(r_{ui}-\hat r_{ui})^2 = \sum_{u,i∈R}(r_{ui}-u-b_u-b_i-\sum^{k}_{k=1}{p_{uk}}·{q_{ki}})^2 +\lambda(\sum_Ub^2_u+\sum_Ib^2_i+\sum_Up^2_{uk}+\sum_Iq^2_{ik}) Cost=u,i∈R∑(rui−r^ui)2=u,i∈R∑(rui−u−bu−bi−k=1∑kpuk⋅qki)2+λ(U∑bu2+I∑bi2+U∑puk2+I∑qik2)
随机梯度下降法优化
梯度下降更新参数:
p u k : = p u k + α [ ( r u i − u − b u − b i − ∑ k = 1 k p u k ⋅ q k i ) q i k − λ 1 p u k ] p_{uk}:=p_{uk} + \alpha[(r_{ui}-u-b_u-b_i-\sum^{k}_{k=1}{p_{uk}}·{q_{ki}})q_{ik}-\lambda_1p_{uk}] puk:=puk+α[(rui−u−bu−bi−k=1∑kpuk⋅qki)qik−λ1puk]
q i k : = p i k + α [ ( r u i − u − b u − b i − ∑ k = 1 k p u k ⋅ q k i ) p u k − λ 2 q i k ] q_{ik}:=p_{ik} + \alpha[(r_{ui}-u-b_u-b_i-\sum^{k}_{k=1}{p_{uk}}·{q_{ki}})p_{uk}-\lambda_2q_{ik}] qik:=pik+α[(rui−u−bu−bi−k=1∑kpuk⋅qki)puk−λ2qik]
b u : = b u + α [ ( r u i − u − b u − b i − ∑ k = 1 k p u k ⋅ q k i ) − λ 3 b u ] b_{u}:=b_{u} + \alpha[(r_{ui}-u-b_u-b_i-\sum^{k}_{k=1}{p_{uk}}·{q_{ki}})-\lambda_3b_{u}] bu:=bu+α[(rui−u−bu−bi−k=1∑kpuk⋅qki)−λ3bu]
b i : = b i + α [ ( r u i − u − b u − b i − ∑ k = 1 k p u k ⋅ q k i ) − λ 4 b i ] b_{i}:=b_{i} + \alpha[(r_{ui}-u-b_u-b_i-\sum^{k}_{k=1}{p_{uk}}·{q_{ki}})-\lambda_4b_{i}] bi:=bi+α[(rui−u−bu−bi−k=1∑kpuk⋅qki)−λ4bi]
算法实现
# BiasSVD
class BiasSvd(object):'''max_epochs 梯度下降迭代次数alpha 学习率reg 过拟合参数columns 数据字段名称'''def __init__(self,alpha,p_reg,q_reg,bu_reg,bi_reg,number_LatentFactors=10,max_epochs=10,columns=['userId','movieId','rating']):self.max_epochs = max_epochsself.p_reg = p_regself.q_reg = q_regself.bu_reg = bu_regself.bi_reg = bi_regself.number_LatentFactors=number_LatentFactors #隐式特征的数量self.alpha = alphaself.columns = columnsdef fit(self,data):''':param data:uid,mid,rating:return:'''self.data = data# 用户评分数据self.users_rating = data.groupby(self.columns[0]).agg([list])[[self.columns[1], self.columns[2]]]# 电影评分数据self.items_rating = data.groupby(self.columns[1]).agg([list])[[self.columns[0], self.columns[2]]]# 全局平均分self.global_mean = self.data[self.columns[2]].mean()# 调用随机梯度下降训练模型参数self.p,self.q, self.bu,self.bi= self.sgd()def _init_matrix(self):# 构建p的矩阵,其中第二项元素的大小为用户数量*隐式特征p = dict(zip(self.users_rating.index, np.random.rand(len(self.users_rating), self.number_LatentFactors).astype(np.float32)))# 构建q的矩阵,其中第二项元素的大小为物品数量*隐式特征q = dict(zip(self.items_rating.index,np.random.rand(len(self.items_rating), self.number_LatentFactors).astype(np.float32)))return p,qdef sgd(self):'''随机梯度下降,优化q和p值:return: q p'''p,q = self._init_matrix()bu = dict(zip(self.users_rating.index, np.zeros(len(self.users_rating))))bi = dict(zip(self.items_rating.index,np.zeros(len(self.items_rating))))for i in range(self.max_epochs):error_list = []for uid,mid,r_ui in self.data.itertuples(index=False):# user-lf p# item-lf qv_pu = p[uid]v_qi = q[mid]err = np.float32(r_ui - self.global_mean - bu[uid] - bi[mid]-np.dot(v_pu, v_qi))v_pu += self.alpha*(err*v_qi - self.p_reg*v_pu)v_qi += self.alpha*(err*v_pu - self.q_reg*v_qi)p[uid] = v_puq[mid] = v_qibu[uid] += self.alpha*(err - self.bu_reg*bu[uid])bi[mid] += self.alpha*(err - self.bi_reg*bi[mid])error_list.append(err**2)return p,q,bu,bidef predict(self,uid,mid):'''使用评分公式进行预测param uid,mid;return predict_rating;'''if uid not in self.users_rating.index or mid not in self.items_rating.index:return self.global_meanp_u = self.p[uid]q_i = self.q[mid]return self.global_mean+self.bu[uid]+self.bi[mid]+np.dot(p_u,q_i)def test(self,testset):'''使用预测函数预测测试集数据param testset;return yield;'''for uid,mid,real_rating in testset.itertuples(index=False):try:# 使用predict函数进行预测pred_rating = self.predict(uid,mid)except Exception as e:print(e)else:# 返回生成器对象yield uid,mid,real_rating,pred_rating算法使用
trainset, testset = data_split('ml-latest-small/ratings.csv',random=True)
bsvd = BiasSvd(0.02,0.01,0.01,0.01,0.01,10,20,['userId','movieId','rating'])
bsvd.fit(trainset)
pred_test = bsvd.test(testset)
# 生成器对象用list进行转化,然后转化为dataframe格式
df_pred_LFM = pd.DataFrame(list(pred_test), columns=[['userId','movieId','rating','pred_rating']])
rmse, mae = accuray(df_pred_als,'all')
print('rmse:',rmse,';mae:',mae)
rmse: 1.0718 ;mae: 0.8067