目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
- 5.代码获取
1.背景
2024年,J Lian受到人类进化启发,提出了人类进化优化算法(Human Evolutionary Optimization Algorithm, HEOA)。


2.算法原理
2.1算法思想
HEOA将全局搜索过程分为:人类探索和人类发展。初始化采用Logistic混沌映射,在人类探索阶段,进行初始的全局搜索。在人类发展阶段,人口被分类为领导者、探索者、追随者和失败者,每个人都使用不同的搜索策略。

2.2算法过程
人类探索阶段
探索阶段被定义为最大迭代次数的初始1/4。在人类发展的各个阶段,当面对未开发的领域和有限的知识时,个体倾向于采用统一的搜索策略:
X i t + 1 = β ⋅ ( 1 − t M a x i t e r ) ⋅ ( X i t − X b e s t ) ⋅ L e v y ( d i m ) + X b e s t ⋅ ( 1 − t M a x i t e r ) + ( X m e a n t − X b e s t ) ⋅ f l o o r ( r a n d f j u m p ) ⋅ f j u m p (1) X_{i}^{t+1}=\beta\cdot(1-\frac{t}{Max_{iter}})\cdot(X_{i}^{t}-X_{best})\cdot Levy(dim)+X_{best}\cdot(1-\frac{t}{Max_{iter}})+(X_{mean}^{t}-X_{best})\cdot floor(\frac{rand}{f_{jump}})\cdot f_{jump}\tag{1} Xit+1=β⋅(1−Maxitert)⋅(Xit−Xbest)⋅Levy(dim)+Xbest⋅(1−Maxitert)+(Xmeant−Xbest)⋅floor(fjumprand)⋅fjump(1)
其中, β \beta β为自适应因子,平均位置Xmean表述为:
X m e a n t = 1 N ∑ k = 1 N X k t (2) X_{mean}^t=\frac1N\sum_{k=1}^NX_k^t\tag{2} Xmeant=N1k=1∑NXkt(2)
自适应因子解释了人类探索知识的难度越来越大和群体特征:
β = 0.2 ( 1 − t M a x t e r ) ⋅ ( X i t − X m e a n t ) (3) \beta=0.2\Bigg(1-\frac t{Max_{ter}}\Bigg)\cdot\Bigg(X_i^t-X_{mean}^t\Bigg)\tag{3} β=0.2(1−Maxtert)⋅(Xit−Xmeant)(3)
跳跃策略
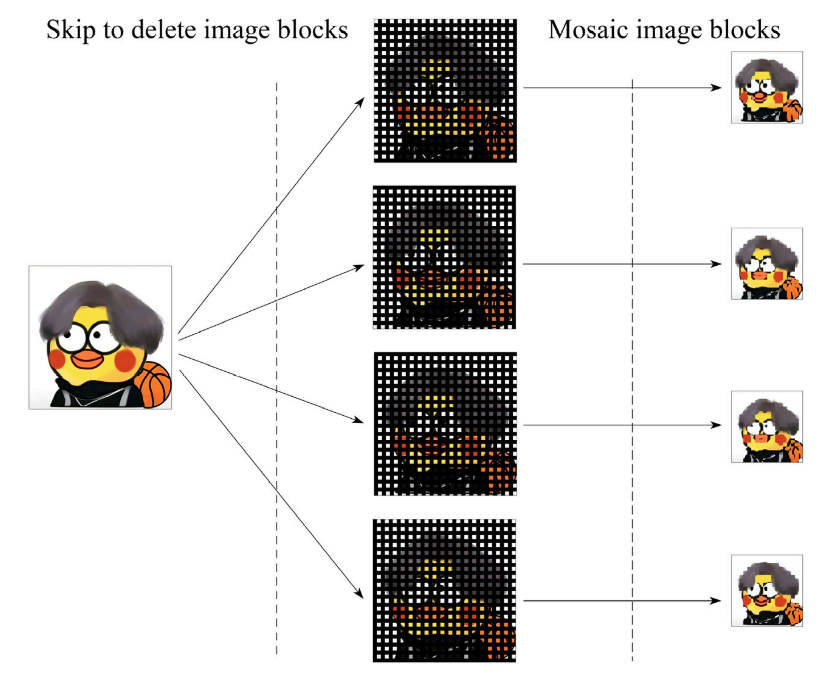
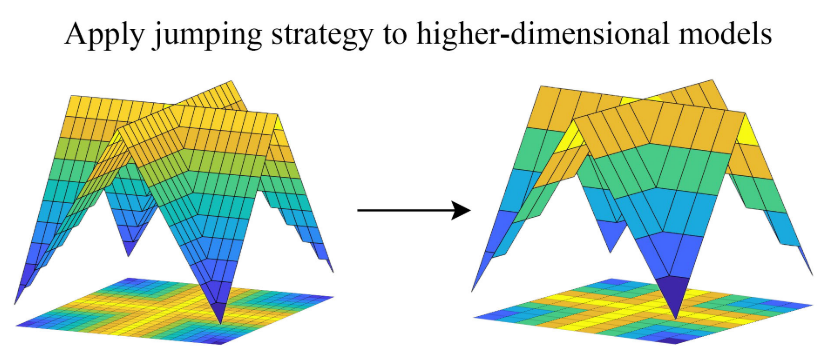
在探索阶段借鉴了图像裁剪与重组技术的跳跃策略,旨在增强搜索位置的分布广度。将图像划分为 36x36 的小块,然后按照特定规则重新排列,以保持整体形状。这种技术利用人眼在观察图像时,通过整体和局部特征的组合来感知图像,从而对局部信息的丢失相对不敏感。将这一概念扩展到高维数据,该方法在保持元数据的关键特征的同时,将搜索分布在多个区域,以提高搜索效率。
f j u m p = ( l b ( 1 ) − u b ( 1 ) ) δ , δ ∈ [ 100 , 2000 ] (4) f_{jump}=\frac{(lb(1)-ub(1))}{\delta},\delta\in[100,2000]\tag{4} fjump=δ(lb(1)−ub(1)),δ∈[100,2000](4)
人类发展阶段
在人类发展的各个阶段,HEOA将人类社会分为四种不同的角色:领导者、探索者、追随者和失败者。每个角色采用独特的搜索策略,共同协作探索全局最优解。
领导者拥有丰富的知识,通常位于最优区域。在进行的实验中,预适应前40%的个体被指定为领导者。他们利用现有的知识,开始探索人类发展的优越领域:
X i t + 1 = { ω ⋅ X i t ⋅ exp ( − t r a n d ⋅ M a x i t e r ) , R < A ω ⋅ X i t + R n ⋅ o n e s ( 1 , d i m ) , R ≥ A (5) X_i^{t+1}=\begin{cases}\omega\cdot X_i^t\cdot\exp(\frac{-t}{rand\cdot Max_{iter}}),R<A\\\\\omega\cdot X_i^t+Rn\cdot ones(1,dim),R\geq A\end{cases}\tag{5} Xit+1=⎩ ⎨ ⎧ω⋅Xit⋅exp(rand⋅Maxiter−t),R<Aω⋅Xit+Rn⋅ones(1,dim),R≥A(5)
知识获取的容易度系数w,随着发展的推进逐渐减小:
ω = 0.2 cos ( π 2 ( 1 − t M a x i t e r ) ) (6) \omega=0.2\cos(\frac\pi2(1-\frac t{Max_{iter}}))\tag{6} ω=0.2cos(2π(1−Maxitert))(6)
探索者在探索未知领域以发现全局最佳解决方案方面发挥着至关重要的作用。在进行的实验中,在种群中健康度排名前40%到80%的个体被指定为探索者:
X i t + 1 = R n ⋅ exp ( X w o r s t t 2 − X i t 2 i 2 ) (7) X_i^{t+1}=Rn\cdot\exp(\frac{X_{worst}^t{}^2-X_i^{t2}}{i^2})\tag{7} Xit+1=Rn⋅exp(i2Xworstt2−Xit2)(7)
跟随者坚持最具适应性的领导者的指导,跟随他们的脚步。在进行的实验中,最上层的80%至90%的人口被分配为追随者的角色:
X i t + 1 = X i t + 2 ω ⋅ R d ⋅ ( X b e s t t − X i t ) (8) X_i^{t+1}=X_i^t+2\omega\cdot Rd\cdot\left(X_{best}^t-X_i^t\right)\tag{8} Xit+1=Xit+2ω⋅Rd⋅(Xbestt−Xit)(8)
失败者是指不能很好地适应环境而留在人群中的个体。这些不适应社会的失败者将被淘汰,在适合人类发展的地区通过繁殖来补充人口:
X i t + 1 = X b e s t + ( X b e s t − X i t ) ⋅ R n (9) X_i^{t+1}=X_{best}+\left(X_{best}-X_i^t\right)\cdotp Rn\tag{9} Xit+1=Xbest+(Xbest−Xit)⋅Rn(9)
伪代码

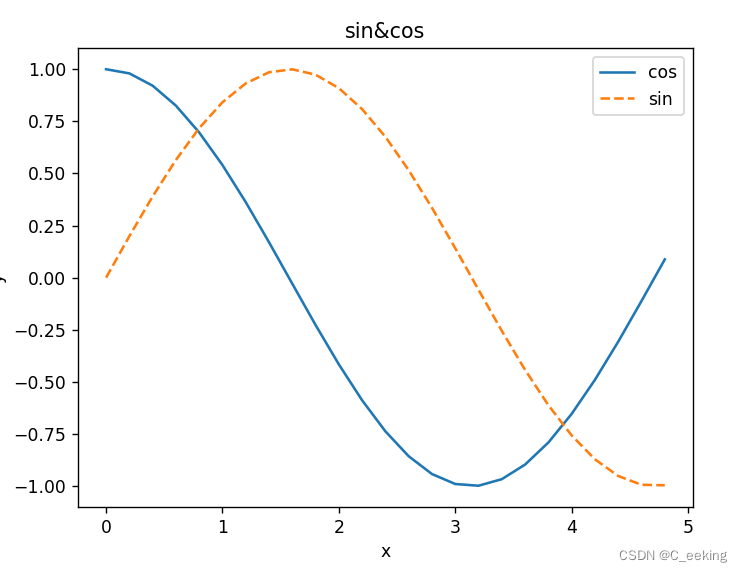
3.结果展示
使用测试框架,测试HEOA性能 一键run.m
- 【智能算法】省时方便,智能算法统计指标——一键运行~
CEC2017-F22
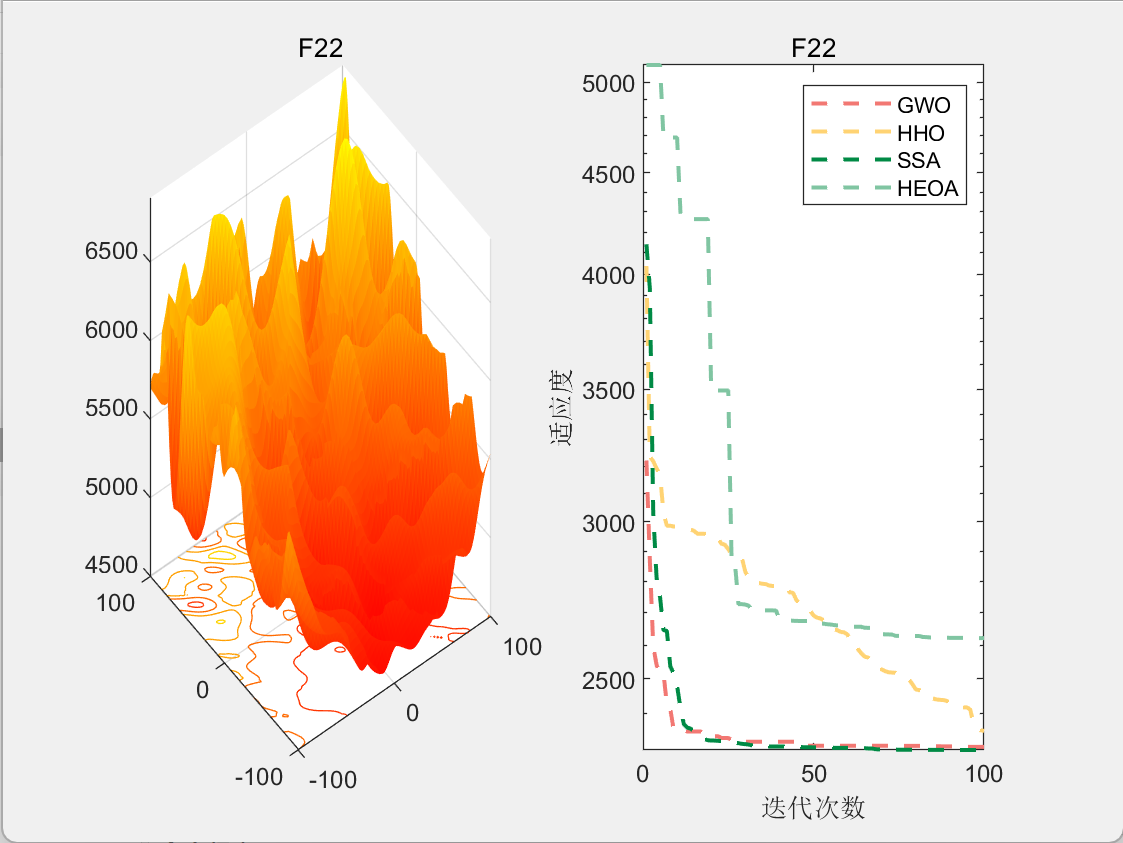
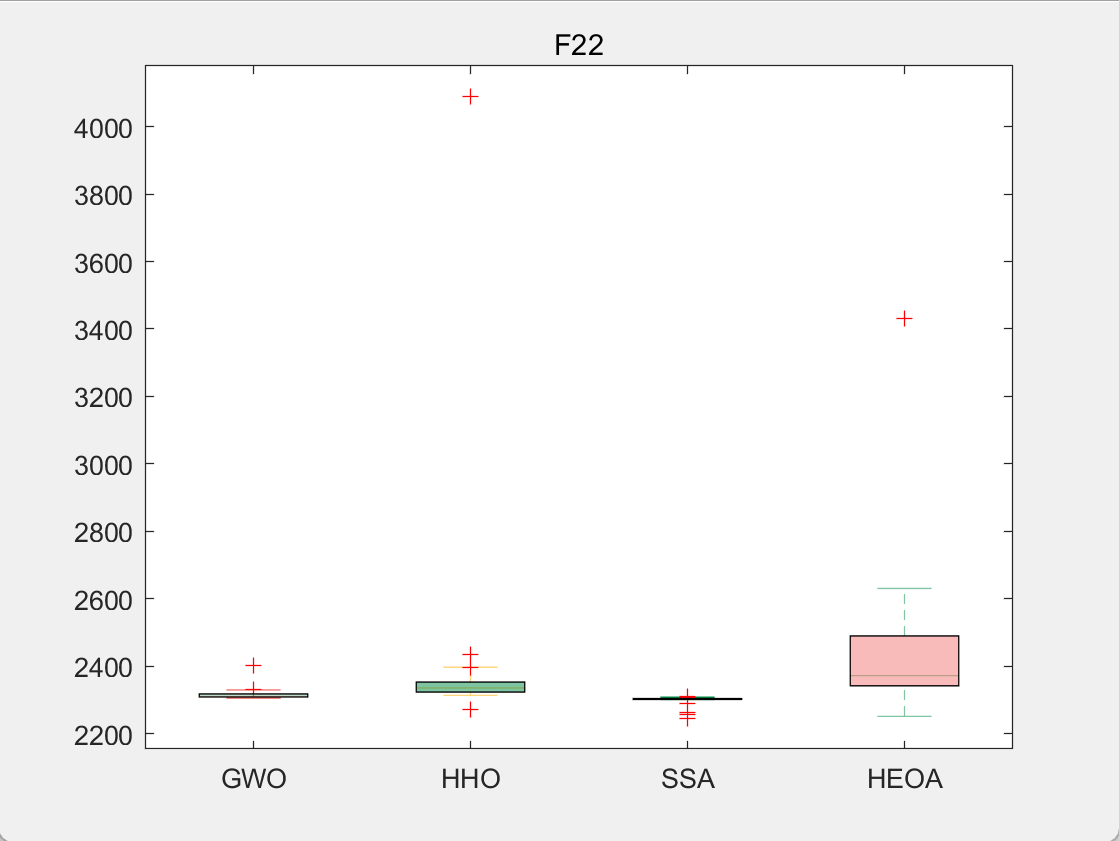

4.参考文献
[1] Lian J, Hui G. Human evolutionary optimization algorithm[J]. Expert Systems with Applications, 2024, 241: 122638.