车间调度系列文章:
- 1、路径优化历史文章
- 2、路径优化丨带时间窗和载重约束的CVRPTW问题-改进遗传算法:算例RC108
- 3、路径优化丨带时间窗和载重约束的CVRPTW问题-改进和声搜索算法:算例RC108
- 4、路径优化丨复现论文-网约拼车出行的乘客车辆匹配及路径优化
- 5、多车场路径优化丨遗传算法求解MDCVRP问题
- 6、论文复现详解丨多车场路径优化问题:粒子群+模拟退火算法求解
- 7、路径优化丨复现论文外卖路径优化GA求解VRPTW
- 8、多车场路径优化丨蚁群算法求解MDCVRP问题
- 9、路径优化丨复现论文多车场带货物权重车辆路径问题:改进邻域搜索算法
- 10、多车场多车型路径问题求解复现丨改进猫群算法求解
问题描述
多车场多车型车辆路径问题可描述为:多个车场内配备多种类型的车辆,服务周边的客户,已知所有客户的需求,同时,已知客户的位置坐标,通过合理地分配车辆和客户,制定合理的配送方案,使得配送成本最低。示意图如下:
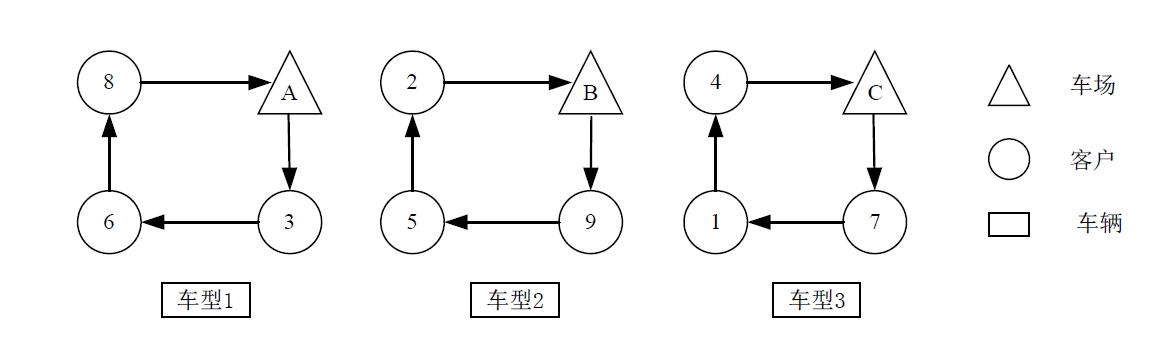
为了方便对问题进行分析和求解,首先设置了如下假设:
- (1)车辆完成任务后,停靠原车场;
- (2)每个车场拥有不同类型的车辆,不同类型车辆的载重、使用成本等属性可能不同;
- (3)一辆车最多被使用一次;
- (4)已知客户相关信息,各个车场和车辆的相关信息已知;
- (5)每辆车至少可以服务一个客户,即每辆车的额定载重不小于任意一个客户的需求;
- (6)每个客户只能被一辆车服务,且只访问一次。
数学模型
具体模型见参考文献。模型相关的参数和变量如下:
𝑀:客户的数量;
𝐾:车辆的数量;
𝑁:车场的数量;
𝐿 :车型的数量;
𝑦𝑛:车场𝑛(𝑛 = 1,2,3 … , 𝑁)内的车辆数目;
𝑅𝑛𝑙:车场𝑛(𝑛 = 1,2,3 … , 𝑁)的第𝑙 (𝑙 = 1,2,3 … , 𝐿)种类型的车辆数目;
𝐼𝑘:车辆 𝑘 服务客户的编号集合;
𝑓𝑘1:车辆𝑘 的固定成本;
𝑓𝑘2:车辆𝑘 的可变成本;
𝑄1𝑘:车辆𝑘 的额定载重;
𝑄2𝑙:车型𝑙 的额定载重;
𝑑𝑖𝑗:节点𝑖 到节点𝑗 的距离;
𝑞𝑖:节点𝑖 的需求量;


简单说目标函数是目标函数是不变成本和可变成本之和。不变成本是每辆车的固定成本,可变成本是每辆车的运行成本,和经过的客户点有关系。

数据预处理
论文数据,
30个客户:
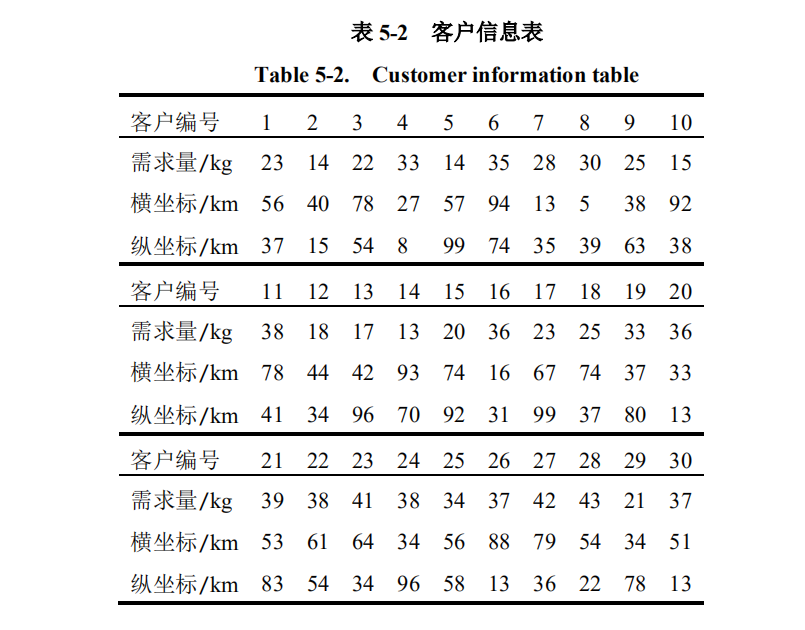
10个车辆:
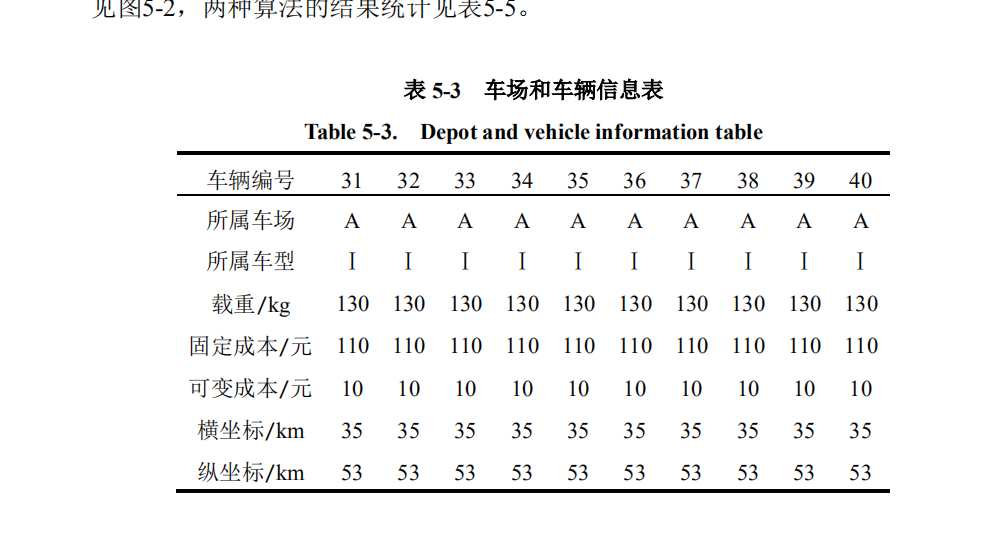
复制数据到对应txt:
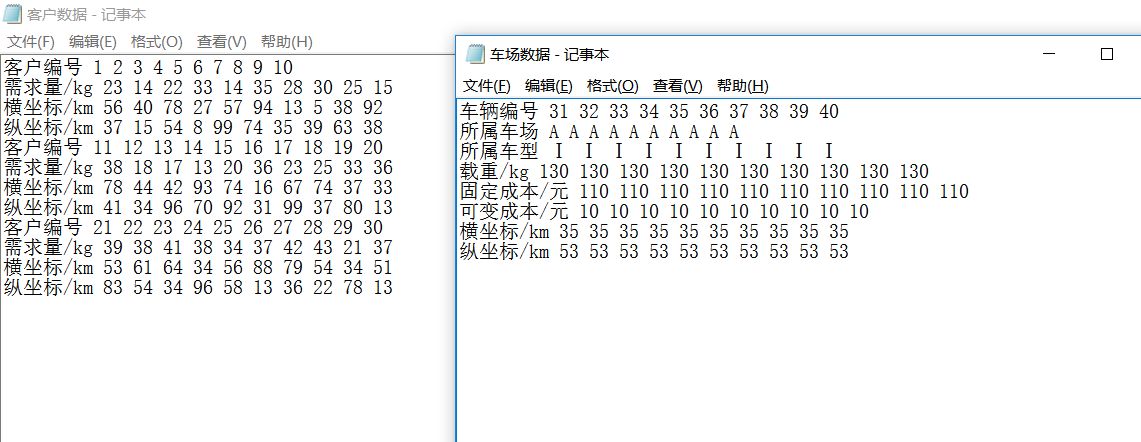
正则读取对应行就行。
import redef get_customer():with open('客户数据.txt', 'r') as file:content = file.read() # 读取文件内容demand_inf = re.findall(r'需求量/kg[0-9 ]+', content)xust_inf = re.findall(r'横坐标/km[0-9 ]+', content)yust_inf = re.findall(r'纵坐标/km[0-9 ]+', content)demand, x, y = [], [], []for dxy in range(len(demand_inf)):demand += [int(d) for d in re.findall(r'[0-9]+', demand_inf[dxy])]x += [int(xx) for xx in re.findall(r'[0-9]+', xust_inf[dxy])]y += [int(yy) for yy in re.findall(r'[0-9]+', yust_inf[dxy])]return demand, x, ydef get_park():with open('车场数据.txt', 'r') as file:content = file.read() # 读取文件内容load_inf = re.findall(r'载重/kg[0-9 ]+', content)unchange_inf = re.findall(r'固定成本/元[0-9 ]+', content)change_inf = re.findall(r'可变成本/元[0-9 ]+', content)xust_inf = re.findall(r'横坐标/km[0-9 ]+', content)yust_inf = re.findall(r'纵坐标/km[0-9 ]+', content)load_all = [int(l) for l in re.findall(r'[0-9]+', load_inf[0])]unchange_c = [int(u) for u in re.findall(r'[0-9]+', unchange_inf[0])]change_c = [int(c) for c in re.findall(r'[0-9]+', change_inf[0])]x_center = [int(xx) for xx in re.findall(r'[0-9]+', xust_inf[0])]y_center = [int(yy) for yy in re.findall(r'[0-9]+', yust_inf[0])]return load_all, unchange_c, change_c, x_center, y_center运行环境
windows系统,python3.6.0,第三方库及版本号如下:
numpy==1.18.5
matplotlib==3.2.1
第三方库需要在安装完python之后,额外安装,以前文章有讲述过安装第三方库的解决办法。
算法设计
1、编码
编码介绍
论文采用实数编码,一段表示车辆,一段表示客户:

本文做了改进:把编码拆开成2段,分别是车辆和客户,为了下面的猫群算子操作更容易。
编码生成
车辆编码生成: 随机打乱车辆编号
客户编码生成:随机选择一辆车的车场作为原点,扫码周围客户点,按距离形成序列,按载重依次分配给车辆。

代码:
def init_road(self):road_car = [[] for i in range(len(self.load_all))]car_idx = np.arange(len(self.load_all))random.shuffle(car_idx) # 随机打乱车辆编号idx = random.choice(car_idx) # 选择一个作为原点origin_x, origin_y = self.x_center[idx], self.y_center[idx]dist = [np.sqrt((self.x[point] - origin_x)**2 + (self.y[point] - origin_y)**2) for point in range(len(self.demand))]dist_sort = np.array(dist).argsort() # 计算与周围客户点距离后,按大小索引形成序列road = dist_sort.tolist()car_count = 0for cust_idx in dist_sort: # 遍历序列的每一个点idx1 = car_idx[car_count]if sum(np.array(self.demand)[road_car[idx1]]) + self.demand[cust_idx] > self.load_all[idx1]:car_count += 1 # 载重不满足时换下一辆车idx1 = car_idx[car_count]road_car[idx1].append(cust_idx)return car_idx.tolist(), road_car, road
文献数据形成的可行编码如下:
车辆编码:[4, 9, 3, 7, 2, 0, 1, 6, 5, 8]
表示优先安排车辆5(4+1),车辆10配送,后面以此类推
客户编码:[8, 11, 24, 28, 21, 0, 18, 6, 15, 7, 22, 20, 27, 1, 19, 17, 2, 23, 29, 12, 10, 3, 26, 4, 14, 16, 9, 13, 5, 25]
表示优先服务客户9(8+1),客户12,后面以此类推
车辆客户编码:[[29, 12, 10, 3], [26, 4, 14, 16, 9, 13], [19, 17, 2, 23], [15, 7, 22], [8, 11, 24, 28], [], [5, 25], [20, 27, 1], [], [21, 0, 18, 6]]
因为优先安排车辆5且考虑载重,所以8,11,24,28被分到第5个括号,然后21,0,18,6被分到最后一个括号,后面以此类推。其中,车辆6和车辆9没有分到,为空括号。
2、解码
一个车辆的解码如下:
-
1、 根据车辆和客户编码读出各点的坐标和需求;
-
2、 编码客户的第一个点时,计算车场到点的距离,其余点计算与上一个客户点的距离,更新可变成本;
-
3、每辆车遍历到最后一个点时,计算点到车场的距离,成本更新(包含不变成本),解码结束:
代码如下:
def decode(self, car_idx, road_car):fk1, fk2 = 1, 1C1 = 0C2 = [0 for i in range(len(self.load_all))]count = 0for rc in road_car:fk1 = self.unchange_c[count] # 单位固定成本fk2 = self.change_c[count] # 单位可变成本if rc: # 车辆的客户点非空C1 += fk1 # 固定成本计算idx = car_idx[count]for point in rc:if C2[count] == 0: # 车场到第一个客户origin_x, origin_y = self.x_center[idx], self.y_center[idx]dist = np.sqrt((self.x[point] - origin_x)**2 + (self.y[point] - origin_y)**2) C2[count] += dist*fk2 # 可变成本计算 else : # 客户点之间运行dist = np.sqrt((self.x[point] - x_start)**2 + (self.y[point] - y_start)**2) C2[count] += dist*fk2 # 可变成本计算x_start, y_start = self.x[point], self.y[point] # 车辆再回车场dist = np.sqrt((origin_x - x_start)**2 + (origin_y - y_start)**2) C2[count] += dist*fk2 # 可变成本计算count += 1return C1, C2, C1 + sum(C2)
猫群算子
逆序邻域搜索算子

车辆或者客户截取一段编码逆序即可:
def Reverse_order(road, signal):loc = random.sample(range(len(road)), 2) # 选取2个位置loc.sort() # 保证位置从小到大road1, road2, road3 = road[:loc[0]], road[loc[0]:loc[1]], road[loc[1]:] # 截取编码road2.reverse() # 逆序return road1 + road2 + road3 # 返回合并的新代码
1—opt算子
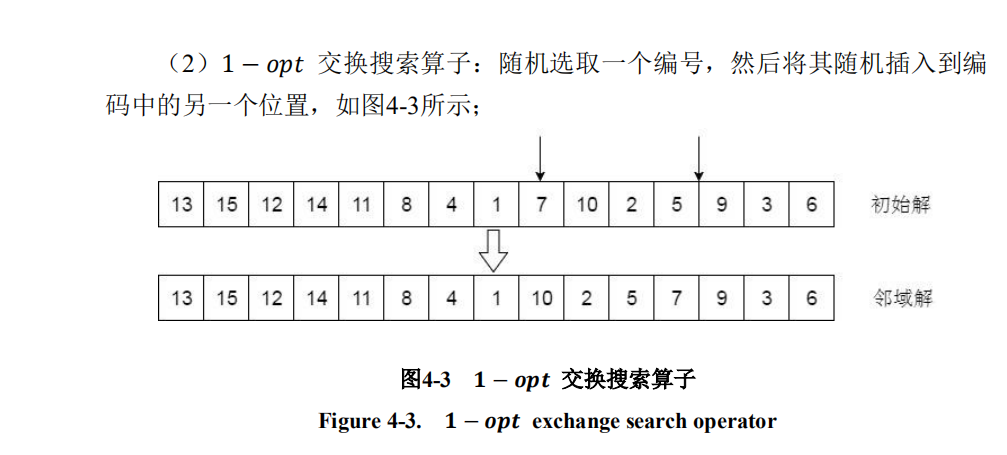
代码:
def opt_1(road, signal):loc = random.sample(range(len(road)), 2) # 选取2个位置if signal==1:while max(loc) < len(road)/2: # 保证车辆编码的一个位置在后半边编码,文献有说到loc = random.sample(range(len(road)), 2)loc.sort() # 位置升序a = road[loc[0]]b_idx = loc[1]road.remove(a) # 找到编码,移除road.insert(b_idx-1, a) # 插入编码,-1是因为上一步移除,位置缩进return road
2-opt算子
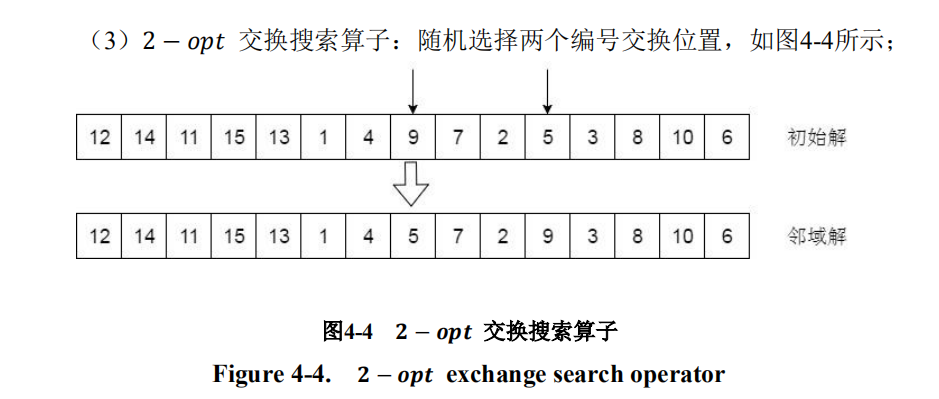
代码:
def opt_2(road, signal):loc = random.sample(range(len(road)), 2) if signal==1:while max(loc) < len(road)/2: # 保证车辆编码的一个位置在后半边编码,文献有说到loc = random.sample(range(len(road)), 2)road[loc[0]], road[loc[1]] = road[loc[1]], road[loc[0]] # 2个位置交换return road
3—opt算子
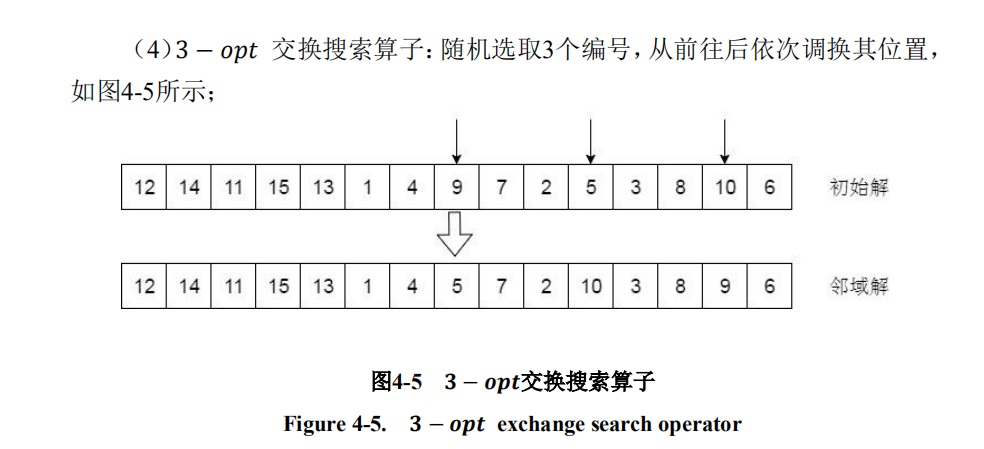
相当于上面的2_opt交换2次
代码:
def opt_3(road, signal):loc = random.sample(range(len(road)), 3)if signal==1:while max(loc) < len(road)/2: # 保证车辆编码的一个位置在后半边编码,文献有说到loc = random.sample(range(len(road)), 3)road[loc[0]], road[loc[1]] = road[loc[1]], road[loc[0]] # 交换1次road[loc[1]], road[loc[2]] = road[loc[2]], road[loc[1]] # 交换2次return road
2、跟踪最优算子

简单来说:2段编码截取长度为U的一段,找出相同的基因,编码2去掉这段基因,剩余的基因左连接去掉的这段基因。详细介绍见文献
def follow_best(road1, road2, U):road2 = road2.tolist()a_u = road1[:U] # 截取1段b_u = road2[:U] # 截取1段road3 = []for a in a_u: if a in b_u: # 截取片段有相同基因时road3.append(a) # 保存基因road2.remove(a) # 编码2移除基因road3 += road2 # 最后左连接return road3
3、跟踪中心算子
重要的是找出中心编码,找到中心编码后的该编码看作最优编码,跟踪方式相同。中心编码寻找如下:
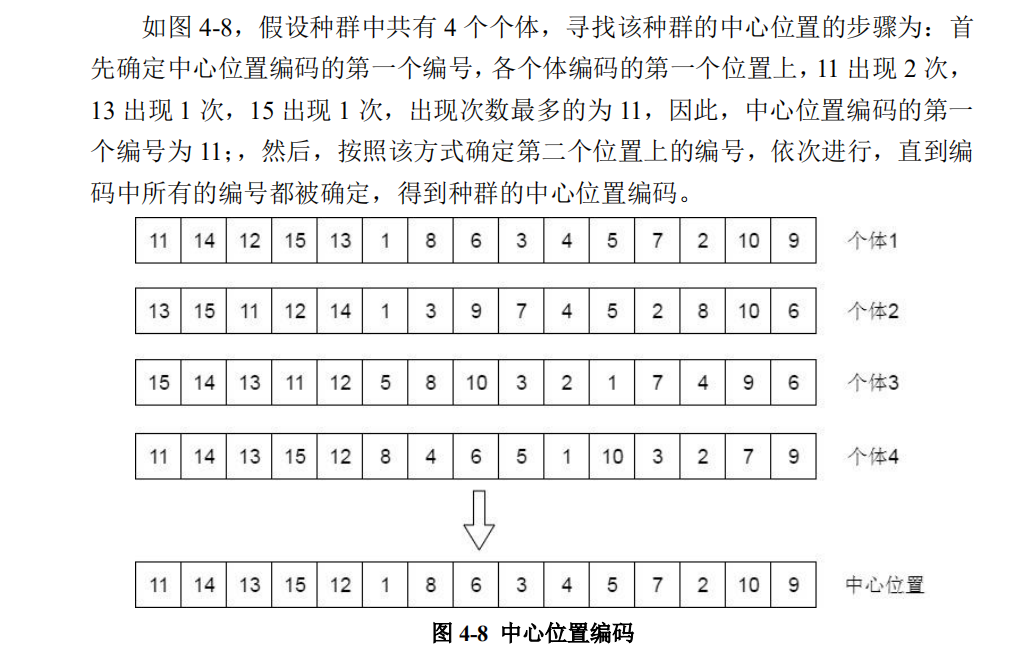
简单来说,统计所有位置出现最多的基因,保证客户基因不重复的情况,出现次数最多基因连起来的就是中心编码
代码:
def center_road(T_road):cent_road = []T_road = T_road.tolist() # 备份一份while T_road[0]: # 当还存在编码非空时road_time = [ro[0] for ro in T_road] # 各个编码的第一个基因b = Counter(road_time) # 计数ansdict = b.most_common(1) # 出现次数最多的情况rox = ansdict[0][0]cent_road.append(rox) # 出现最多的基因for i in range(len(T_road)): # 中心编码找到一个基因后,所有编码依次移除该基因T_road[i].remove(rox)return cent_road
改进猫群算法设计
改进猫群算法的具体步骤如下:
-
(1)初始化参数和路径信息,并且生成初始的种群;
-
(2)根据设置的分组率,选出实施搜寻行为的个体,剩余的个体则全部实施跟踪行为;
-
(3)个体根据各自的行为,分别更新位置,即跟踪模式下的个体执行跟踪模式,其余则执行搜寻模式;
-
(4)更新种群中个体的适应度,同时记录最优个体;
-
(5)判断迭代次数,若代数符合算法的设置,则对当前最优解进行一次模拟退火搜索;否则,则跳过该步骤,转步骤(6);
-
(6)检查结束条件。若符合算法终止条件,则得到优化结果;否则,继续执行(2)
推文没设置分组率,全部都进行搜寻和跟踪,有兴趣自行设置,修改比较容易,文献是最后一次迭代对最优个体进行一次模拟退火,
1、搜寻模式
(1)将 𝐿𝑠 复制 𝑉 份,并存入记忆池;
(2)对每个副本实施搜索,首先确定对位置编码的车辆编码部分或客户编码部分进行搜索。若𝑣(𝑣 = 1,2,3, … … , 𝑉)能够被 4 整除(即每 4 个中有一个对车辆编码搜索),则对车辆编码部分进行搜索;否则,对客户编码部分进行搜索。搜索完成之后,获得新的候选位置 𝐿𝑠𝑣 (𝑣 = 1,2,3, … … , 𝑉);
(3)解码计算每个候选位置 𝐿𝑠𝑣 的适应度 𝑓𝑠𝑣 ,记录其中最优的适应度为 𝑓b ,最优位置为 𝐿b ;
(4)若 𝑓𝑠 ≥ 𝑓b ,则保持𝐿𝑠 不变;否则,用𝐿b 代替 𝐿𝑠 。
简单来说:个体在执行搜寻模式时,使用选择算子从记忆池中选择适应度最高(成本最低)的位置作为该个体的新位置。
代码:
def search(self, car_idx, road): # 搜索模式road_car = self.cd.road_code(car_idx, road) # 客户路径转换C1, C2, fs = self.cd.decode(car_idx, road_car) # 初始的成本T_road = np.zeros((self.𝑉, len(road)), dtype = np.int) # 客户池T_caridx = np.zeros((self.𝑉, len(car_idx)), dtype = np.int) # 车辆池T_road[:] = roadT_caridx[:] = car_idx for v_idx in range(self.𝑉):Operator = ['Reverse_order', 'opt_1', 'opt_2', 'opt_3']oper = random.choice(Operator) # 随机选择一个算子car_code = T_caridx[v_idx].tolist()ro_code = T_road[v_idx].tolist()if v_idx%4 == 0: # 如果被4整除,车辆搜索 car_code = eval(f'cat.{oper}(car_code, 1)')else: # 否则,客户搜索ro_code = eval(f'cat.{oper}(ro_code, 0)')road_car = self.cd.road_code(car_code, ro_code) # 路径转换C1, C2, fb = self.cd.decode(car_code, road_car) # 新路径的成本if fb < fs: # 如果成本优于初始成本,更新编码和成本car_idx = car_coderoad = ro_codefs = fbreturn car_idx, road, fs
2、跟踪模式
改进猫群算法的跟踪模式有两种情况:
- 1、跟踪种群中的最优个体的位置,
- 2、跟踪种群的中心位置。
需要说明的是,执行跟踪模式的猫,每次只能选择执行跟踪其中的一个位置,即每次随机选择跟踪最优个体或中心位置。
每次跟踪在一定概率下跟踪最优个体,否则跟踪中心个体,相关算子上面有介绍。
代码:
def follow(self, T_car, T_road): # 跟踪模式f_all = [self.cd.decode(T_car[i],self.cd.road_code(T_car[i],T_road[i]))[-1] for i in range(len(T_car))]best_idx = f_all.index(min(f_all)) f_best = min(f_all) best_car, best_road = T_car[best_idx].tolist().copy(), T_road[best_idx].tolist().copy()# 最优个体center_road = cat.center_road(T_road) # 中心个体center_car = cat.center_road(T_car)for i in range(len(f_all)):car = T_car[i]road = T_road[i]if random.random() < self.𝜃 and i != best_idx: # 一定概率下跟踪最优个体road_new = cat.follow_best(best_road, road, self.𝑈)road_car = self.cd.road_code(car, road_new)C1, C2, fb = self.cd.decode(car, road_car)if fb < f_best: # 如果新个体优于最优个体best_car = carbest_road = road_new # 更新最优客户路径f_best = fbelse: # 否则跟踪中心个体road_new = cat.follow_best(center_road, road, self.𝑈)road_car = self.cd.road_code(car, road_new)C1, C2, fb = self.cd.decode(car, road_car)if fb < f_best:best_car = carbest_road = road_newf_best = fbT_road[i] = road_new # 更新种群客户road_car = self.cd.road_code(best_car, best_road)C1, C2, fs = self.cd.decode(best_car, road_car) return T_road, best_car, best_road, f_best
3、模拟退火算法
概念不再赘述,文献的算法步骤是:
(1)在前𝐻/2 次,对编码的客户编码部分实施变异,车辆编码部分不变,具体操作为:随机选择其中的一个算子,对客户编码部分执行搜索,产生新的位置,如果min(1, exp[−(𝑍(𝐿𝑏) − 𝑍(𝐿𝑎)) / 𝐸tem-])+ ≥ random(0,1),则令𝐿𝑎 = 𝐿𝑏;记录该过程的最优位置𝐹sa及其适应度𝑓sa;
(2)在后𝐻/2 次,对编码的车辆编码部分实施变异,客户编码部分不变,具体操作为;随机选择其中的一个算子,对车辆编码部分执行搜索,产生新的位置,如果min(1, exp[−(𝑍(𝐿𝑏) − 𝑍(𝐿𝑎)) / 𝐸tem-])+ ≥ random(0,1),则令𝐿𝑎 = 𝐿𝑏;记录该过程的最优位置𝐹sa及其适应度𝑓sa;
(3)令 𝐸tem = 𝐸tem ∗ 𝑟 ,若 𝐸tem ≤ 𝐸2,则终止搜索,进行判断:若𝑓sa > 𝑓best,则令𝐿best = 𝐿sa,𝑓best = 𝑓sa,否则,令𝐹best不变,避免出现退化;若 𝐸tem > 𝐸2,则重新回到步骤(1)。
简单来说,一定概率下接受新个体,且一直保留或更新最优个体。文献是再最后一次迭代后对最优个体进行模拟退火。
def Simul(self, best_car, best_road, f_best):if type(best_car) == np.ndarray:carx = best_car.tolist().copy()else:carx = best_car.copy()if type(best_road) == np.ndarray:roadx = best_road.tolist().copy()else:roadx = best_road.copy()fbx = f_bestroad_car = self.cd.road_code(best_car, best_road)C1, C2, fs = self.cd.decode(best_car, road_car) while self.𝐸1 > self.𝐸2:for i in range(self.𝐻):Operator = ['Reverse_order', 'opt_1', 'opt_2', 'opt_3']oper = random.choice(Operator)if i < self.𝐻/2:road1 = eval(f'cat.{oper}(roadx, 0)') # 产生新客户路径road_car = self.cd.road_code(carx, road1)C1, C2, fb = self.cd.decode(carx, road_car)if min(1, np.exp(-(fb-fbx)/self.𝐸1)) >= random.random(): # 一定概率接受新路径roadx = road1fbx = fbif fb < f_best: best_car = carx best_road = road1f_best = fbelse:car1 = eval(f'cat.{oper}(carx, 1)') # 产生新车辆路径road_car = self.cd.road_code(car1, roadx)C1, C2, fb = self.cd.decode(car1, road_car)if min(1, np.exp(-(fb-fbx)/self.𝐸1)) >= random.random():carx = car1fbx = fbif fb < f_best: # 成本得到优化就更新print('2222')best_car = car1best_road = roadxf_best = fbself.𝐸1 *= self.𝑟 # 温度更新return best_car, best_road, f_best
结果
设计主函数如下:
import data
from code_decode import co_de
import numpy as np
import paint
from cat_change import cat_chdemand, x, y = data.get_customer() # 客户数据
load_all, unchange_c, change_c, x_center, y_center = data.get_park() # 车辆数据
parm_data = [demand, x, y, load_all, unchange_c, change_c, x_center, y_center]
cd = co_de(parm_data) # 解码模块
car_init, road_car, road_init = cd.init_road()
C1, C2, fs = cd.decode(car_init, road_car) # 初始成本𝑆 = 20 # 猫的种群数量
δ = 0.1 # 分组率
𝑉 = 40 # 记忆池容量
𝑇 = 10 # 迭代总次数
𝑈 = 18 # 比对长度
𝜃 = 1 # 跟踪最优个体概率
𝜃1 = 0.2 # 跟踪中心位置概率1 − 𝜃
𝐸1 = 100 # 初始温度
𝐸2 = 95 # 终止温度
𝑟 = 0.99 # 降温系数
𝐻 = 10 # 内循环迭代次数ch = cat_ch(𝑆, δ, 𝑉, 𝑇, 𝑈, 𝜃, 𝜃1, 𝐸1, 𝐸2, 𝑟, 𝐻, cd) # 改进猫群算法模块best_car, best_road, f_best, result = ch.total(car_init, road_init, fs) # 结果
road_car = cd.road_code(best_car, best_road) # 编码转换
C1, C2, fb = cd.decode(best_car, road_car)
print("\n成本验证:",fb)
print('车辆编码:', best_car)
print('客户编码:', best_road)
print('车辆路径编码:', road_car)
paint.draw(x, y, x_center, y_center, best_car, road_car, fb) # 路径图
paint.draw_change(result) # 成本变化图
运行结果
结果如下:
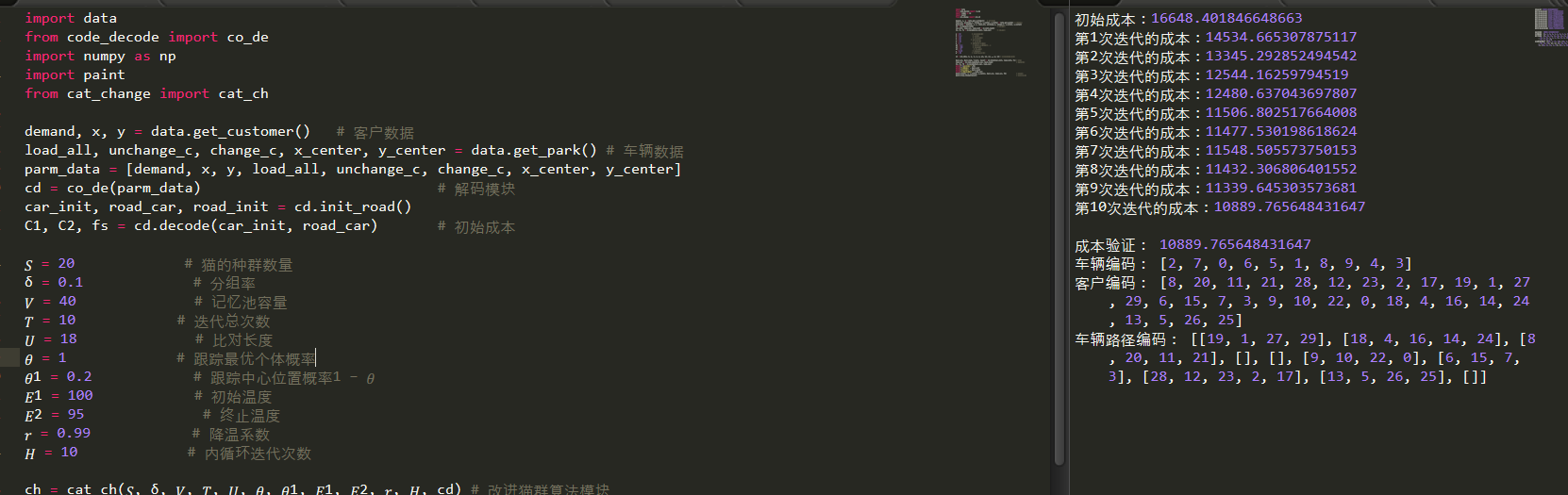
路径图:

成本随迭代次数的变化图如下:

还有优化空间,增大种群规模和迭代次数试试。
小结
-
本文主要是对参考论文进行复现,有小改动,但基本是复现原文,具体算法步骤见文献,不做过多介绍。本推文只是复现文献的部分内容,严格来说是单车场路径规划问题,应该文献的多车场数据也能运行,但还没做测试,不能运行修改也不会很大。至于带时间窗的模型,可能后续会复现。
-
本文数据和算法皆可修改(考虑运行时间,推文把一些运行参数调低)。
-
参考文献:
[1]蒋权威.多车场多车型车辆路径问题的改进猫群算法[D].浙江工业大学,2020.DOI:10.27463/d.cnki.gzgyu.2020.001279.
代码
为了方便和便于修改和测试,把代码在6个代码里。有兴趣可以任意合并,减少文件数。
演示视频:
论文复现丨多车型多车场路径优化问题:猫群算法求解
完整算法+数据:
完整算法源码+数据:见下方微信公众号:关注后回复:调度

# 微信公众号:学长带你飞
# 主要更新方向:1、柔性车间调度问题求解算法
# 2、学术写作技巧
# 3、读书感悟
# @Author : Jack Hao