矩阵相关运算1-编程知识

矩阵相关运算1

矩阵运算是线性代数中的一个核心部分，它包含了许多不同类型的操作，可以应用于各种科学和工程问题中。

矩阵加法和减法

矩阵加法和减法需要两个矩阵具有相同的维度。操作是逐元素进行的：

C=A+B or C=A−B

其中 A,B 和 C 是矩阵，且 Cij=Aij+Bij（或减法相应地）。
假设有两个矩阵 A 和 B：

A=[1   23   4]
B=[5   67   8]

加法运算 A+B的结果是：

A+B=[1+5   2+63+7  4+8]=[6      810    12]

矩阵乘法

矩阵乘法涉及两个矩阵，其中第一个矩阵的列数必须与第二个矩阵的行数相等。如果 A是一个 m×n 矩阵，B 是一个 n×p矩阵，则它们的乘积 C 将是一个 m×p 矩阵，其中：
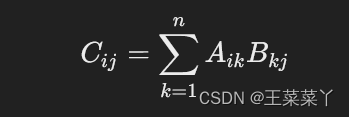在这里插入图片描述若 A 和 B 如下：

A=[1   23   4]
B=[2  0 1  2]

乘法运算 AB 的结果是：

AB=[1∗2+2∗1     1∗0+2∗2  3∗2+4∗1     3∗0+4∗2]=[4   410  8]

矩阵的逆

一个方阵的逆存在于当且仅当其行列式不为零时。如果 A 是一个 n×n 矩阵，那么它的逆 A⁻¹ 满足：
AA⁻¹=I
A⁻¹A=I
在这里插入图片描述

对于矩阵 A：

A=[1   23   4]

若存在，A 的逆 A⁻¹是：
在这里插入图片描述

转置

一个矩阵的转置是将其行与列互换得到的矩阵。如果 AA是一个 m×n 矩阵，则其转置 A^T 是一个 n×m矩阵。
在这里插入图片描述

行列式的值

在这里插入图片描述

代码（python）

import numpy as np# 创建矩阵 A 和 B
A = np.array([[1, 2], [3, 4]])
B = np.array([[2, 0], [1, 2]])# 矩阵加法
C = A + B# 矩阵乘法
D = np.dot(A, B)# 矩阵的逆
E = np.linalg.inv(A)# 矩阵的行列式
detA = np.linalg.det(A)# 矩阵的转置
F = A.Tprint("加法结果:", C)
print("乘法结果:", D)
print("逆矩阵:", E)
print("行列式:", detA)
print("转置矩阵:", F)