卷积层是卷积神经网络中的核心模块，**卷积层的目的是提取输入特征图的特征，**如下图所示，卷积核可以提取图像中的边缘信息。卷积也成为过滤器，即Filter
在这里插入图片描述

1 卷积的计算方法

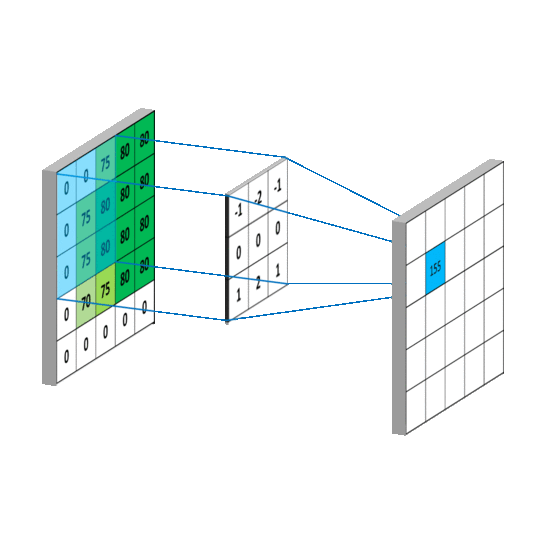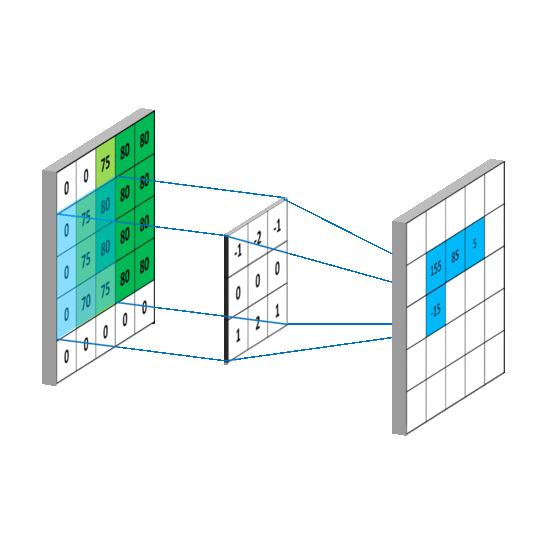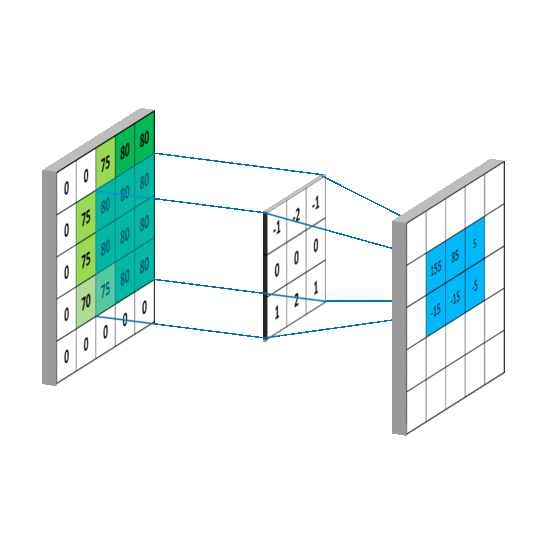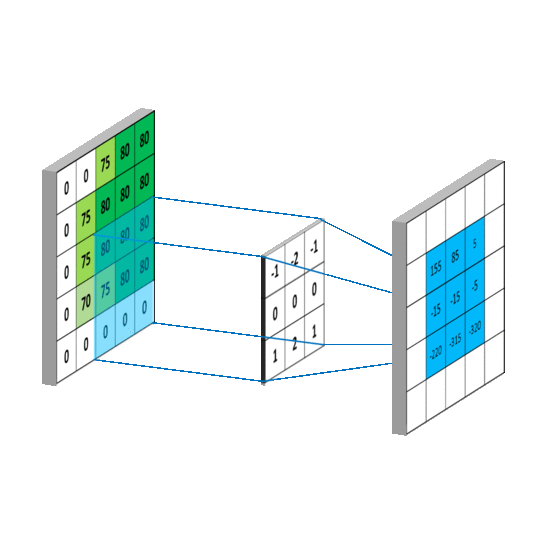
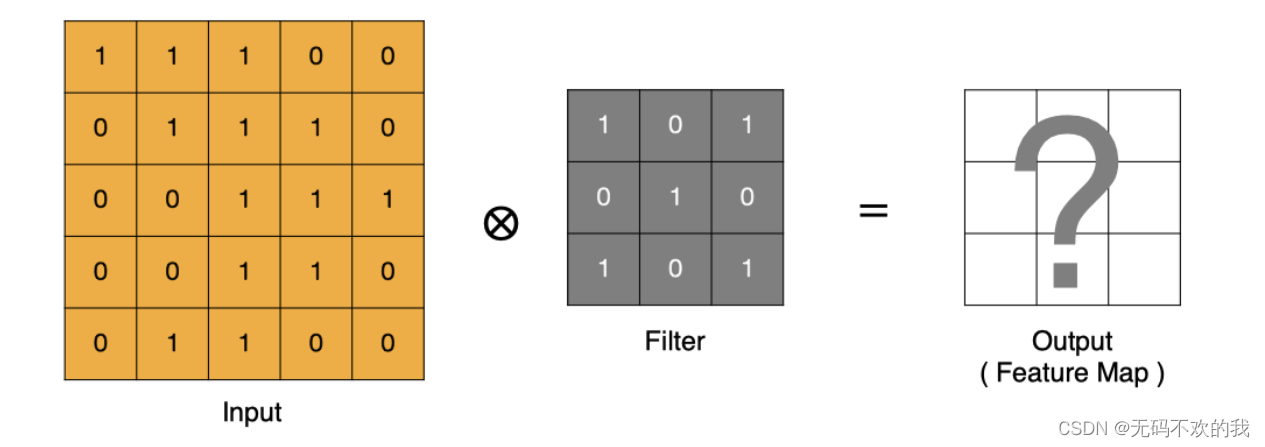
在这里插入图片描述

卷积运算本质上就是在滤波器和输入数据的局部区域间做点积

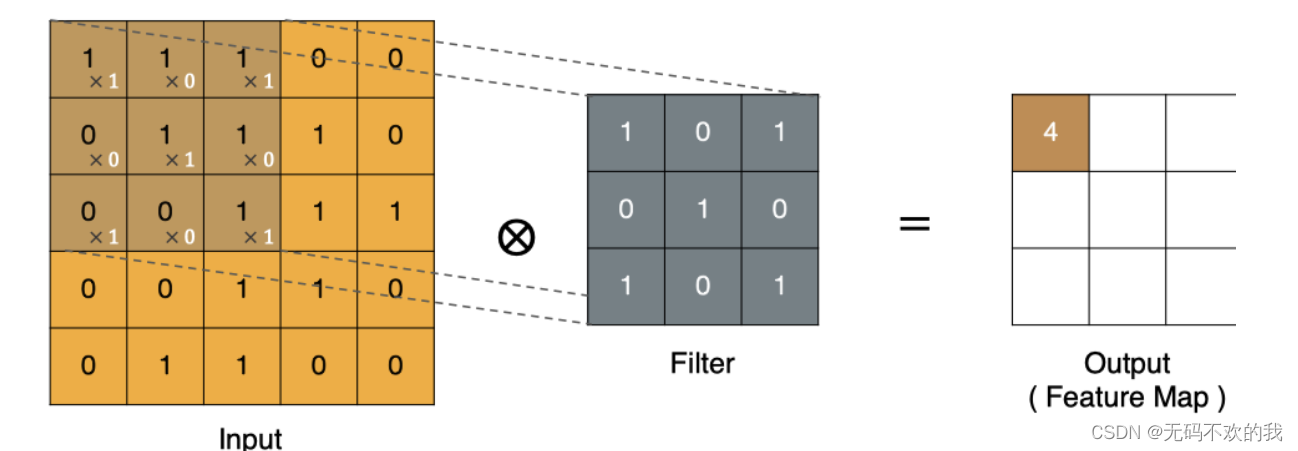
注意：

卷积核中的数字的来源跟前文中的权重w相同，刚开始初始化一个值（初始化方法跟权重的初始化方法相同），然后再通过不断的学习和反向传播进行更新。
卷积核/过滤器大小，一般会选择为奇数（因为尺寸为奇数的卷积核可以找到中心点），比如有1 * 1， 3 * 3， 5 * 5 ，一般选用尺寸较小的卷积核，比如3 * 3的核使用的最多，因为核越大所包含的参数就越多。

左上角的点计算方法：
在这里插入图片描述
同理可以计算其他各点，得到最终的卷积结果，

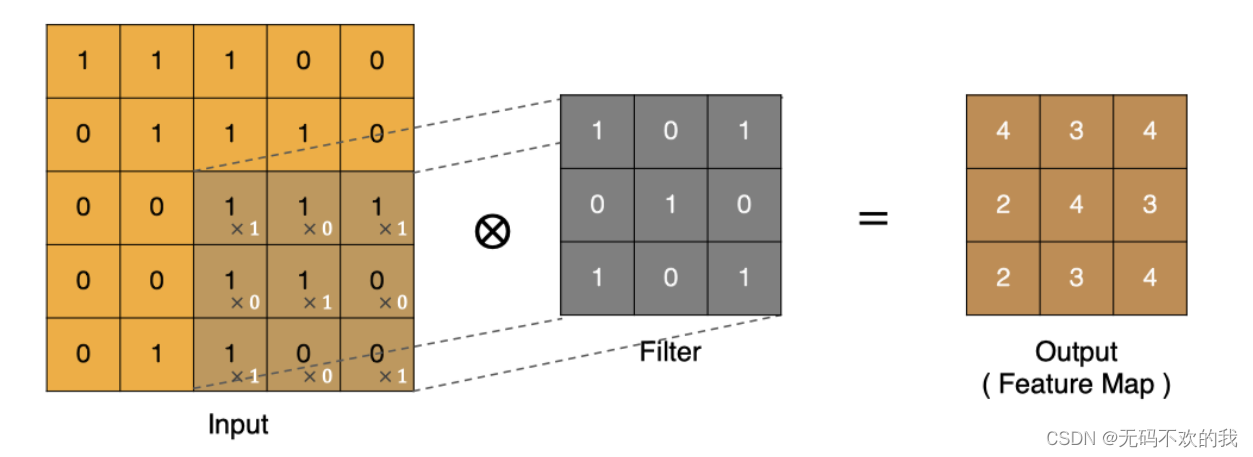
最后一点的计算方法是：

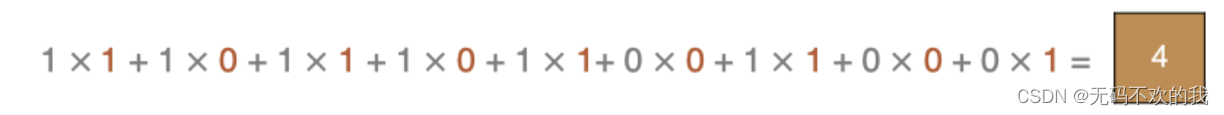
注意：因为每个卷积核都会带一个偏置，这里计算的时候默认为偏置值为0，如果偏置不为0，还需要加上偏置值

2 padding

在上述卷积过程中，特征图比原始图减小了很多，我们可以在原图像的周围进行padding,来保证在卷积过程中特征图大小不变。
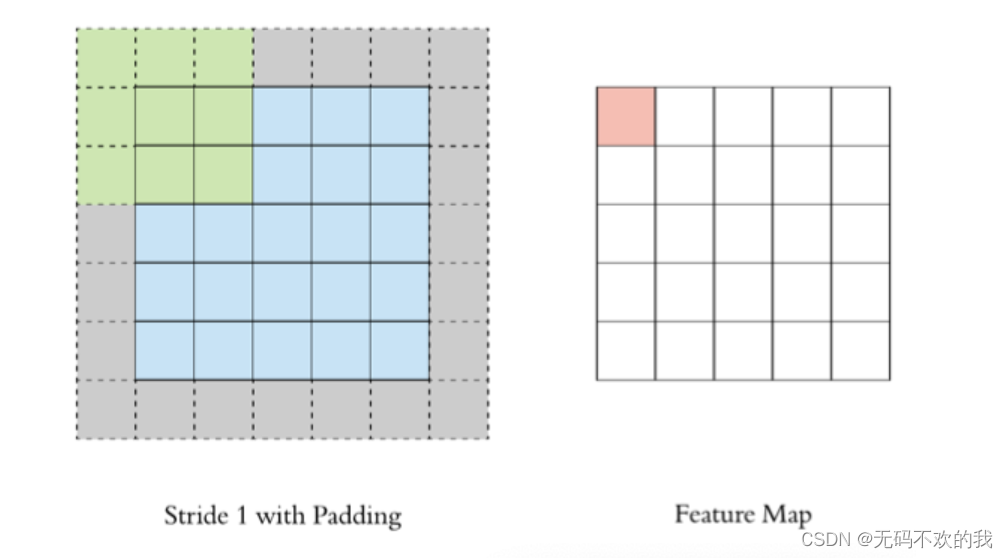
在这里插入图片描述

3 stride

按照步长为1来移动卷积核，计算特征图如下所示：
在这里插入图片描述
如果我们把stride增大,比如设为2，也是可以提取特征图的，如下图所示：

步长越大，特征图会变得越小

4 多通道卷积

实际中的图像都是多个通道组成的，我们怎么计算卷积呢？
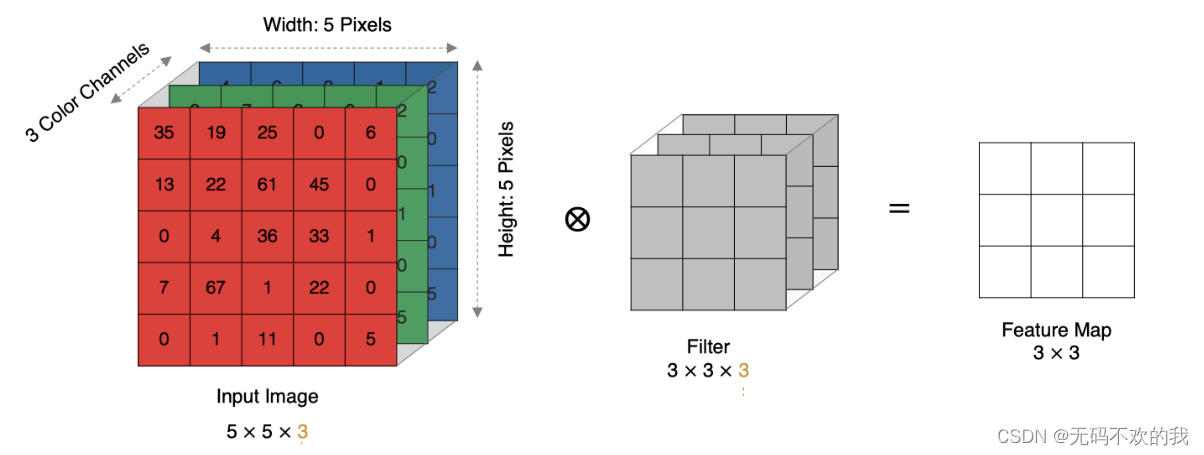
在这里插入图片描述
计算方法如下：当输入有多个通道（channel）时(例如图片可以有 RGB 三个通道)，卷积核需要拥有相同的通道数（channel）,每个卷积核 channel 与输入层的对应 channel 进行卷积，将每个 channel 的卷积结果按位相加得到最终的特征图（Feature Map）。注意，因为每个卷积核都会带一个偏置，这里计算的时候默认为偏置值为0，如果偏置不为0，还需要加上偏置值

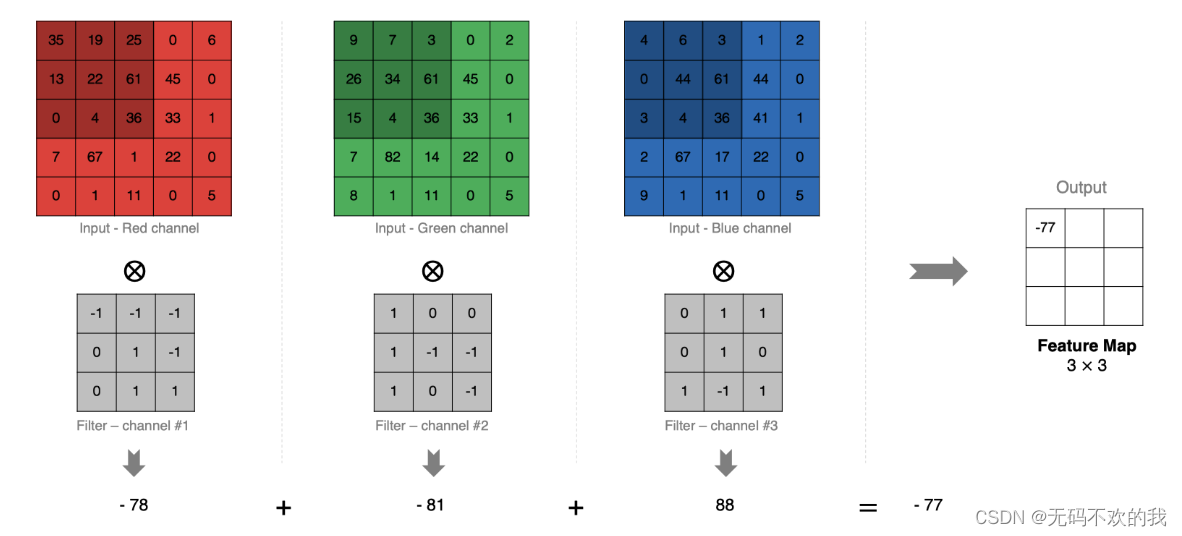
在这里插入图片描述

5 多卷积核卷积

如果有多个卷积核（ filter）时怎么计算呢？当有多个卷积核时，每个卷积核学习到不同的特征，对应产生包含多个特征图，也就是说最终产生的特征图有多个通道,（比如为了识别数字“八”，因为它由两个特征：一撇和一捺，那么就用两个卷积核分别来识别这两个特征）

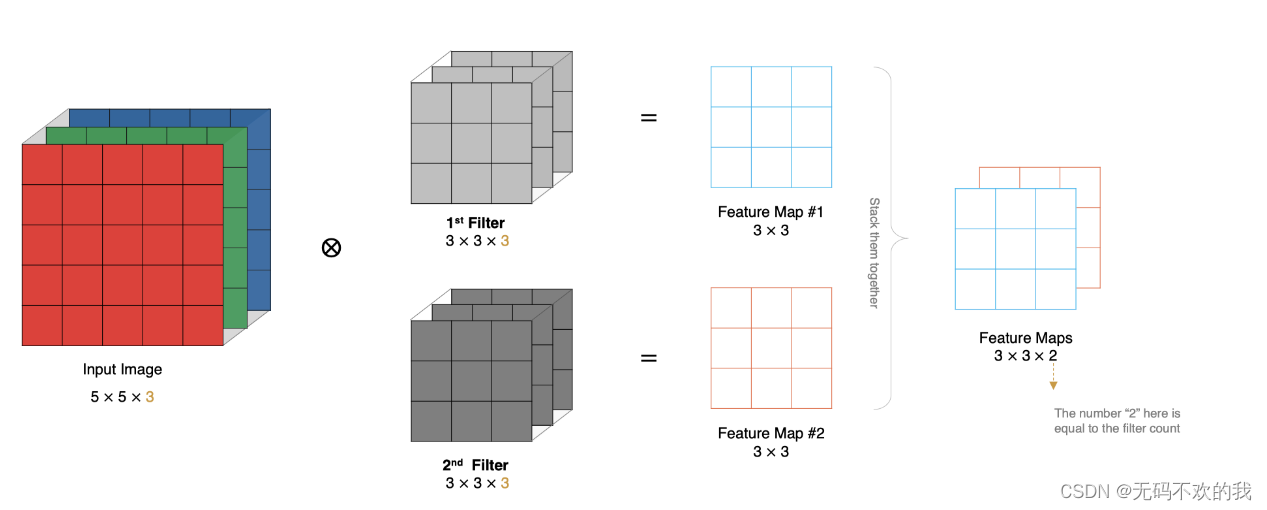
例如下图所示，输入图像有3个通道，同时有2个卷积核。对于每个卷积核，先在输入3个通道分别作卷积，再将3个通道结果加起来得到卷积输出。所以最后的输出特征图（ Feature Map）有两个通道（channel）。
所以对于某个卷积层，无论输入图像有多少个通道，输出图像通道数总是等于卷积核数量！

在这里插入图片描述

6 特征图大小

输出特征图的大小与以下参数息息相关：

size:卷积核/过滤器大小，一般会选择为奇数（因为尺寸为奇数的卷积核可以找到中心点），比如有1 * 1， 3 * 3， 5 * 5 ，一般选用尺寸较小的卷积核，比如3 * 3的核使用的最多，因为核越大所包含的参数就越多。
padding：零填充的大小（这里的大小指的是原始图像单侧外围厚度，比如下例中padding大小为1）
stride:步长

那计算方法如下图所示：

在这里插入图片描述

注意：

上面的D1是输入特征图的通道数；D2是输出特征图的通道数，它等于卷积核（Filter）的数量
上面公式最终的计算结果是向下取整

例如：输入特征图为5x5，卷积核为3x3，外加padding 为1，步长为1，则其输出特征图尺寸为：
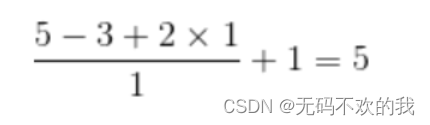
在这里插入图片描述
如果想让卷积前后的特征图的尺寸不发生变化，那么可以设置 padding=( F-1 )/2，并且步长stride=1

7 pytorch中对应的API

nn.Conv2d(in_channels,out_channels,kernel_size,stride=1,padding=0,dilation=1,groups=1,bias=True,padding_mode='zeros')

功能：对多个二维信息(图像)进行二维卷积

in_channels: 输入通道数
out_channels: 输出通道数，等价于卷积核个数
kernel_size: 卷积核尺寸
stride: 步长
padding: 填充个数，加入padding的主要作用是保持输入输出图像的尺寸不变
dilation: 空洞卷积大小
groups: 分组卷积设置，它常用于模型的轻量化
bias: 偏置

8 3D卷积

上面所讲的内容都是常规的2D卷积，本节着重讲解一下3D卷积。
在讲解3D卷积之前，我们先了解一下3D图像，3D图像比2D图像多了个一个维度，除了宽和高之外还有深度。这里的深度其实就是将相同尺寸的多张图片堆叠在一起，如果堆叠n张图片，那么深度就是n

3D图像通常是由多帧（单/多通道）的frame-like数据（视频帧），所以它的深度其实代表的就是帧数

所以2d图像的输入或输出shape=[B,C,H,W]，3d图像的输入或输出shape=[B,C,D,H,W]，其中D就是depth(深度)，这里的depth就是要堆叠出多少张图片。

如下图所示，将3张单通道的图片堆叠在一起(D=3)，处理这样的数据就需要一个3D卷积核，3D卷积核也有对应的深度，比如下图中的3D卷积核深度是2，也就是说它每次要扫描2张图片
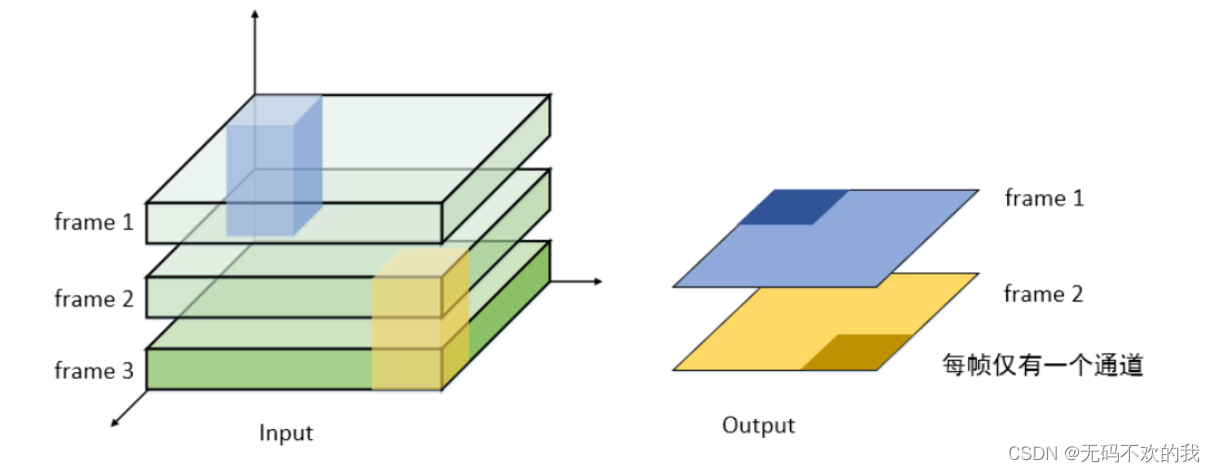
在这里插入图片描述
再如下图所示，将5张单通道的图片堆叠在一起(D=5)，处理这样的数据就需要一个3D卷积核，3D卷积核也有对应的深度，比如下图中的3D卷积核深度是2，也就是说它每次要扫描2张图片

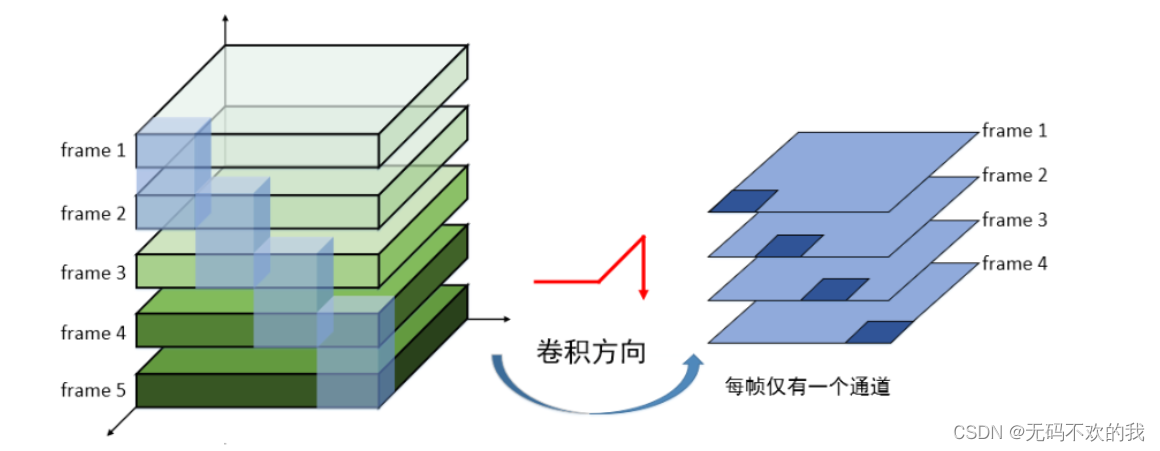
3D卷积计算过程：

3D convolution的使用场景一般是多帧（单/多通道）的frame-like数据（视频帧），且输出也是多帧，依次对连续k帧的整个通道同时执行卷积操作；3D卷积在执行时不仅在各自的通道中共享卷积核，而且在各帧（连续k帧）之间也共享卷积核（2D卷积在执行时是在各自的通道中共享卷积核）

假设现在有一个3帧的画面，且每一帧有2个通道，卷积核的shape=[D,H,W]=[2,3,3]，步长为1，padding=0，它的计算过程如下:
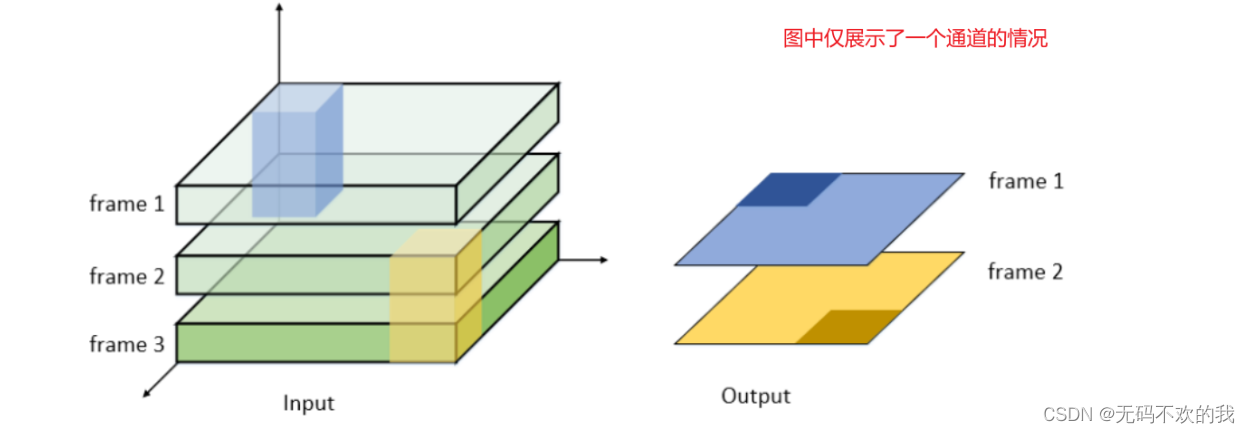
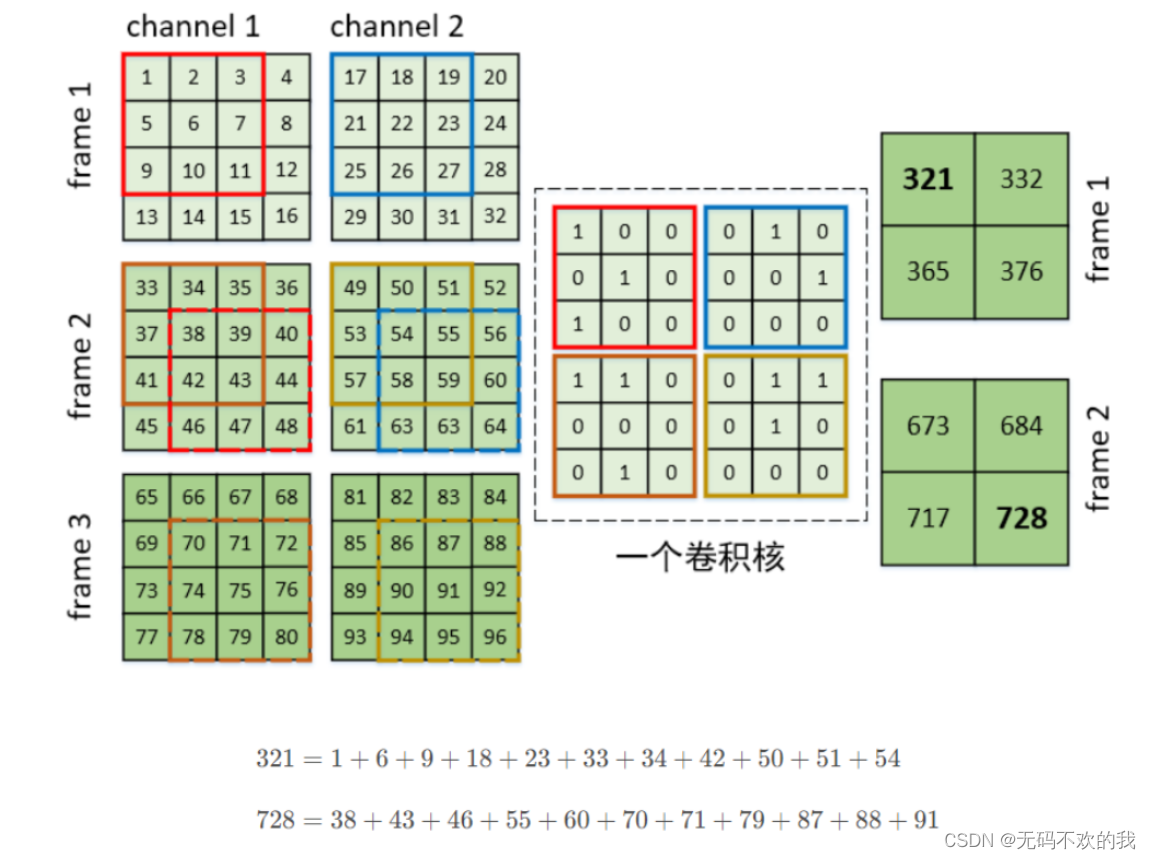
在这里插入图片描述

pytorch中对应的API：

torch.nn.Conv3d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

Conv3d和Conv3d的参数含义是完全相同的，如下所示：

in_channels: 输入通道数
out_channels: 输出通道数，等价于卷积核个数
kernel_size: 卷积核尺寸
stride: 步长
padding: 填充个数，加入padding的主要作用是保持输入输出图像的尺寸不变
dilation: 空洞卷积大小
groups: 分组卷积设置，它常用于模型的轻量化
bias: 偏置

代码演示：

示例1

#3D卷积的用法
import torch
import torch.nn as nn# 随机输入，它的shapo=[B,C,D,H,W]=[32,3,6,224,224]
net_input = torch.randn(32, 3, 6, 224, 224)#卷积层输入通道数是3，输出通道数是64
# 3D卷积核的shape=(D,H,W)=(3,3,3)，由于D=3，所以卷积核每次会同时处理三张图片。D,H,W三个维度的步长都是1
conv = nn.Conv3d(3, 64, kernel_size=3, stride=1, padding=1)
net_output = conv(net_input)
print(net_output.shape) #输出结果如下，shape=[B,C,D,H,W]=[32, 64, 5, 112, 112]，相当于每一个维度上的卷积核大小都是3，步长都是1，pad都是1
torch.Size([32, 64, 6, 224, 224])

示例2

# 3D卷积核的shape=(D,H,W)=(2,3,3)，由于D=3，所以卷积核每次会同时处理2张图片。D,H,W三个维度的步长分别是2，3，3
conv = nn.Conv3d(3, 64, (2, 3, 3), stride=(1, 2, 2), padding=(0, 1, 1))
net_output = conv(net_input)
print(net_output.shape) 
#输出结果
torch.Size([32, 64, 5, 112, 112])