一、数学描述
1. 定义
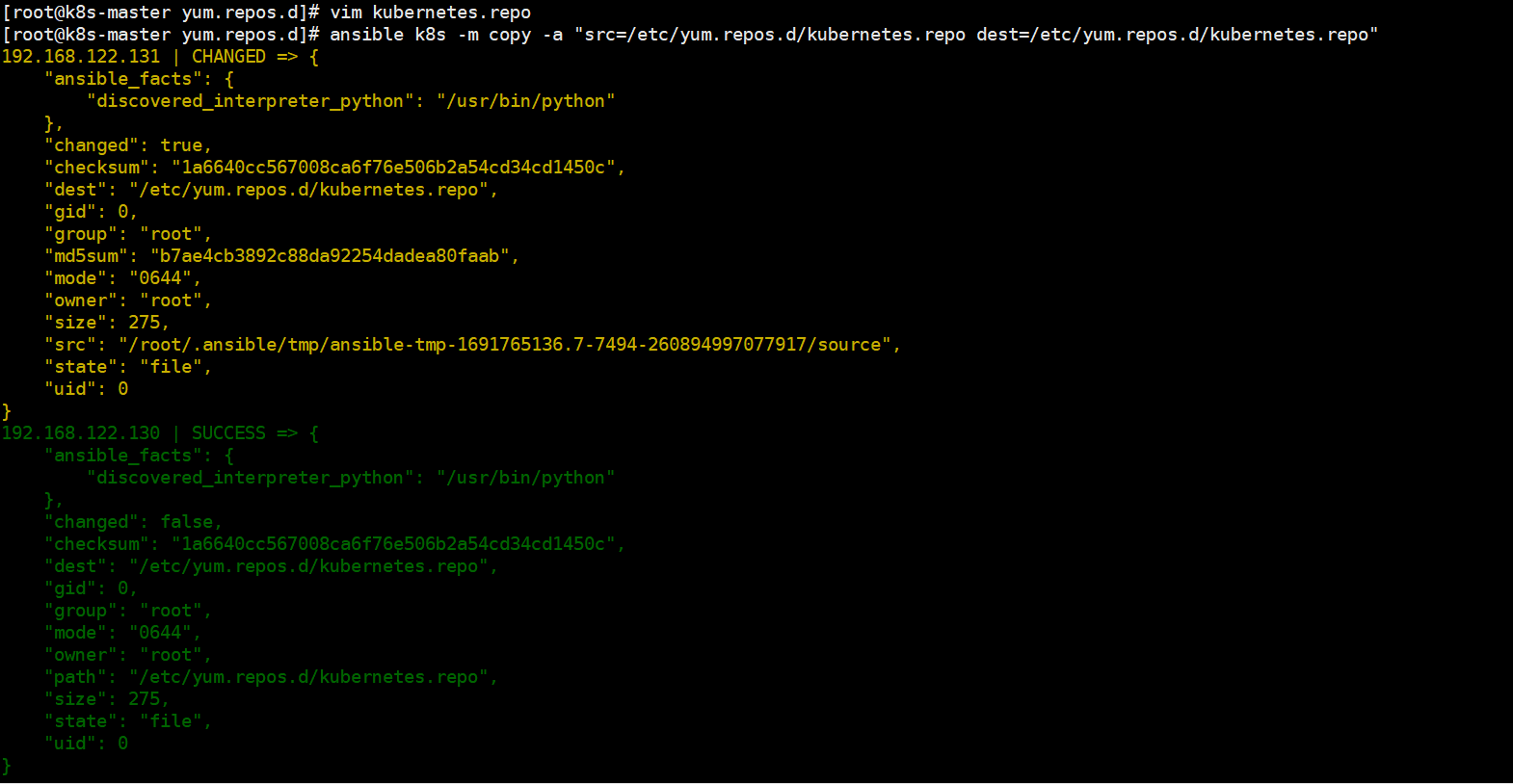
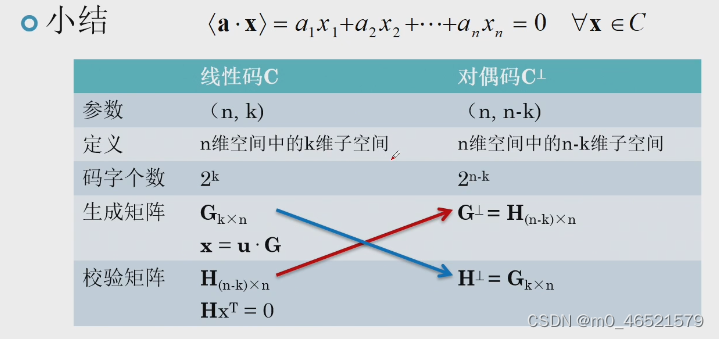
(n, k)线性分组码,n是码长,k是信息位数,n-k是校验位数,k/n是编码速率。
2. 生成矩阵

设是
维的信息矢量,
是
维的生成矩阵,
是编码后的
维码字,则

3. 系统线性分组码
如果线性分组码,码字
的高
个分量恰好等于信息矢量
的
个分量,则
码
称作系统码。

4. 对偶码

5. 校验矩阵


6. 定理1
如果(n, k)系统码C的生成矩阵G=(A | I)
则其校验矩阵为
二、q进制对称信道上的译码
1. 汉明重量与汉明距离
汉明重量:码字x的汉明重量是它的非零分量的个数,记作
汉明距离:码字x和y之间的汉明距离是它们不相同分量的个数,记作
码间最小距离等于其非零码字的最小重量。
2. q进制对称信道

3. 译码准则
最大似然概率译码准则

选择的x应使最小
4. 伴随式


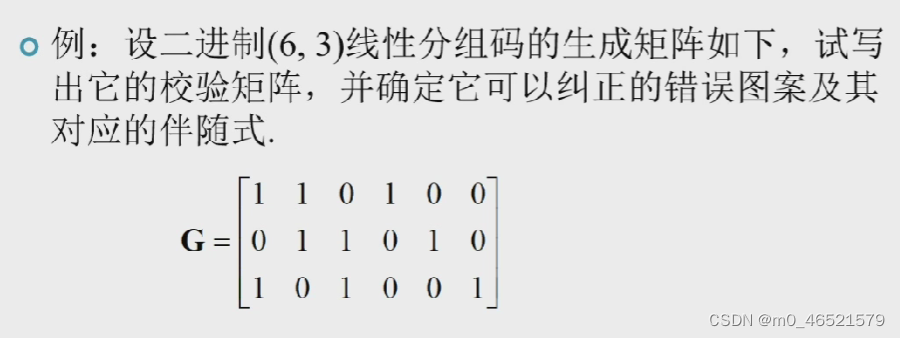
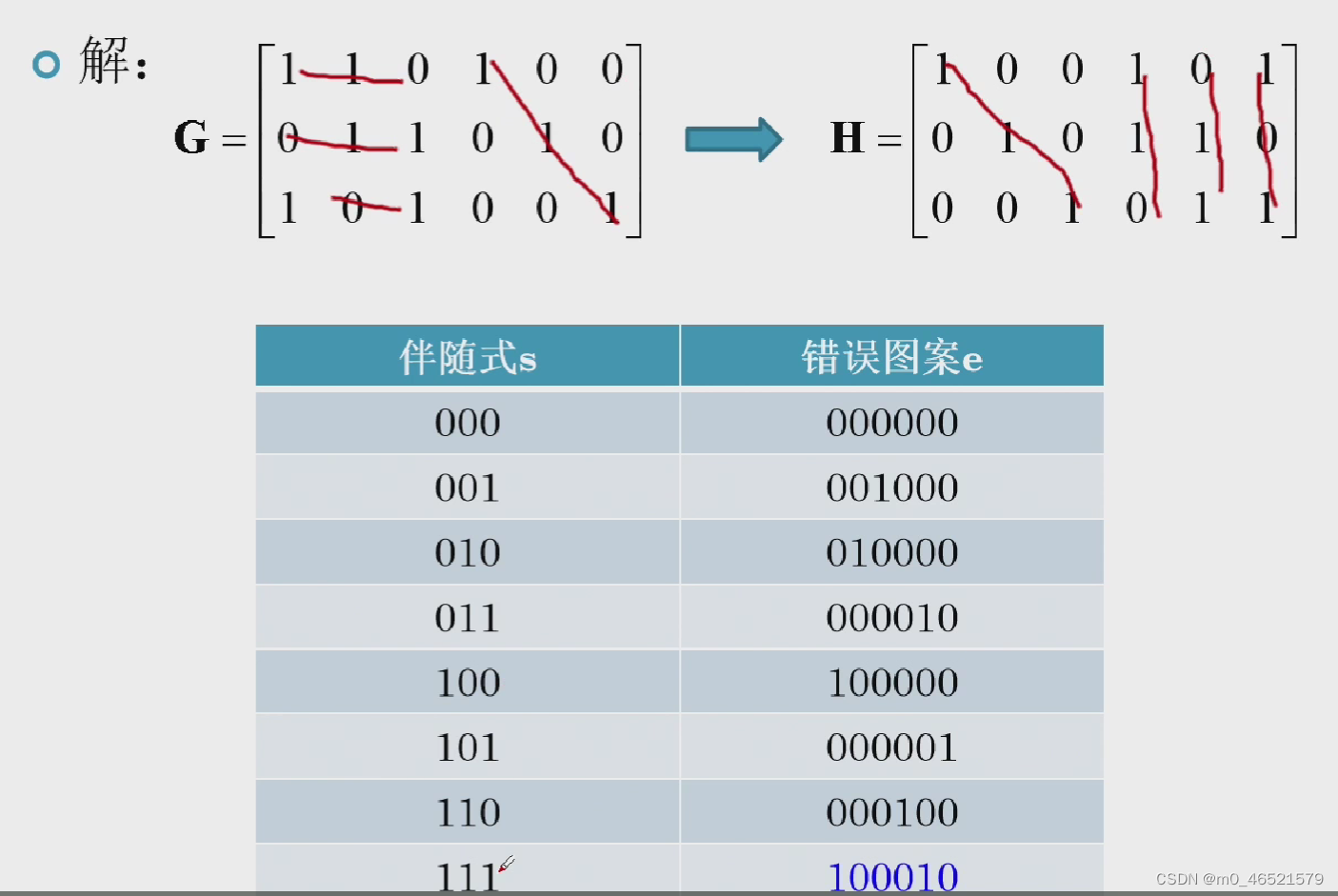


三、码间最小距离与纠错能力
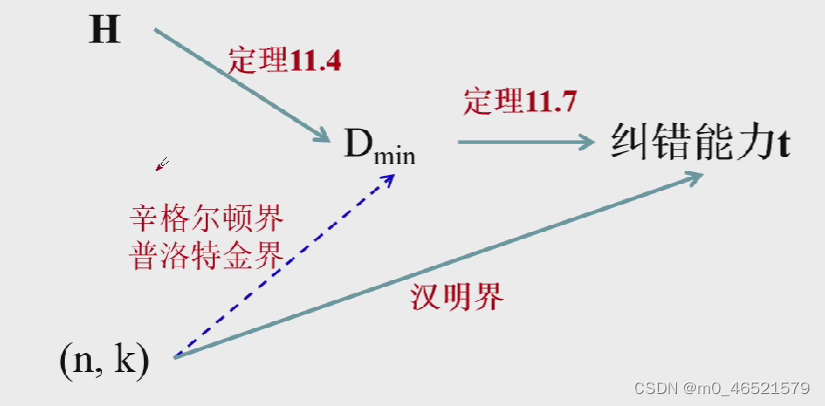
1.  与校验矩阵的关系
与校验矩阵的关系
码C是GF(q)上(n, k)线性分组码,其校验矩阵H中线性相关列矢量组的最小数目等于及
。

2. 辛格尔顿界
任意(n, k)线性分组码的码间最小距离d_min满足不等式d_min <= n-k+1
3. 普洛特金界

4. 纠错能力与最小汉明距离之间的关系

5. 汉明界

四、重量枚举多项式及译码错误概率估计
线性分组码的纠错能力主要取决于码字之间的距离。
对于线性码只需要考虑全零码字与其它非零码字的距离,即非零码字的重量。
码字的重量分布是用重量枚举多项式来描述的,线性分组码的重量枚举多项式表示为