Single Particle Simulation
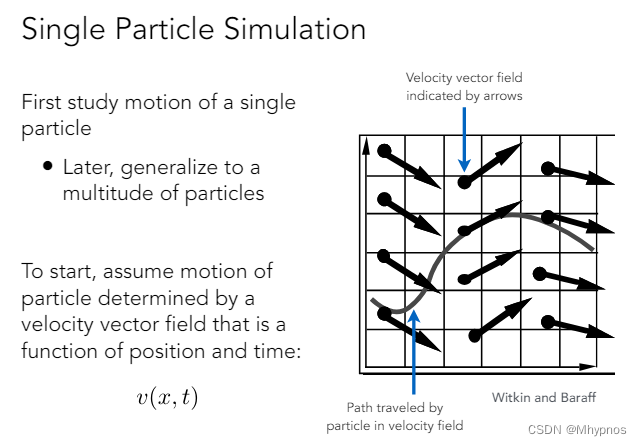
规定了任何一个物体任何时刻的速度,知道它的初始位置,求它某个时间后的位置?
如果一个物体是匀速直线运动,用初始位置加上速度和时间的乘积即可
如上图,如果想描述一个粒子在一个速度场(理想的情况:只要知道位置,就知道它这个时刻的速度)中如何运动
任何一个粒子在上面的速度场会沿着类似水流的方向往前走
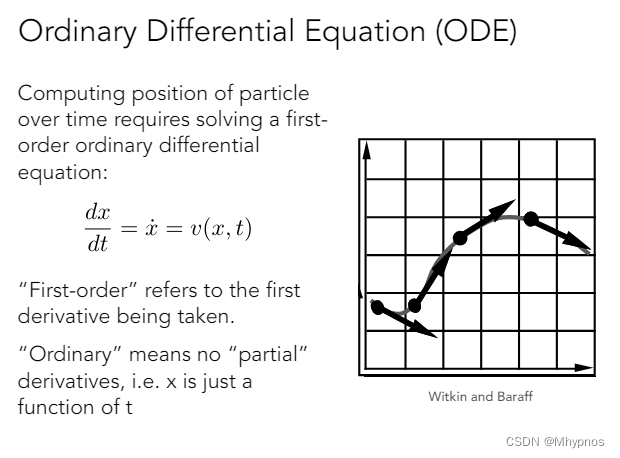
任何一个位置x和任何时间t,都知道有一个速度
一阶常微分方程ODE,只有对一个变量的微分/导数
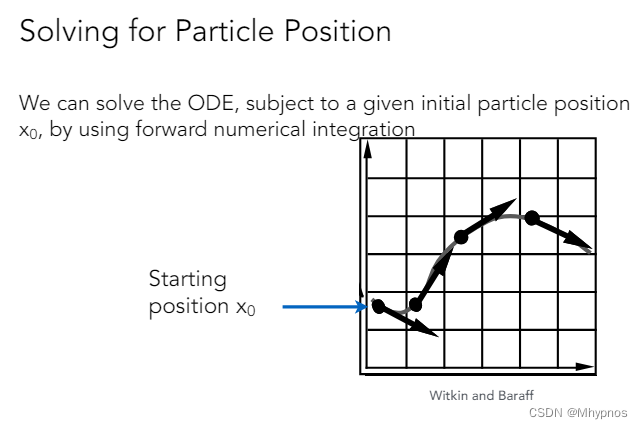
知道速度,一个起始位置,求任何时刻的位置

** Euler’s Method(欧拉方法)**
将时间细分成很多时间的小块,不断计算t+△t的位置
在t时刻有一个位置、速度和加速度,要算t+△t时刻的位置、速度和加速度
始终用上一个时刻的量去估计下一个时刻的量

欧拉方法有误差,会迅速的变得不稳定
通过减小△t来减小误差
用不同大小的步长(△t),△t分得越细,模拟就会越准越精确,如果越大(每次取一个速度,让它往前走很长一段),它就和实际的路线偏离得越多

不稳定:无论取多大的△t,它都会变得和实际结果相差无限远
如上图,不管取多大的步长,路线都肯定不会沿着螺旋形走,而且一定会离开这个螺旋形的速度场(可是事实上,粒子在一个螺旋形的速度场,一定会按照严格的圆周运动的)
一个像羽毛一样的速度场(实际上应该会按照一根曲线慢慢走到水平)(在信号与系统中这种情况叫正反馈,就是出现了一个问题后,这个问题会被无限的放大)

一切用数值方法解微分方程都会面临的问题
误差:误差其实问题不大,因为在每一步计算都会有误差,累积起来还是有误差。如果用的步长较小,就可以降低误差。对于图形学说,有时候模拟出来的误差问题也不大,因为图形学关注的是模拟看起来的效果,而不是物理上特别的真实
不稳定:更大的问题是不稳定,diverge(不管通过怎样的方法模拟得到的结果,最后都和实际的正确的结果差得越来越远)

车子撞上一辆摩托出现奇怪的翻滚的现象(在此不确定是否是不稳定造成的,但不稳定确实会出现这样的问题)
Combating Instability

中点法
自适应改变步长
隐式方法
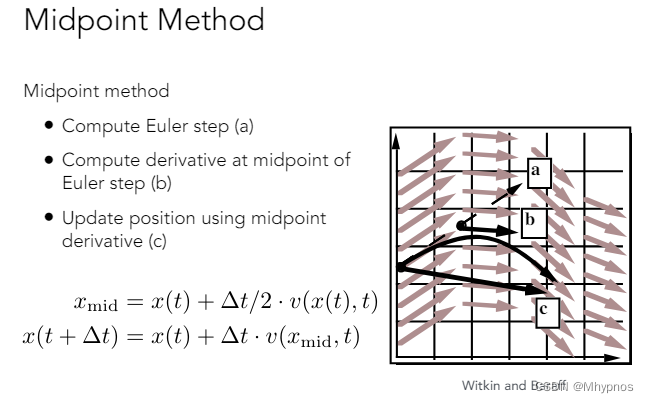
不希望欧拉方法在模拟的过程中让结果离得越来越远
- 一开始有一个位置和一个方向,可以直接用欧拉方法来模拟某个△t,让其先到达a
- 取原始点和a点之间的中点b,考虑它所在的速度
- 再回到原始的出发点,应用b点的速度来重新再算一遍欧拉方法,到达c点
仍然用的欧拉方法,只不过用2次,第一次为了得到中点的速度,第二次用中点的速度再算一次欧拉方法

中点法比欧拉方法准确,是因为多了一个二次的项,也就是说通过中点法模拟出了抛物线的轨迹
可以认为原本的欧拉方法是局部线性的估计模型,而中点法作为修正的欧拉方法其实就算出了局部的二次的模型,所以比一次的模型准确
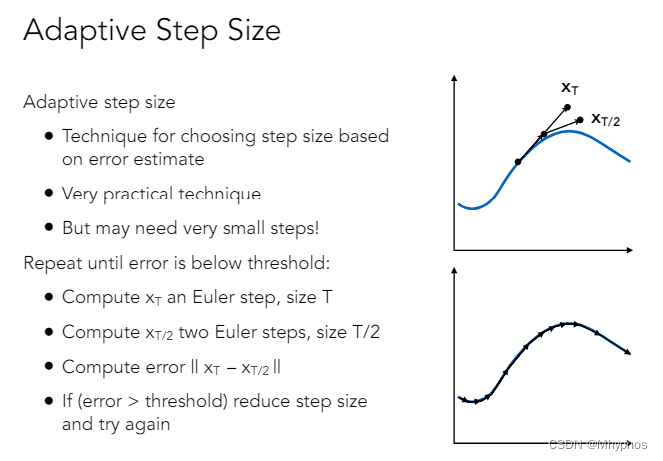
自适应改变步长
先正常一个△t算出新的位置XT,将时间减半,得到2个△t,算2遍,从原始点先用△t/2算到一个位置,再使用△t/2再算一次,到达XT/2
如果XT和XT/2这2个点差得挺远,这就意味着将△t分成2部分分别考虑这样做会更准确,那就应该考虑△t/2;如果差得不远,就没必要再分下去
是否将这个点划分成2部分取决于上面2个点差得远不远+
结果:会得到在不同位置选用不同△t来做计算

隐式欧拉方也叫backward methods
用的永远是下一个时间的速度和加速度(一开始并不知道)来更新此时的

最后要解方程组,解出一个位置和速度
如果速度和加速度不是按照简单的线性方法叠加的,就不好解。
认为在这一时刻位置知道, 以及下一时刻加速度知道。只需要解下一时刻的位置和速度。
可以用求根公式(如牛顿法),虽然比之前数值的解法要慢很多,但隐式的方法可以提供更好的稳定性

如何定义一个方法是稳定的?以及它有多么稳定?
通常对于数值方法会定义2个概念来衡量稳定性:
local truncation error:局部的截断误差(也就是每一步(△t)会产生多少误差)
total accumulated error:每一步累积起来的误差
正常情况下研究这2个数是没有意义的,但是应该研究它们的阶(它们和我们取的△t的关系)
隐式的欧拉方法是一阶的:
局部误差是O(h²)
全局误差是O(h)(如果把h减小一半,就期望得到的误差也会减小一半)
h表示取的步长△t
所以阶数越高越好,因为减小h,误差可以成指数倍的减小

龙格库塔方法是一类解常微分方程ODE方法,特别是非线性的情况
RK4方法是应用最广泛的(四阶的方法)
解决的方法和欧拉方法是一样的:有一个一阶导数,某个量和时间和位置有关,并且有一个初始情况
更新的时候稍微有点不一样:用上一帧的位置用△t(式中的h)乘以某个平均值来更新
4个值是不同位置和不同时间在速度场中的值

非物理的方法
只通过调整它的不同位置,使得它最后能够满足某种限制
有时,不是基于物理的方法是很好用的(比如作业8中,可以认为弹簧确实是弹簧,但只要它被拉开了某个位置后,可以通过非物理的方法直接改变它的位置,使其立刻回到原状。可以认为它是一个劲度系数无限大的弹簧)
优点:实现快、简单
缺点:有时不能保证能量守恒的性质(因为不是基于物理的)(比如应用在绳子模拟器上,这个绳子会很快停下来,会有很大的能量损失)
Rigid Body Simulation

刚体不会发生形变,它会让内部所有的点都按照同一种方式去运动(其实一个刚体的运动就是一个粒子的运动,只不过在刚体的模拟中会更多的考虑其他的物理量)
如上图,一个刚体的位置、朝向(旋转的角度)、速度、角速度(旋转有多快)分别对时间求导后得到速度、角速度、加速度、角加速度
使用欧拉方法等数值方法可以求出任意一个时间t之后,刚体对应位置和旋转
Fluid Simulation

通过模拟形成整个水的体积的小球的位置,来模拟整个水浪花的运动
- 认为整个一个水体是由很多不可压缩的刚体小球组成的
- 认为水在任何地方都是不可压缩的,即在任何时刻任何位置的密度都是一样的
- 给定任何一个时刻这些小球它们分布,都可以知道任何一个地方的密度。如果有任何一个地方的密度变得和水一开始平静的时候的密度不一样,那就需要通过移动小球的位置把这个密度修正过来
- 为了做上面的修正,需要知道任何一个点它的密度对所有的小球位置的梯度/导数(任何一个点,如果周围有一圈粒子都会影响它的密度,如果移动任何一个粒子,都会让它的密度发生一定的改变,那就是密度对于这一个粒子的导数)
就是机器学习中的梯度下降

在物理模拟中模拟大规模的物质用到的2个基本思路:
拉格朗日方法,俗称质点法:模拟水是认为水是由很多圆形的小水滴组成,挨个模拟小水滴。如上图,如果模拟一群小鸟的移动,就关注某一只
欧拉方法,俗称网格法:和解常微分方程的欧拉方法不是一回事。这里指如何去看待模拟的一系列大规模的物体。将整个空间分成不同的网格,不管网格中的东西是出去了还是进来了,只考虑这个网格随着不同的时间是如何变化的。如上图,分成了网格,就知道时间t应该显示黑色的鸟,时间t-1应该显示蓝色的鸟

物质点方法,既考虑欧拉,又考虑朗格朗日方法
首先认为这些不同的粒子都具有某些材质属性(粒子有质量、粘度等等,都存在点上)
融化的过程在网格中做
再将格子上的信息写回不同的粒子上去
作业
根据题目描述,以及代码看出,mass就是绳子的质点,spring是两个质点直接的弹簧
实现完构造函数,可画出绳子

显示欧拉,绳子飞了

半隐式欧拉:

16个质点

32仿真步数

128仿真步数
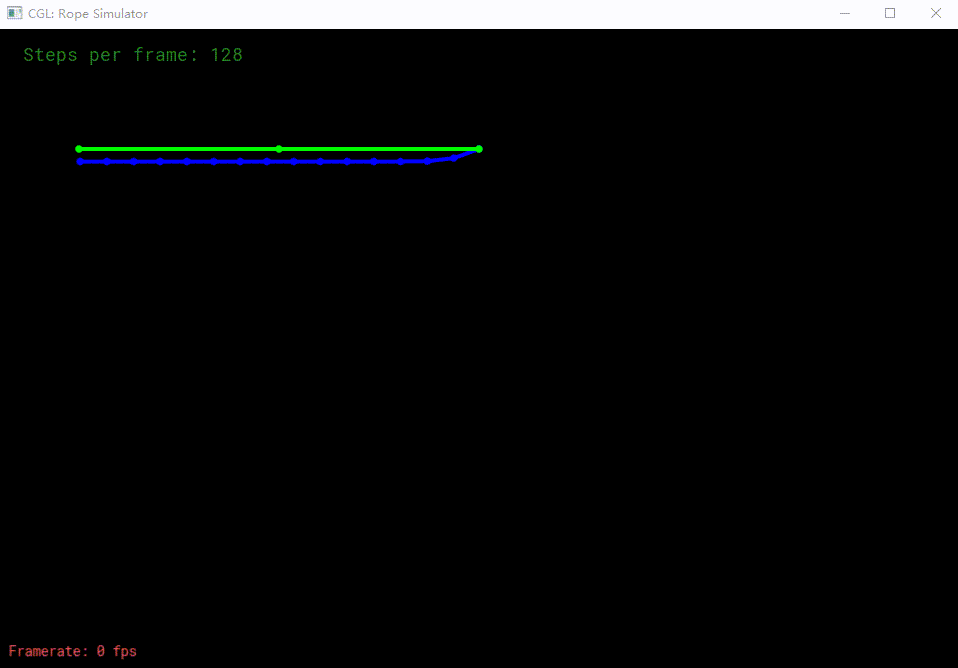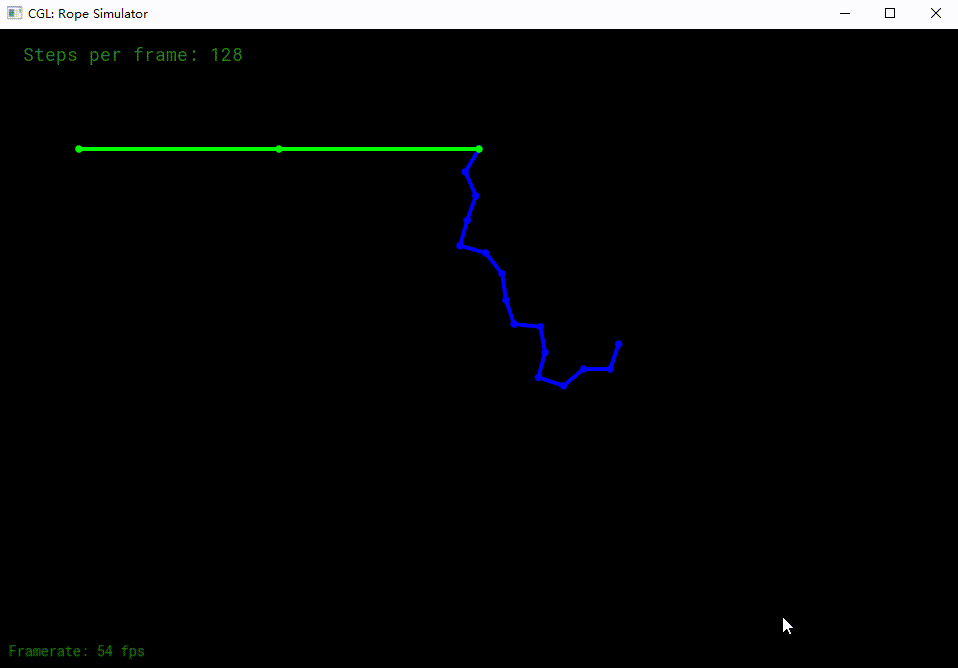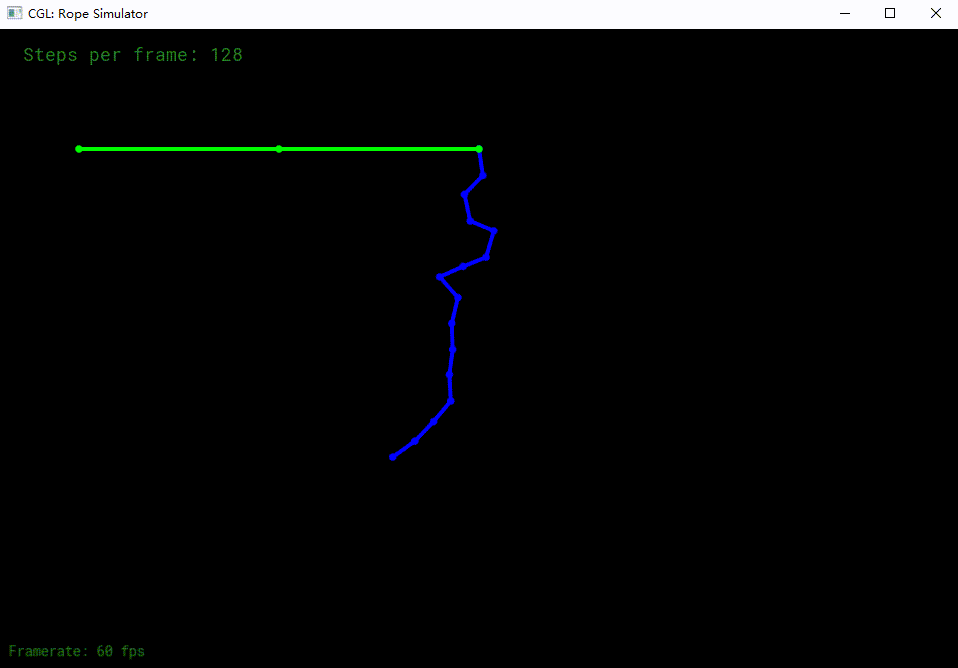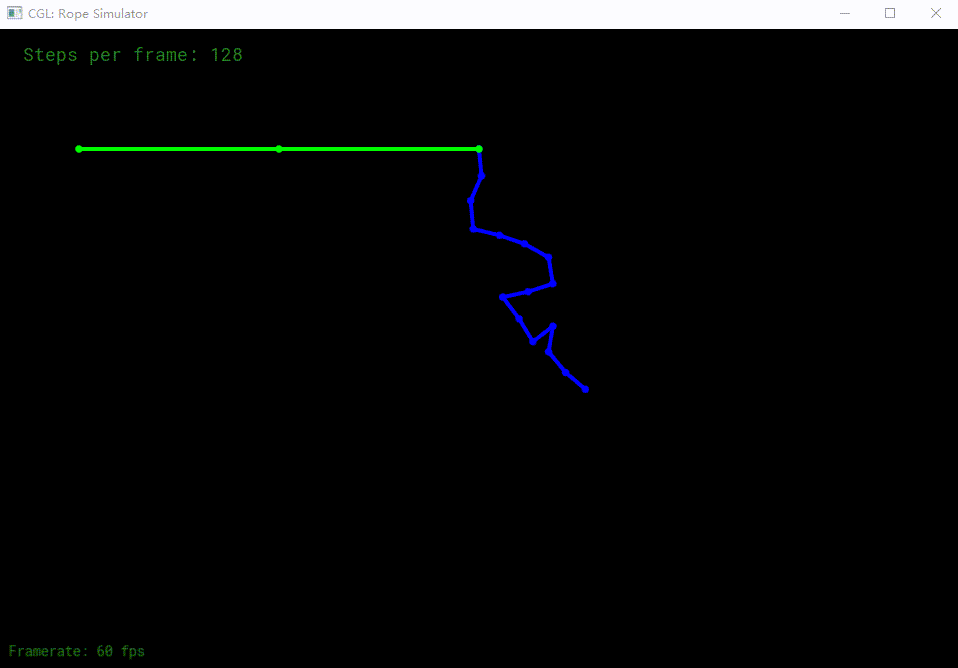
显示verlet

verlet加入阻尼
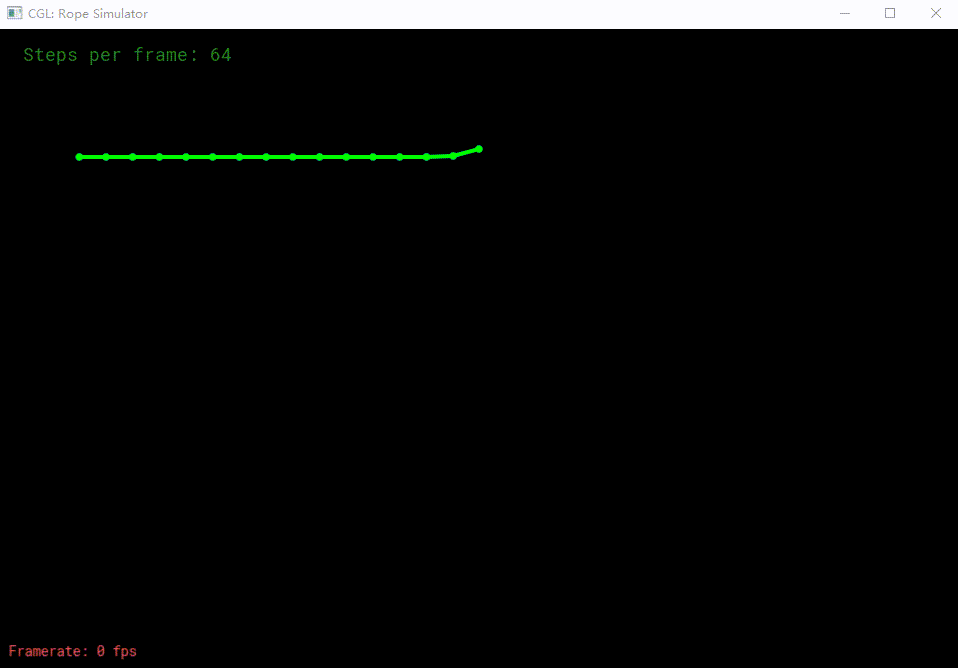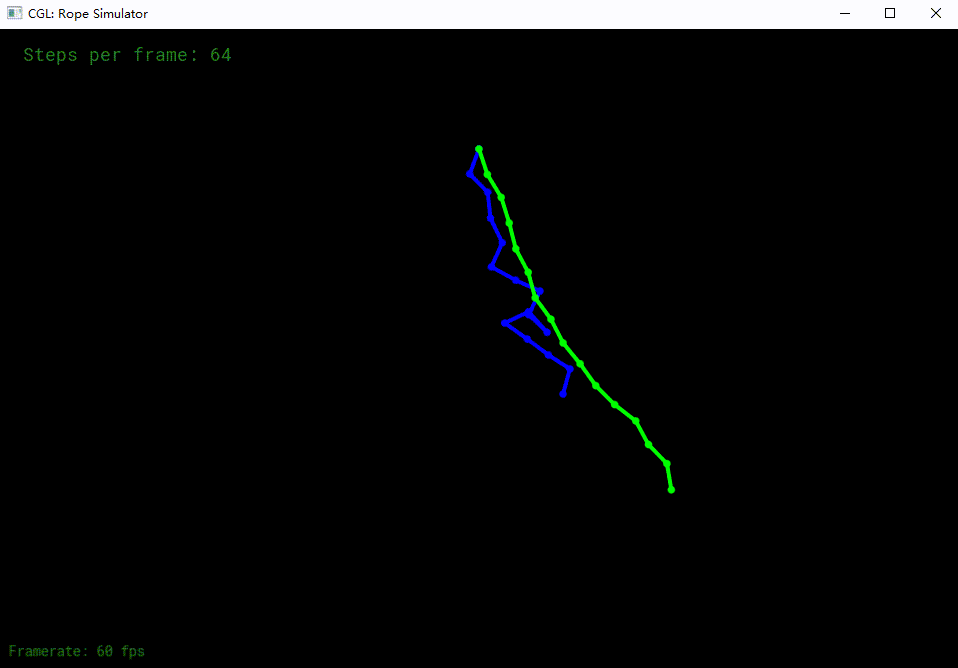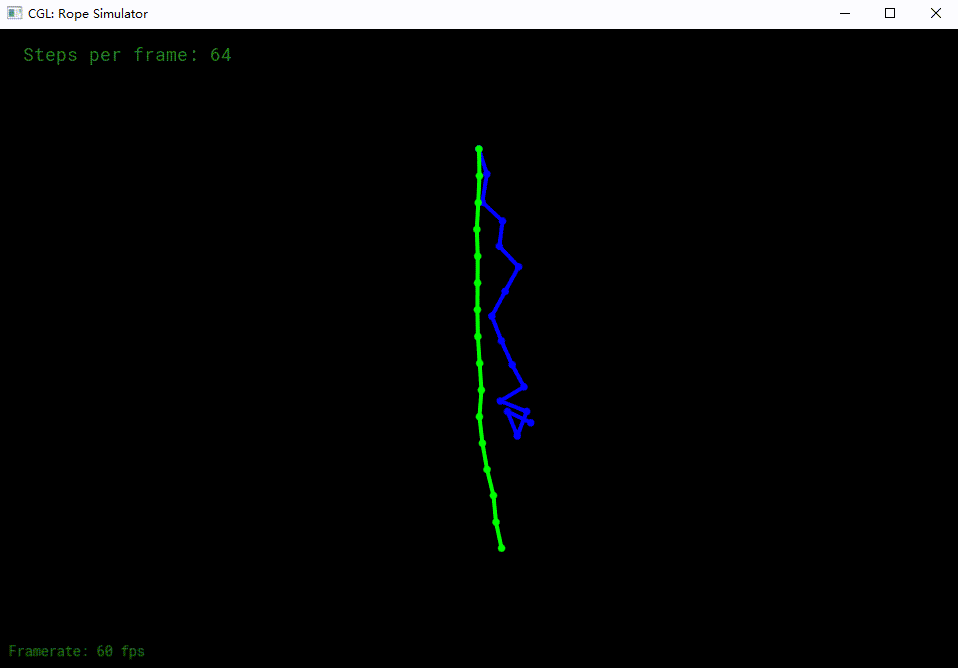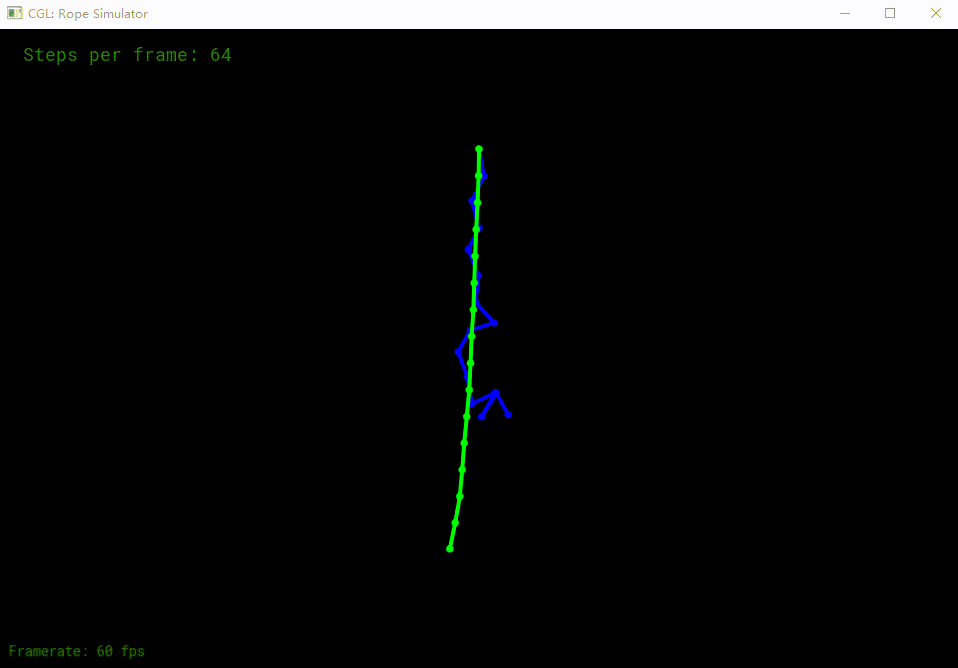
半隐式欧拉加上阻尼半隐式欧拉阻尼

更多步长,阻尼导致更快稳定

github作业地址