STL 总结-编程知识

STL

在 C++ 标准模板库（STL）中，主要包含了一系列的容器、迭代器、算法、函数对象、适配器。

容器

容器是用于存储数据的类模板。STL 容器可以分为序列型容器、关联型容器和链表型容器三类：
序列型容器：vector、deque、array。
关联型容器：set、map、multiset、multimap。
链表型容器：forward_list、list、unordered_set、unordered_map、unordered_multiset、unordered_multimap。

迭代器

算法

STL 算法通过迭代器与容器进行交互，进行数据处理和操作。
非修改序列算法：find、count。
修改序列算法：copy、move、transform。
排序算法：sort、stable_sort。
二分搜索算法：lower_bound、upper_bound。
数值算法：accumulate、inner_product。

函数对象

STL 中的函数对象是实现了 operator() 的对象，常用于算法中作为策略或条件表达式。包括算术运算类、关系运算类、逻辑运算类。

适配器

适配器用于修改容器或迭代器的接口。
容器适配器：stack、queue、priority_queue。

一、vector

vector 底层实现原理

底层实现了一个动态数组。
类构成：
- 以 protected 的方式继承自 _Vector_base，基类的 public 在子类中将变为 protected，其他的权限不变。
```
class vector : protected _Vector_base<_Tp, _Alloc> {}
```
- _Vector_base 组成：
  - _M_start：指向第一个元素的位置 → vec.begin()。
  - _M_finish：指向最后一个实际存储元素的下一个位置 → vec.end()。
  - _M_end_of_storage：指向为 vector 所分配的内存块的末尾之后的第一个位置。
  - 从 _M_start 到 _M_finish 之间的内存是 vector 实际使用的空间 → vec.size()。
  - 从 _M_start 到 _M_end_of_storage 之间的内存是 vector 可以用来存储元素的空间 → vec.capacity()。
  - 从 _M_finish 到 _M_end_of_storage 之间的内存是已经分配好可以随时使用的，但是目前未使用的。
```
template<typename _Tp, typename _Alloc>
struct _Vector_base
{struct _Vector_impl_data{pointer _M_start;pointer _M_finish;pointer _M_end_of_storage;...}...
}
```
构造函数：
- 无参构造函数：不会申请动态内存，保证性能优先。
- 初始化元素个数的构造函数：一次性申请足够的动态内存 → 避免多次申请动态内存，影响性能。
插入元素：
- 往最后位置插入：
  - 检查空间是否需要动态分配内存，是否需要扩容（_M_finish 是否等于 _M_end_of_storage）。
  - 插入到最后：push_back()、emplace_back() → ++_M_finish。
- 往其他位置插入。
  - 检查空间是否需要动态分配内存，是否需要扩容。
  - 将插入位置之后的元素往后平移一位，然后插入元素：insert()。
删除元素：不会释放现有已经申请的内存。
- 删除最后一个元素 pop_back()：_M_finish 往前移动一位（--_M_finish）。
- 删除其他元素 erase()：将待删元素之后的元素向前平移一位，_M_finish 往前移动一位。
读取元素：返回的是具体元素的引用。
- 操作符[]。
- at()：比操作符[] 多了一个检查越界的动作，越界后会抛出错误。
修改元素：vector 不支持直接修改某个位置的元素。
- 通过读取元素，获取引用，然后进行修改。
- 先删除后插入。
释放空间：
- swap() 交换一个空容器。
```
std::vector<int>().swap(vec); 
```
- 先 clear()，然后 shrink_to_fit() → 释放掉未使用的内存。

vector 内存增长机制

特点：
- 内存空间只会增加不会减少。
- vector 的内存是连续的。
- 不同平台的增长方式不一样，Linux 下是以翻倍的方式进行增长。
增长特征：
- 无参构造，连续插入一个，增长方式：1、2、4、8 …
- 有参构造，连续插入一个，增长方式：10、20、40 …
增长时的具体操作：
- 此时 _M_finish == _M_end_of_storage，将内存空间大小翻倍并产生新的内存空间。
- 将容器原来内存空间中的数据复制到新的内存空间中。
- 释放容器原来的内存空间。
- 插入新元素。
注意：vector 中的元素为指针时，不会调用析构函数，需要手动释放内存。

vector 中 reserve 和 resize 的区别

共同点：
- 调用它们，容器内原有的元素不受影响。
- 它们都起到增加的作用，对于缩小操作直接无视。
区别：
reserve 能增加 vector 的 capacity，但是它的 size 不会改变。
resize 既增加了 vector 的 capacity，又增加了 size。
应用场景：
- reserve 用来避免多次内存分配。
- resize 确保操作符[] 和 at() 的安全性。

vector 中的元素类型为什么不能是引用

引用的特征：
- 引用必须要进行初始化，不能初始化为空对象，初始化后不能改变指向。
- 引用是别名，不是对象，没有实际的地址，不能定义引用的指针，也不能定义引用的引用。
不能为引用分配内存 → 不能定义引用的指针。
push_back() 传入左值时会调用拷贝构造函数 → 不能定义引用的引用。
基于操作符[] 和 at()，将会获取引用的引用 → 不能定义引用的引用。

vector 中 push_back 和 emplace_back 的区别

push_back 如果传入的是左值，会调用拷贝构造函数；如果传入的是右值，会调用移动构造函数。

emplace_back 利用传入的参数在容器内存中直接构造元素，而无需首先创建临时对象再将其拷贝或移动到容器中，它使用 forward 完美转发将参数直接传递给元素的构造函数。

vector<string> vec;// 使用 push_back 添加字符串
string str = "Hello";
vec.push_back(str);                   // 调用拷贝构造函数
vec.push_back(string("World"));       // 调用移动构造函数// 使用 emplace_back 添加字符串
vec.emplace_back("Hello, World");     // 直接在容器中构造字符串

vector<string> vec;string hello = "Hello";
// 这里会调用拷贝构造函数，因为传递的是一个现有的 string 对象
vec.emplace_back(hello);// 这里直接在容器中构造一个新的 string，不调用拷贝或移动构造函数
vec.emplace_back("World");

二、list

底层实现了一个双向循环链表。
类构成：
- 以 protected 的方式继承自 _List_base。
```
class list : protected _List_base<_Tp, _Alloc> {}
```
- _List_base → _List_impl → _List_node → _M_storage：存储具体的值。
- _List_node 继承自 _List_node_base → _M_next、_M_prev。
```
_List_node_base* _M_next;
_List_node_base* _M_prev;
```
构造函数：
- 不管如何构造，初始都会构建一个空节点 dummyHead。
- 空节点用来表示整个双向循环链表。
迭代器：
- ++ 往下移动指针 → _M_node = _M_node->_M_next。
- -- 向上移动指针 → _M_node = _M_node->_M_prev。
获取第一个元素：空节点的下一个节点 → this->_M_impl._M_node._M_next。
获取最后一个元素：空节点的上一个节点 → 先获取空节点 this->_M_impl._M_node，再 --。
插入元素：每插入一个元素，都临时为该节点分配内存，修改指向，size++。

在这里插入图片描述

三、deque

目的是实现双端数组，底层实现了一个双向开口的连续线性空间。
类构成：
- 以 protected 的方式继承自 _Deque_base。
```
class deque : protected _Deque_base<_Tp, _Alloc> {}
```
- _Deque_base → _Deque_impl：
  - _M_map：指针数组。
  - _M_map_size：_M_map 的容量。
  - _M_start：记录 _M_map 指针数组中首个连续空间的信息。
  - _M_finish：记录 _M_map 指针数组中最后一个连续空间的信息。
迭代器 _Deque_iterator：
- _M_cur：指向当前正在遍历的元素。
- _M_first：指向当前连续空间的首地址。
- _M_last：指向当前连续空间的尾地址。
- _M_node：指向 _M_map 指针数组中存储的指向连续空间的指针。
__deque_buf_size：连续空间中能容纳的元素个数；如果元素大小小于 512 字节，则能容纳 512 / 元素大小个元素，否则只能容纳一个元素。
_M_initialize_map：
- 创建 _M_map，最小为 8，并配置缓冲区。
- _M_start 和 _M_finish 指向中间的位置，方便公平地往上或者向下扩展空间。
push_back：
- 先看当前连续空间够不够，够就直接插入。
- 不够的话，再看 _M_map 空间够不够，够就生成新的连续空间。
- 不够的话，就生成新的 _M_map，把旧的_M_map 中的数据挪到新的 _M_map 中。
pop_back：删除当前连续空间的最后一个元素，如果当前连续空间没有数据了，则释放该连续空间。

在这里插入图片描述

四、vector、list、deque 使用场景

如果需要高效地快速访问（随机存取），并且不在乎插入和删除的效率，使用 vector。
如果需要大量地插入和删除，并且不关心快速访问（随机存取），使用 list。
如果需要快速访问（随机存取），并且关心两端数据的插入和删除，使用 deque。

五、priority_queue

底层实现了一个堆（Heap），堆是一种高效维护集合中最大或最小元素的数据结构。
- 大根堆：根节点最大的堆，用于维护和查询 max。
- 小根堆：根节点最小的堆，用于维护和查询 min。
- 堆是一棵树，并且满足堆性质：
  - 大根堆任意节点的关键码 $\geq$ 它所有子节点的关键码（父 $\geq$ 子）
  - 小根堆任意节点的关键码 $\leq$ 它所有子节点的关键码（父 $\leq$ 子）
底层容器：默认是 vector，也可以使用 deque。

选择容器的前提是容器要提供这三个接口：

front()。
```
top() const {return c.front();
}
```

push_back()。

push(const value_type& __x) { c.push_back(__x); 
}

pop_back()。

pop() {std::pop_heap(c.begin(), c.end(), comp);c.pop_back();
}

STL 对堆结构提供的接口：
- $priority\_queue$ 默认是大根堆，比较器为 std::less<>。
- make_heap(first, last, compare)：根据 compare 构建堆。
- push_heap(first, last, compare)：添加元素，并重新构建堆。
- empty()。
- size()。
- top()。
- push()。
- pop()。
二叉堆是堆的一种简易实现，本质上是一棵满足堆性质的完全二叉树。
二叉堆的实现：
- 二叉堆一般使用一个一维数组来存储，利用完全二叉树的节点编号特性。
- 假设第一个元素存储在索引（下标）为 $1$ 的位置：
  - 索引为 $p$ 的节点的左孩子的索引为 $p * 2$ 。
  - 索引为 $p$ 的节点的右孩子的索引为 $p * 2 + 1$ 。
  - 索引为 $p$ 的节点的父亲的索引为 $p /2$ （下取整）。
二叉堆的操作：
- 插入（ $p u s h$ ）：
  - 新元素一律插入到数组 $h e a p$ 的尾部。
    - 设插入到索引 $p$ 的位置。
  - 然后向上进行一次调整（ $\ Up$ ）。
    - 若已到达根，停止。
    - 若满足堆性质（ $\leq heap[p/2]$ ），停止。
    - 否则交换 $h e a p [p]$ 和 $h e a p [p /2]$ ，令 $p = p /2$ ，继续调整。
  - 时间复杂度： $O (l o g n)$ 。
- 取出堆顶（ $p o p$ ）：
  - 把堆顶（ $h e a p [1]$ ）与堆尾（ $h e a p [n]$ ）交换，删除堆尾（数组最后一个元素）。
  - 然后从根向下进行一次调整（ $\ Down$ ）。
    - 每次与左、右子节点中较大的一个比较，检查堆性质，不满足则交换。
    - 注意判断子节点是否存在。
  - 时间复杂度： $O (l o g n)$ 。

二叉堆代码：

struct Node {int key;ListNode* node;Node(int key, ListNode* node) : key(key), node(node) {}
};class BinaryHeap {
public:BinaryHeap() {// 从 1 开始存, 0 位置存一个无意义的值heap.push_back(Node(0, nullptr));}bool empty() { return heap.size() == 1; }Node getMin() { return heap[1]; }void insert(const Node& node) {heap.push_back(node);heapifyUp(heap.size() - 1);}void deleteMin() {heap[1] = heap[heap.size() - 1];heap.pop_back();heapifyDown(1);}private:void heapifyUp(int p) {while (p > 1) {if (heap[p / 2].key > heap[p].key) {swap(heap[p / 2], heap[p]);p = p / 2;} elsebreak;}}void heapifyDown(int p) {int child = p * 2; // 要交换的节点while (child < heap.size()) {int other_child = p * 2 + 1; // 另一个节点if (other_child < heap.size() &&heap[other_child].key < heap[child].key) {child = other_child;}if (heap[p].key > heap[child].key) {swap(heap[p], heap[child]);p = child;child = p * 2;} elsebreak;}}vector<Node> heap;
};

六、multiset

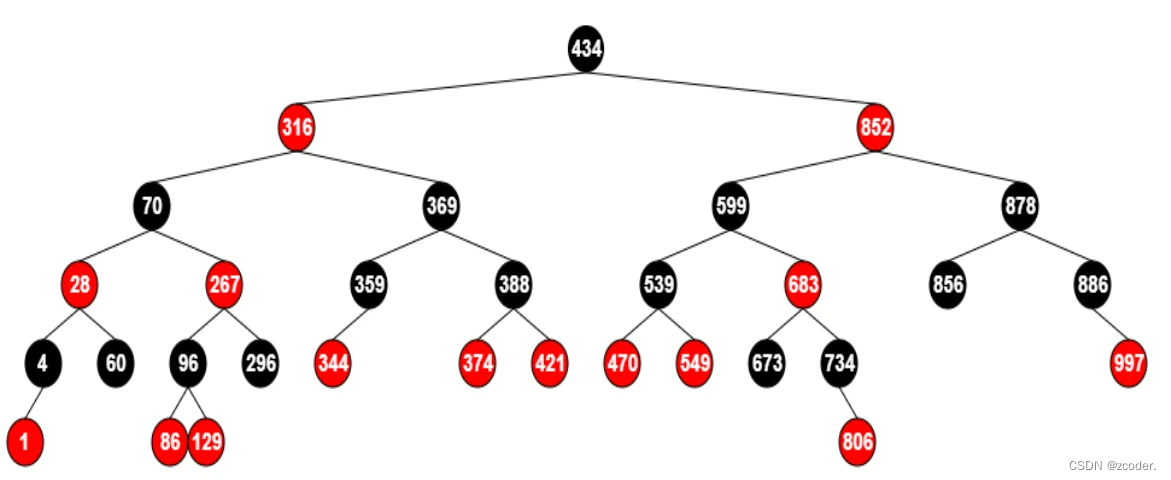
基于红黑树实现，允许键值重复的有序集合。
- map、set、multiset、multimap 都是基于红黑树实现。
红黑树性质：
- 红黑树是二叉排序树，中序遍历是顺序的。
- 每个节点是红色或者黑色。
- 根节点是黑色的。
- 所有叶子节点都隐藏，并且为黑色。
- 如果一个节点是红色的，则它的两个儿子都是黑色的 → 红色节点不相邻。
- 对每个节点，从该节点到其子孙节点的所有路径上的包含相同数目的黑节点 → 黑色节点高度一样。
  - 从根节点到叶子节点的最大深度和最小深度的关系是 2n - 1 : n
```
typedef struct _rbtree_node {struct _rbtree_node *parent;struct _rbtree_node *left;struct _rbtree_node *right;int key;     // 维持有序void *data;  // 节点额外信息unsigned char color; // 节点颜色
} rbtree_node;struct _rbtree {struct _rbtree_node root;struct _rbtree_node *nil; // 所有叶子节点都隐藏，并且为黑色
} rbtree;
```
STL 中红黑树的实现：
- 结构：
```
template<typename _Key, typename _Val, typename _KeyOfValue, typename _Compare, typename _Alloc = allocator<_Val> >
class _Rb_tree {}
```
  - _Key 是 key 的类型。
  - _Val 是节点数据的类型，key 和 data 的结合。
  - _KeyOfValue 是从 _Val 中取得 _Key 值的方法。
  - _Compare 是比较 key 的方法。
  - _Alloc 是分配内存的方法。
- 原理图：
- 重要接口：
  - _M_insert_unqiue：插入数据时，保证 key 唯一；插入相同节点会覆盖。
  - _M_insert_equal：插入数据时，允许 key 重复；插入相同节点会成为其的右孩子。

multiset 实现：

value_type 存储的就是 key，key 是不允许被修改的，所以 multiset 中的节点不允许被修改 → const_iterator。

insert 的时候调用的是 _M_insert_equal。

typedef _Rb_tree<key_type, value_type, _Identity<value_type>, key_compare, _Key_alloc_type> _Rep_type;

typedef _Key     key_type;
typedef _Key     value_type;

struct _Identity : public unary_function<_Tp, _Tp> {_Tp& operator()(_Tp& __x) const { return __x;} 
}

map 实现：

map 中的 data 是可以被修改的。

typedef _Rb_tree<key_type, value_type, _Select1st<value_type>,key_compare, _Pair_alloc_type> _Rep_type;

typedef _Key    key_type;
typedef _Tp     mapped_type;

struct _Select1st : public unary_function<_Pair, typename _Pair::first_type> {operator()(_Pair& __x) const { return __x.first;}
}

例子：

// <1, 2, 3>
set<int> s; // <1, 2, 2, 3>
multiset<int> ms;// <1->2, 3->2, 4->2>
map<int, int> m;// <1->2, 1->3, 3->2, 4->3>
multimap<int, int> mm;

红黑树旋转：

当红黑树性质被破坏的时候，需要调整 → 左旋，右旋。

红黑树的插入或者删除最多旋转树的高度次就可以达到平衡。
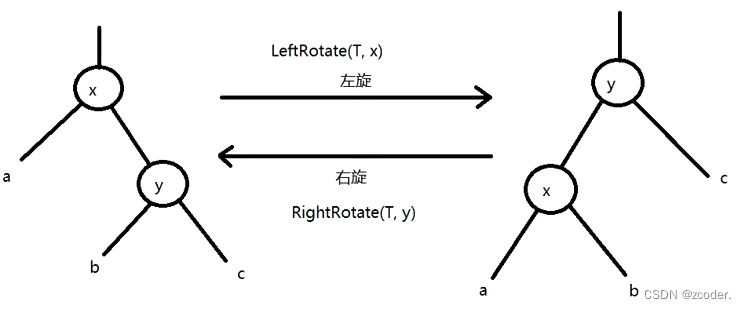
在这里插入图片描述

void rbtree_left_rotate (rbtree *T, rbtree_node *x) {rbtree_node *y = x->right;// 第一步x->right = y->left;if (y->left != T->nil) {y->left->parent = x;}// 第二步y->parent = x->parent;if (x->parent == T->nil){ // x 为根节点T->root = y;} else if (x == x->parent->left) {x->parent->left = y;} else {x->parent->right = y;}// 第三步y->left = x;x->parent = y;
}void rbtree_right_rotate(rbtree *T, rbtree_node *y) {rbtree_node *x = y->left;y->left = x->right;if (x->right != T->nil) {x->right->parent = y;  }x->parent = y->parentl;if (y->parent == T->nil) { // y 为根节点T->root = x;} else if (y == y->parent->right) {y->parent->right= x; } else {y->parent->left= x;}x->right = y;y->parent = x;
}

红黑树插入：
- 红黑树在插入节点以前，它已经是一棵红黑树了。
- 插入节点上色为红色，因为不会改变黑色节点高度。
- 父节点是祖父节点的左子树
  - 叔节点是红色的：
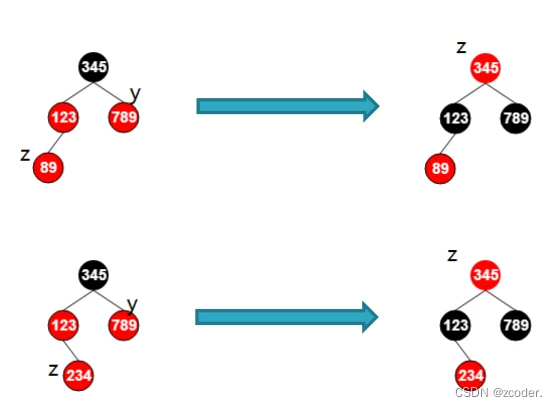
  - 叔节点是黑色的，并且当前节点是右子树。
  - 叔节点是黑色的，并且当前节点是左子树。

七、unordered_map

基于散列表实现了 map。
散列表：
- 将 kv 对 通过对 key 进行 hash 运算映射到一个散列表中的具体位置。
- hash 碰撞：将多个不同的 key 映射到散列表中同一个位置的行为。解决方案有线性探查、拉链法（STL 采用的方法） 等。
- 拉链法：
  - hash 函数依然用于计算数组下标。
  - 数组的每个位置存储一个了链表的表头指针。
  - 每个链表保存具有相同 hash 值的数据。
- 负载因子 = 实际存储的元素个数 $/$ 散列表中桶的个数。
- 当负载因子大于 1 的时候，将发起 rehash。
  - 创建一个更大的桶数组，通常是原来大小的两倍。
  - 散列表中的每个元素根据新的桶数组大小重新计算其 hash 值。在 unordered_map 中，不会重新经过 hash 函数计算，而是将 cache 中的 hash 值对新的桶数组大小取余。
  - 元素根据新的 hash 值被重新插入到新的桶中。
STL 中散列表的实现（使用的单链表，而不是每个桶都指向一个链表）：
- 数据定义：
  - _M_buckets：指针数组。每一个桶都指向该层节点的上一个节点 → 实现头插法。
  - _M_bucket_count：数组长度。
  - _M_element_count：实际存储元素的个数。
  - _M_before_begin：头节点。
  - _M_rehash_policy：rehash 的策略对象。
- 节点定义：
  - 头节点和桶不需要 _M_storage，其他节点需要。
```
struct _Hash_node_value_base : _Hash_node_base {_M_storage;
}
```
- 主要接口：
  - _M_insert_bucket_begin。
```
_M_insert_bucket_begin(size_type __bkt, __node_type* __node) {if (_M_buckets[__bkt]) {__node->_M_nxt = _M_buckets[__bkt]->_M_nxt;_M_buckets[__bkt]->_M_nxt = __node;}else {__node->_M_nxt = _M_before_begin._M_nxt;_M_before_begin._M_nxt = __node;if (__node->_M_nxt)_M_buckets[_M_bucket_index(__node->_M_next())] = __node;_M_buckets[__bkt] = &_M_before_begin;}
}
```
unordered_map 实现：
- typedef __umap_hashtable<_Key, _Tp, _Hash, _Pred, _Alloc> _Hashtable;
- insert 实际调用的是 _M_insert_bucket_begin。
- 无序的结构，搜索的时间复杂度为 $O (1)$ 。

八、迭代器底层实现原理、有哪些种类

提供一种访问容器内元素而不会暴露容器内部实现的方式。
主要作用：
- 解引用（*、->）和成员访问。
- 统一不同容器的访问方式，粘合容器和算法。（STL 提供了容器、算法、迭代器、内存分配器等）
  - find。
  - min_element。
  - upper_bound。
  - reverse。
  - sort。

底层原理：

考虑哪些问题：
- 不是面向对象思想编程，而泛型思想编程。
- 通用算法问题：
  - 迭代器类型：
    - typename 类型别名。
    - 指针类型怎么办 ?
  - 指针类型不能定义类型别名。
  - 怎么根据迭代器类型实现算法。
定义了 5 种类型的迭代器：输入迭代器、输出迭代器、前向迭代器、双向迭代器、随机访问迭代器。
迭代器的关系：

泛型编程中使用了萃取技术，把迭代器内部的各个类型萃取出来。

萃取迭代器用来生成模板，具体的迭代器需要按照这个模板来生成。

template<typename _Category, typename _Tp, typename _Distance = ptrdiff_t,typename _Pointer = _Tp*, typename _Reference = _Tp&>
struct iterator {// 具体的迭代器类型typedef _Category  iterator_category;// 迭代器所指向的元素的类型typedef _Tp        value_type;// 两个迭代器之间的距离typedef _Distance  difference_type;// 指向迭代器所指向元素的指针类型// 如果迭代器指向 int，pointer 将是 int*typedef _Pointer   pointer;// 引用类型，指向迭代器所指向的元素// 如果 value_type 是 int，reference 将是 int&typedef _Reference reference;
};

但是指针类型不能定义别名，所以就需要进行泛型特化，如果出现指针类型，就不使用别名了，直接指定为随机访问迭代器。

template<typename _Tp>
struct iterator_traits<_Tp*> {typedef random_access_iterator_tag iterator_category;typedef _Tp                         value_type;typedef ptrdiff_t                   difference_type;typedef _Tp*                        pointer;typedef _Tp&                        reference;
};

通过函数重载的方式，根据迭代器类型来选择不同的算法实现。

迭代器类型属性：
- 输入迭代器：istream_iterator。
  - 只能在一个方向上进行 ++，一个元素一个元素的挪动。
  - 因为迭代器传递过程中，上一个迭代器会失效，所以迭代器不能被保存。
  - 是只读的并且只能读一次。
- 输出迭代器：ostream_iterator。是只写的并且只能写一次，其他同上。
- 前向迭代器：forward_list、unordered_map、unordered_set。
  - 可读可写，并且可以读写多次。
  - 可以被保存。
- 双向迭代器：list、map、set、multimap、multiset。
  - 可读可写，并且可以读写多次。
  - 可以被保存。
  - 可正向遍历和反向遍历。
- 随机访问迭代器：vector、deque。可以 += n。

在这里插入图片描述

九、迭代器失效、连续和非连续存储容器的失效

迭代器提供一种访问容器内元素而不会暴露容器内部实现的方式。
C++11 之前容器类型：
- 序列型：vector、deque、array。
- 关联型：set、map、multiset、multimap。
- 链表型：forward_list、list、unordered_set、unordered_map、unordered_multiset、unordered_multimap。
失效情况：
- 单独删除或插入：首先持有了某个迭代器，然后通过删除或插入修改了容器，导致持有的迭代器失效了。
  - 插入：insert、emplace*、push_back、push_front。
  - 删除：erase、pop_back、pop_front、clear。
- 遍历删除：
  - 序列型容器：it = container.erase(it);
    - 因为元素都存储在连续空间中，所以删除某个元素时，后面的元素都要往前移，那么对应的迭代器也就都失效了，所以就需要返回元素移动后的、新的、有效的迭代器。
  - 关联型容器：
    - 因为元素存储在不连续空间中，所以删除某个元素时，只有该元素的迭代器失效，后面元素的迭代器都不会失效。
    - C++11 之前：container.erase(it++)。
      - erase 返回的是 void。
      - 在 it 失效以前进行 it++。
    - C++11 及以后：it = container.erase(it); 或 container.erase(it++);
  - 链表型容器：it = container.erase(it); 或 container.erase(it++);
```
for (auto it = c.begin();it != c.end();) {if (shouldDelete(it)){ it = c.erase(it); // c.erase(it++); } else {it++;}
}
```
C++11 容器类型：
- 连续存储容器：it = container.erase(it);
- 非连续存储容器：it = container.erase(it); 或 container.erase(it++);

十、STL 容器线程安全性

容器内的实现已经固定，内部没有加锁，不能修改源码加锁。
容器内部实现原理：
- 扩缩容：
  - vector（扩容）。
  - deque（扩缩容）。
    - priority_queue 默认使用 vector 实现，也可以使用 deque。
    - queue 默认使用 deque 实现，也可以使用 list。
    - stack 默认使用 deque 实现，也可以使用 list。
- rehash：
  - unordered_*。
- 节点关系：
  - vector 中插入或删除会引起后面的节点移动。
  - set、map、multiset、multimap 用红黑树实现，插入或删除会引起红黑树重新平衡。
解决方案：
- 加锁：
  - 互斥锁。
  - 读多写少的情况下，可以使用读写锁：C++14 为 shared_timed_mutex、C++ 17 为 shared_mutex。
  - 并发插入优化。
    - 把插入行为转换为修改数据的行为。
    - 提前分配好节点，提前构建好节点之间的关系。
      - vector 使用 resize。
      - 红黑树 4 兄弟、unordered_*，提前拿到所有的 key。在对同一个 key 并发修改的时候，仍然需要加锁，可使用原子操作。
  - 并发插入删除优化：list：使用生产消费者模型，只对 list 的前后进行操作，生产者线程和消费者线程分别加锁。deque 不可以，基于 deque 的其他容器也不可以。
- 不加锁、避免加锁：
  - 提前分配好节点，并将数据分成多份，每个线程只操作专属那份数据。
  - 缺点：可能出现线程操作不均衡的情况。