[NOIP2000 提高组] 方格取数

题目背景

NOIP 2000 提高组 T4

题目描述

设有 $N\times N$ 的方格图 $(N\le 9)$，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 $0$。如下图所示（见样例）:

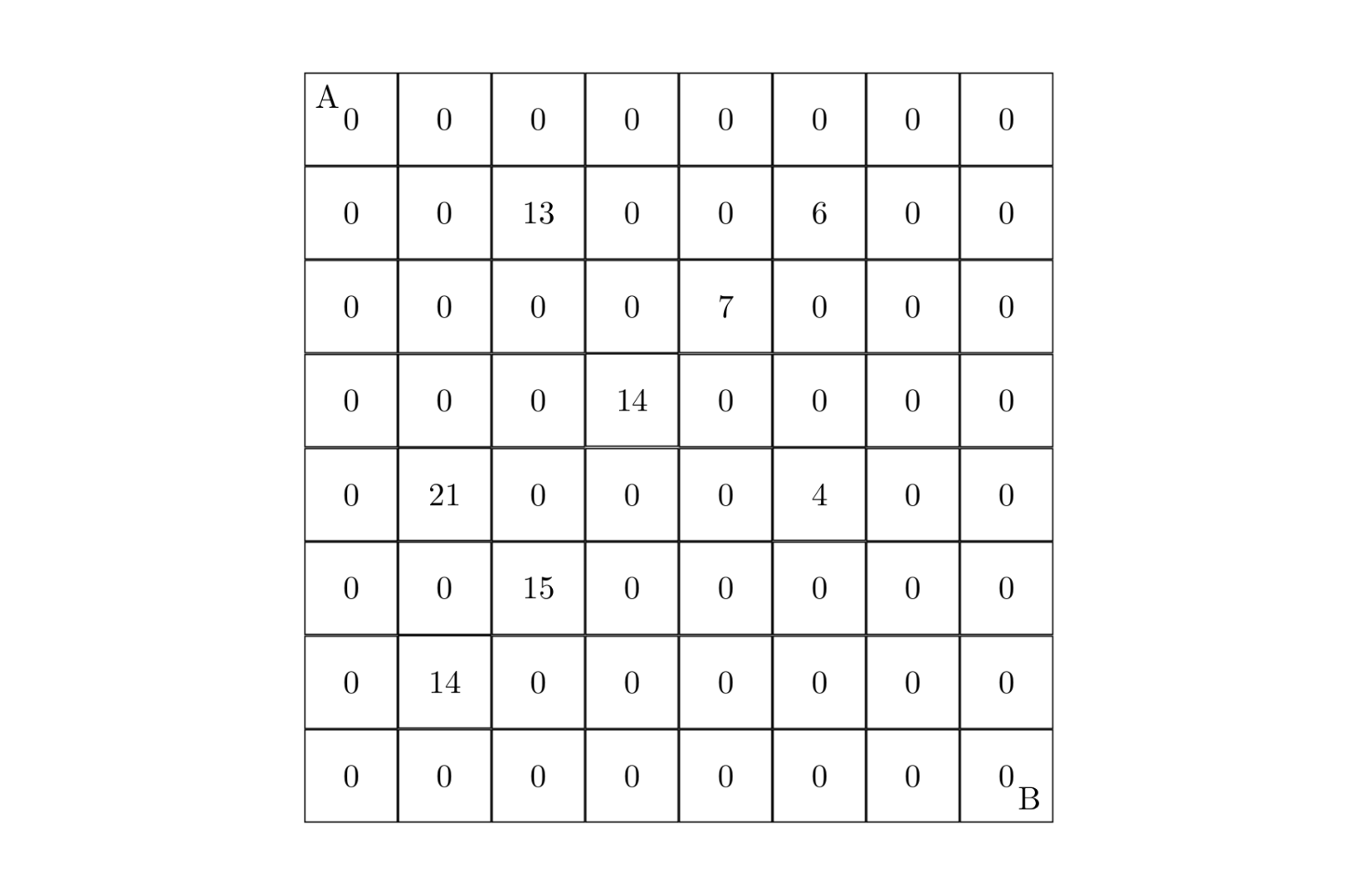
某人从图的左上角的 $A$ 点出发，可以向下行走，也可以向右走，直到到达右下角的 $B$ 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 $0$）。
此人从 $A$ 点到 $B$ 点共走两次，试找出 $2$ 条这样的路径，使得取得的数之和为最大。

输入格式

输入的第一行为一个整数 $N$（表示 $N\times N$ 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 $0$ 表示输入结束。

输出格式

只需输出一个整数，表示 $2$ 条路径上取得的最大的和。

样例 #1

样例输入 #1

8
2 3 13
2 6  6
3 5  7
4 4 14
5 2 21
5 6  4
6 3 15
7 2 14
0 0  0

样例输出 #1

67

提示

数据范围：$1\le N\le 9$。

思路：本题考察dp， 根据闫氏dp分析法我们需要考虑状态表示和状态转移，我们可以同时进行两次的路径， 因此他们的步数应该是相同的， 即 步数 k = i1 + j1 = i2 + j2, 我们还可以考虑到只要两者的横坐标不相同两者的纵坐标一定不相同， 反之则以， 因此我们可以只枚举横坐标， 在根据步数k判断纵坐标， 一共走 2 * n步， 因此可以用dp[][][]来代表总步数为k时的两条路径的总和的最大数值，以上部分即为状态表示。接下来我们考虑状态转移， 我们可以知道一共有四种状态转移，从哪边到达每个点的这四种情况为：上上， 左上, 上左， 左左。由此我们能够写出来状态转移方程为：

由此我们即可写代码了：

AC代码：

#include<bits/stdc++.h>using namespace std;typedef long long ll;
typedef pair<int, int>PII;
const int N=3e5+10;
const int MOD=9901;
const int INF=0X3F3F3F3F;
const int dx[]={-1,1,0,0,-1,-1,+1,+1};
const int dy[]={0,0,-1,1,-1,+1,-1,+1};
const int M = 1e6 + 10;int n;
int w[15][15];
int dp[30][15][15];
int main()
{cin >> n;int a, b, c;while(cin >> a >> b >> c, a || b || c) w[a][b] = c;for(int k = 1; k <= n + n; k ++)//总步数{for(int i1 = 1; i1 <= n; i1 ++)//横坐标1{for(int i2 = 1; i2 <= n; i2 ++)//2{int j1 = k - i1, j2 = k - i2;if(j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n){int t = w[i1][j1];if(i1 != i2) t += w[i2][j2];//说明没有重复dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1 - 1][i2 - 1] + t);dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1][i2 - 1] + t);dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1 - 1][i2] + t);dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1][i2] + t);}//两次同时走路的状态转移}}}cout << dp[n + n][n][n] << endl;return 0;
}