🔥 个人主页：空白诗

---

一、引言

递归，这个在编程世界中既神奇又强大的概念，常常让初学者既着迷又困惑。想象一下，一个函数能够自我调用，层层深入，最终解决复杂问题，就像俄罗斯套娃一样，一层套着一层，直到达到最核心的解答。本文将带你一步步走进递归的世界，用JavaScript这把钥匙，解锁递归之门的秘密！🚪

---

二、什么是递归？

递归，简单来说，就是一个函数在其定义中直接或间接地调用自身的过程。它通常用于解决那些可以通过分解为相似子问题的问题，比如计算阶乘、遍历树形结构、寻找斐波那契数列等。

---

三、两大基本要素

🏁 基线条件（Base Case）

• 定义: 基线条件是递归过程的停靠点，是递归函数不再调用自身的条件。
• 作用: 确保递归不会无限进行，是递归函数能够最终返回结果的关键。
• 特点: 应该是最简单的情况，可以直接给出答案，无需进一步递归。

🔁 递归条件（Recursive Case）

• 定义: 递归条件描述了如何将原问题分解成较小的子问题，并继续调用自身来解决这些子问题。
• 作用: 实现问题的逐步简化，直至达到基线条件。
• 特点: 每次递归调用都应使问题规模减小，趋近于基线条件。

📃 代码示例：计算斐波那契数列

斐波那契数列是递归的经典案例，其中每个数字是前两个数字的和，序列从0和1开始。

斐波那契数列（Fibonacci sequence）是一个非常著名的数列，在数学上有着悠久的历史和广泛的应用。这个数列以其发现者，意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci）的名字命名。斐波那契数列最初是斐波那契在《算盘书》（Liber Abaci）中以兔子繁殖的问题作为例子引入的，因此有时也被称为“兔子数列”。

斐波那契数列的定义是这样的：数列的前两项通常是1（有些定义中第一项为0，第二项为1），之后的每一项都是前两项之和。用数学表达式表示就是：

按照这个规则，数列的前几项是：

斐波那契数列在自然界和艺术中都能找到其身影，比如植物的分支模式、花瓣排列、动物的生长序列等，都与斐波那契数列紧密相关。此外，它还在计算机科学、密码学、经济学、音乐理论等领域有着重要应用，并且与黄金分割比例（大约为1.61803398875）有着密切的数学联系。斐波那契数列的连续两项之比，随着项数的增加，趋近于黄金比例。

JavaScript实现：

function fibonacci(n) {if (n <= 1) {  // 基线条件：n为0或1时，直接返回nreturn n;} else {  // 递归条件：n的值由前两个斐波那契数相加得到return fibonacci(n - 1) + fibonacci(n - 2);}
}console.log(fibonacci(10)); // 输出: 55

• 当调用fibonacci(10)时，它不满足基线条件，因此进入递归条件。
• fibonacci(10)依赖于fibonacci(9)和fibonacci(8)的结果。
• 这个过程会一直持续，直到递归到fibonacci(0)和fibonacci(1)，这两个是基线条件，直接返回0和1。
• 之后，每个递归层开始回溯，计算出各自的结果，最终fibonacci(10)得出55。

💻 代码示例：计算阶乘

阶乘（Factorial），一个在数学领域内同样举足轻重的概念，承载着深厚的理论意义和广泛的实际应用。阶乘源自乘法原理的延伸，其符号表示为n!，读作“n阶乘”。阶乘的提出，虽不如斐波那契数列那样具有传奇色彩的故事背景，却在数学分析、组合数学、概率论乃至计算机科学中占据着不可替代的地位。

阶乘的定义简洁而直观：对于任何非负整数n，

• 如果n为0，则0! 定义为1，这是阶乘的基础约定，保证了递推关系的一致性。
• 若n为正整数（n > 0），则n! = n × (n-1) × (n-2) × … × 2 × 1。

换言之，阶乘意味着将一个数与其以下的所有正整数相乘，形成一个累积的乘积。例如，

阶乘在数学计算中扮演着多重角色，如计算排列数、组合数时它是核心元素，同时也是多项式展开、级数求和、概率分布等领域不可或缺的工具。在计算机科学中，阶乘算法的实现，尤其是递归方法，常作为教学递归思想的经典案例，同时启发了对算法效率、栈空间管理等深入讨论。

function factorial(n) {// 基本情况：0的阶乘是1if (n === 0) {return 1; // 这就是我们的Base Case} else { // 递归情况：n的阶乘是n乘以n-1的阶乘return n * factorial(n - 1); // 这里调用了自身，是Recursive Case}
}console.log(factorial(5)); // 输出: 120

• 当factorial(5)被调用时，它检查n是否为0（基本情况），不是，则继续执行递归情况，即计算5 * factorial(4)。
• 接着factorial(4)调用自己，变成4 * factorial(3)，以此类推，直到factorial(0)。
• 当到达factorial(0)时，这是基本情况，直接返回1，然后每个之前的调用开始返回其计算结果，最终factorial(5)计算完成，输出120。

---

四、递归的注意事项

递归编程作为算法设计的一项基本技能，其有效运用依赖于对几个核心要素的深刻理解和谨慎操作。以下是递归实践中必须留意的关键点：

1. 栈溢出风险：监控递归深度

问题描述示例：计算一个非常大的数的阶乘时，直接递归可能会导致栈溢出。

原始递归代码（存在栈溢出风险）：

function factorial(n) {if (n === 0) return 1;return n * factorial(n - 1);
}console.log(factorial(10000)); // 可能导致栈溢出

应对措施示例：设置递归深度限制

// 定义一个带有深度限制的阶乘计算函数
function factorialWithDepthLimit(n, depth = 0, maxDepth = 1000) { // 添加最大递归深度限制参数// 检查当前递归深度是否超过了设定的最大深度，如果是，则抛出错误if (depth > maxDepth) throw new Error("递归深度超出限制");// 递归终止条件：如果n等于0，返回1if (n === 0) return 1;// 递归调用：n乘以(n-1)的阶乘结果，并增加递归深度计数return n * factorialWithDepthLimit(n - 1, depth + 1, maxDepth);
}// 尝试计算一个大数的阶乘，并捕获可能抛出的错误
try {console.log(factorialWithDepthLimit(10000)); // 尝试计算10000的阶乘
} catch (e) {// 如果发生错误（例如递归深度超限），打印错误信息console.error(e.message);
}

2. 效率考量：平衡计算资源

问题描述示例：计算斐波那契数列时，直接递归会有大量重复计算。

原始递归代码（效率低）：

function fibonacci(n) {if (n <= 1) return n;return fibonacci(n - 1) + fibonacci(n - 2);
}console.log(fibonacci(30)); // 效率极低

这段代码定义了一个带有深度限制的阶乘计算函数factorialWithDepthLimit，旨在防止因递归调用过深而导致的栈溢出错误。函数接受三个参数：要计算阶乘的数n、当前递归深度depth（默认为0）、以及允许的最大递归深度maxDepth（默认为1000）。通过在递归过程中检查深度是否超过最大值，函数能够提前终止递归并抛出错误，从而保护程序免受栈溢出的影响。最后，通过try-catch结构调用该函数并妥善处理可能发生的错误。

优化策略示例：使用记忆化（缓存）

// 初始化一个Map用于存储已经计算过的斐波那契数，键为n，值为第n项斐波那契数
const memo = new Map();// 定义一个使用记忆化的斐波那契函数
function fibonacciMemo(n) {// 如果之前已经计算过这个值，直接从memo中取出返回，避免重复计算if (memo.has(n)) return memo.get(n);let result;// 递归终止条件if (n <= 1) {result = n;} else {// 递归计算前两项斐波那契数之和result = fibonacciMemo(n - 1) + fibonacciMemo(n - 2);}// 计算完成后，将结果存入memo中，供后续可能的使用memo.set(n, result);return result;
}// 调用优化后的函数计算第30项斐波那契数，由于使用了记忆化技术，即使n较大也能高效计算
console.log(fibonacciMemo(30)); // 高效计算

这段代码通过引入一个memo（记忆）对象来存储已经计算过的斐波那契数，确保对于每一个n值，函数只会被调用一次，之后再次请求该值时直接从memo中查找而非重新计算，从而大大提高了计算效率，尤其是在计算较大的斐波那契数时效果显著。

3. 逻辑清晰性：确保易于理解和维护

挑战说明示例：复杂的递归逻辑如汉诺塔问题可能难于理解。

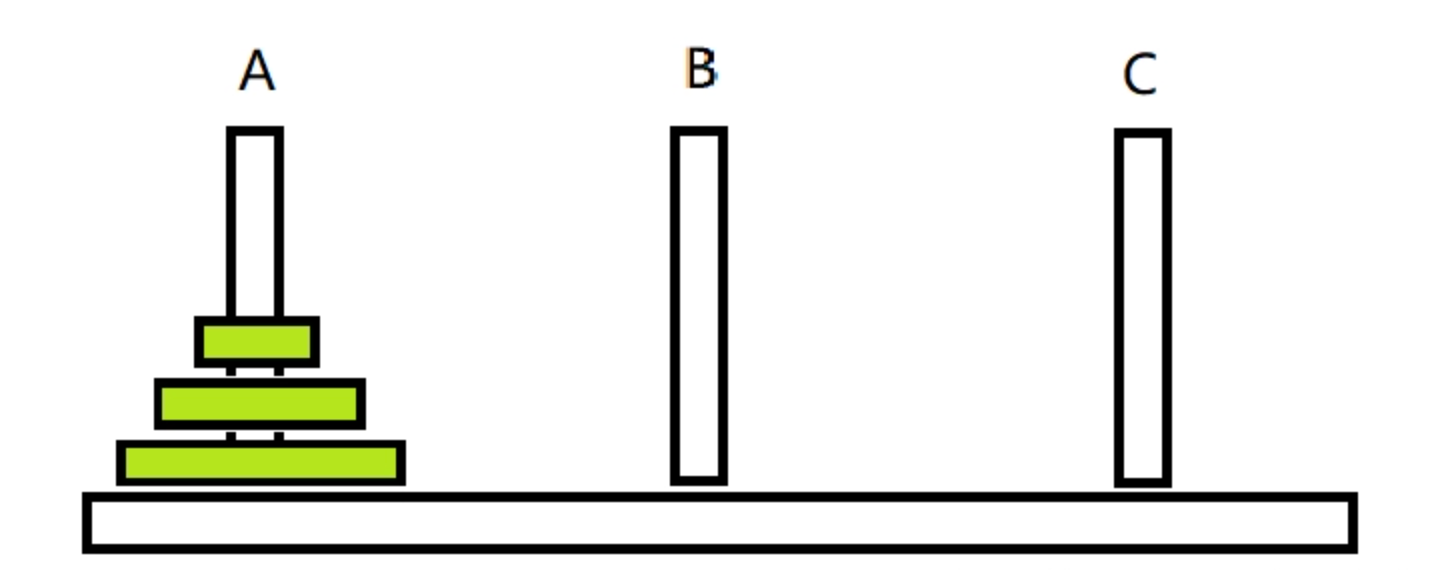
汉诺塔（Tower of Hanoi），又称为河内塔，是一个经典的递归问题和益智游戏，源自印度的一个古老传说。游戏由三根杆子（通常称为A、B、C）和一系列不同大小的盘子组成，最初所有盘子按照从大到小的顺序依次叠放在第一根杆子（A杆）上，且任何时候大盘子都不能放在小盘子之上。

游戏的目标是将所有盘子从起始杆（A杆）移动到目标杆（C杆），并且遵循以下规则：

1. 每次只能移动一个盘子。
2. 在任何时候，盘子都必须保持大盘在下，小盘在上的顺序。
3. 只能通过借助第三根杆子（B杆，作为辅助）来完成移动，但最终所有盘子都必须移到C杆上。

汉诺塔问题可以用递归算法来解决，基本思路是将n个盘子的问题分解为两个子问题：先将上面的n-1个盘子借助C杆移动到B杆，然后将最下面的盘子直接移动到C杆，最后将B杆上的n-1个盘子移动到C杆上。这个过程不断地自我重复，直到只剩下一个盘子，直接移动即可。

汉诺塔不仅是一个有趣的智力游戏，也是计算机科学中教授递归思想的经典案例。通过解决汉诺塔问题，可以深入理解递归算法的设计和分析，以及递归如何通过将复杂问题分解为更简单实例来实现问题的解决。

原始递归代码（稍显复杂）：

function hanoiTower(n, fromRod, toRod, auxRod) {if (n === 1) {console.log(`Move disk 1 from rod ${fromRod} to rod ${toRod}`);} else {hanoiTower(n - 1, fromRod, auxRod, toRod);console.log(`Move disk ${n} from rod ${fromRod} to rod ${toRod}`);hanoiTower(n - 1, auxRod, toRod, fromRod);}
}hanoiTower(3, 'A', 'C', 'B');

解决办法示例：通过清晰的注释和模块化

/*** 使用auxRod作为辅助，将n个盘子从fromRod移动到toRod。* @param {number} n 碟子的数量* @param {string} fromRod 起始柱子* @param {string} toRod 目标柱子* @param {string} auxRod 辅助柱子*/
function hanoiTower(n, fromRod, toRod, auxRod) {// 递归终止条件：如果只有一个盘子，直接从起始柱子移动到目标柱子if (n === 1) {console.log(`将磁盘1从杆${fromRod}移到杆${toRod}`);} else {// 将n-1个盘子从起始柱子借助目标柱子移动到辅助柱子hanoiTower(n - 1, fromRod, auxRod, toRod);// 移动最底下的第n个盘子（此时它是起始柱子上最大的盘子）到目标柱子console.log(`将磁盘${n}从杆${fromRod}移到杆${toRod}`);// 最后，将n-1个盘子从辅助柱子移动到目标柱子hanoiTower(n - 1, auxRod, toRod, fromRod);}
}// 示例：使用清晰的注释和结构化调用来解决3个盘子的汉诺塔问题
hanoiTower(3, 'A', 'C', 'B'); // A为起始柱，C为目标柱，B为辅助柱

这段代码通过递归调用自身来逐步解决问题，展现了汉诺塔问题的分治策略。首先处理较小规模的问题（即将n-1个盘子借助某一柱子移动），然后处理当前规模的特殊部分（即移动最底下的一个盘子），最后再解决剩余的较小规模问题（将n-1个盘子从辅助柱移动到目标柱）。这样的递归逻辑清晰地反映了汉诺塔问题的解决步骤，易于理解和教学。

---

五、递归的好处

为了全面展示递归与传统循环（这里以for和while为例）的区别，我们通过计算斐波那契数列和阶乘两个经典问题来对比递归与循环实现方式。

1. 计算斐波那契数列（While循环实现）

在上文中递归实现直接体现了斐波那契数列的定义，代码简洁。但存在重复计算和高时间复杂度的问题，对于大数容易造成栈溢出。

function fibonacciIterative(n) {let a = 0, b = 1, temp;while (n-- > 0) {temp = a;a = b;b = temp + b;}return a;
}console.log(fibonacciIterative(10)); // 同样输出第10个斐波那契数

循环实现避免了递归的栈溢出风险，性能更高，特别是对于大数计算更为稳定，但可能不如递归直观。

2. 计算阶乘（While循环实现）

在上文中递归直接体现了阶乘的数学定义，代码易于理解，但对于极大数同样面临栈溢出的风险。

function factorialIterative(n) {let result = 1;while (n > 1) {result *= n;n--;}return result;
}console.log(factorialIterative(5)); // 同样输出5的阶乘

而循环实现避免了递归可能导致的栈溢出问题，对于任何大小的输入都能稳定运行，但相比递归可能在表达问题本质方面显得不够直接。

递归的优点在于代码的简洁性和逻辑的直观性，它自然地符合某些问题的结构，比如树形结构遍历或分治算法。而循环，尤其是while循环，提供了更直接的控制流，对于性能敏感或深度大的情况更适用，能够避免递归带来的栈溢出问题。选择哪种方式取决于具体问题、性能要求以及对代码可读性的考量。

综上所述，递归编程是一把双刃剑，既能优雅地解决诸多问题，也暗含着潜在的挑战。通过合理设计、适时优化和清晰的编码实践，我们可以最大化递归的优势，同时有效规避其带来的风险。

---

六、总结

递归与循环（包括for循环和while循环）都是编程中实现重复逻辑的重要手段，它们各自有独特的应用场景和优缺点。通过对比斐波那契数列和阶乘问题的递归与循环实现，我们可以总结如下：

递归的优势:

• 代码简洁: 递归能够以非常直观的方式直接反映问题的数学定义或逻辑结构，使得代码易于理解。
• 自然表达复杂关系: 对于树形结构遍历、分治算法等问题，递归提供了一种自然且优雅的解决方案。
• 逻辑清晰: 递归强调问题分解，将复杂任务分解为更小的相似子问题，有助于理解和设计算法。

递归的劣势:

• 性能问题: 未优化的递归可能导致大量的重复计算和较高的时间复杂度。
• 栈溢出风险: 深度过大的递归调用会消耗过多的调用栈空间，可能引起栈溢出错误。
• 资源消耗: 相较于循环，递归可能消耗更多的内存资源。

循环（特别是while循环）的优势:

• 性能高效: 循环通常提供更好的性能表现，尤其是在处理大量数据或深度循环时，因为它们不涉及额外的函数调用开销。
• 控制灵活: 循环结构提供了更细粒度的控制能力，可以直接管理迭代变量和终止条件。
• 栈空间友好: 不会导致栈溢出问题，适用于需要处理大规模数据或深度迭代的场景。

循环的劣势:

• 逻辑复杂: 对于某些自然递归的问题，使用循环实现可能使得代码逻辑较为繁琐，不易于直观理解。

综上所述，选择递归还是循环应基于具体问题的需求、性能考量、代码可读性以及潜在的规模限制。在追求代码简洁和直观性时倾向于递归，在考虑效率和处理大规模数据时则可能更适合使用循环。此外，实际应用中，也可以结合两者优点，如在递归中引入记忆化技术优化性能，或者利用循环结构模拟递归逻辑，达到最佳的解决方案。

---