Deep Oscillatory Neural Network
公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)


目录
0. 摘要
1. 简介
2. 方法
2.1 深度振荡神经网络(DONN)
2.2 振荡卷积神经网络(OCNN)
2.3 使用振荡神经网络进行分类
3. 实验
F. 动作识别:UCF 11
G. 视频帧预测任务
0. 摘要
我们提出了一种新颖的、受大脑启发的深度神经网络模型,称为深度振荡神经网络(Deep Oscillatory Neural Network,DONN)。像 RNN 这样的深度神经网络确实具有序列处理能力,但网络的内部状态并未设计成展现类似大脑振荡活动的形式。出于这个动机,DONN 被设计成具有振荡内部动态。DONN 的神经元要么是非线性神经振荡器,要么是具有 Sigmoid 或 ReLU 激活的传统神经元。模型中使用的神经振荡器是 Hopf 振荡器,在复数域中描述其动态。输入可以以三种可能的模式呈现给神经振荡器。Sigmoid 和 ReLU 神经元也使用复值扩展。所有的加权阶段也是复值的。训练遵循通过最小化输出误差来改变权重的一般原则,因此总体上类似于复数反向传播。我们还提出了将 DONN 推广到卷积网络的模型,称为振荡卷积神经网络(Oscillatory Convolutional Neural Network,OCNN)。这两种提出的振荡网络被应用于信号和图像/视频处理中的各种基准问题。提出的模型的性能要么与相同数据集上的已发表结果相当,要么更优越。
1. 简介
大量的研究历史表明,大脑中的振荡活动与认知功能 [20]、正常状态下的大脑状态(例如睡眠和清醒)[21] 以及异常状态(例如麻醉 [22] 和癫痫 [23])有关。这些研究使人们了解到,大脑中的感知、记忆和其他高级认知功能是通过大脑中同步振荡网络来实现的。大脑中的振荡神经活动被认为横跨了 0.05 到 500 Hz 的频率范围 [24]。这个广泛的频率范围已经被划分为大约十几个频率带,在对数尺度上呈线性递进。每个频带都与特定的大脑状态相关联,相邻的带与类似状态相关联。
考虑到振荡在大脑功能中的重要性,任何大规模的大脑功能模型都必须容纳这种振荡大脑活动,并反映出各种大脑频率的经验确定的重要性。神经质量模型(Neural mass models) [25] 已经有效地用于描述中观和宏观水平的大脑动态。在这些模型中,基本单位不是单个神经元,而是神经群,其集体活动由非线性的 “神经” 振荡器描述。流行的低维振荡器模型,如 Hopf 振荡器、Wilson-Cowan 振荡器 [26]、FitzHugh-Nagumo [27] 振荡器和 Kuramoto 振荡器已经用于这些网络。这样的振荡网络已被用来描述通过功能性成像技术如 fMRI、MEG 和高密度 EEG 表达的大脑动态 [28]–[33]。然而,尽管这些振荡网络能够捕捉到大脑动态,但它们无法学习输入-输出行为。此外,在那些振荡网络被用来描述行为的情况下,它们通常限于本质上振荡或有节奏的行为,如运动行为 [34]、节奏性手部动作 [35]、游泳动作 [36] 等。
综上所述,有明显的需要发展深度神经网络,其中隐藏层由振荡神经元模型构成。这些网络必须能够学习任何深度神经网络一样的输入/输出行为。在本文中,我们应对这一挑战,提出了一般类的可训练的深度振荡神经网络。
2. 方法
2.1 深度振荡神经网络(DONN)
我们网络中使用的振荡神经元模型是 Hopf 振荡器。它是一个带有稳定极限回路(stable
limit cycle)的谐振器。经典的 Hopf 振荡器由以下复值微分方程描述:
![]()
其中 ω 是 Hopf 振荡器的固有角频率,I(t) 是振荡器的外部输入。极坐标表示对我们的分析更为明确,如下所示:

![]()
其中 Ω 是振荡器和外部输入的角频率之间的差异。振荡器表现出四种不同的动态行为,其特征参数为 (μ, β1, β2):
- 临界 Hopf 区域(critical Hopf regime) (μ = 0, β1 < 0, β2 = 0)
- 超临界 Hopf 区域(supercritical Hopf regime) (μ > 0, β1 < 0, β2 = 0)
- 双极限回路区域(double limit cycle regime) (μ < 0, β1 > 0, β2 < 0)
我们将注意力限制在临界或超临界区域;有关其他区域的更详细分析,请参阅 [37]。然后方程转化为:

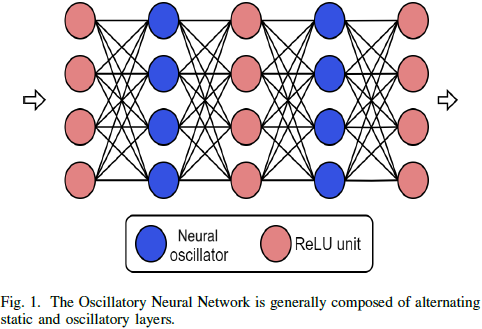

振荡神经网络模型由连续的静态密集或卷积层、非线性激活和动态的 Hopf 振荡器层组成。通用的振荡神经网络如图 1 所示。在正向传播中,输入 z_in(t) 可以以三种模式呈现给振荡器层;要么作为外部输入 I(t),称为谐振器模式,要么作为振幅 μ(t) 的输入,通常称为振幅调制,要么作为频率 ω(t) 的输入,称为频率调制(图 2)。对单个振荡器单元的这三种输入模式的正向传递方法如下描述:
1) 谐振器模式(输入呈现为 I(t)):在外部复值周期驱动(角频率为 ω0)下,z_in(t) = I(t) = I0·e^(i·ω0·t),对于超临界 Hopf 分岔的情况,方程 4 转化为:
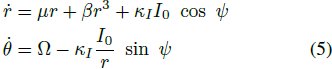
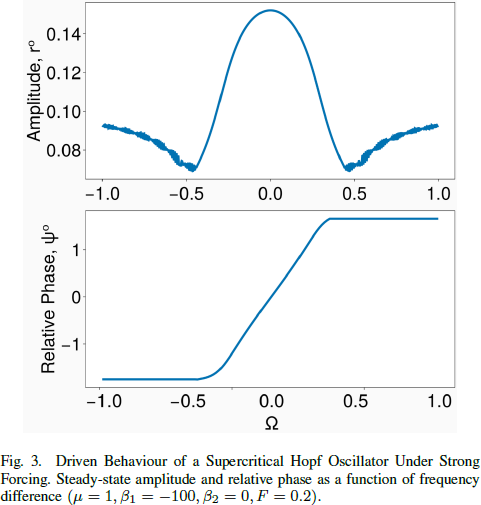
其中 ψ = θ − ω0·t,Ω = ω − ω0 是振荡器和外部输入的角频率之间的差异。在强迫(I0 ≈ 10^-1)的情况下,超临界 Hopf 振荡器的行为如图 3 所示。振荡器在其固有频率附近的一小范围内显示共振。然后,振荡器激活处于与输入信号频率锁定的状态,即振荡器激活的频率等于输入信号的频率。此外,在较小的频率范围内,振荡器激活处于相位锁定状态(图 3)。在此范围之外,系统发生相位滑动。我们注意到,图 3 中描述的共振仅适用于输入具有特定形式的情况,即 I(t) = I0·e^(i·ω0·t)。
2) 振幅调制(输入呈现为 μ(t)):在这种情况下,将 z_in(t) 作为振荡器的 r 方程的输入,动态方程如下:

其中,ℜ 表示复数的实部。由于振荡器的振幅是一个正数,必须确保,κ_μ·min(ℜ(z_in)) + μ0 > 0,其中 min(ℜ(z_in)) 是 ℜ(z_in(t)) 的最小值。
3) 频率调制(输入呈现为 ω(t)):在这种情况下,z_in(t) 被作为振荡器的 θ 方程的输入。在这种情况下,输入调制了有效的振荡器频率,如下所示:
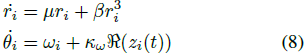
在输入的后两种模式中,Hopf 振荡器的激活受到输入振荡的调制,因此得名。在本文中,我们只使用前两种输入模式来呈现给神经振荡器。上述微分方程从 t = 0 . . . T 使用与数据集相关的固定时间步的前向欧拉方法进行求解。假设上述系统的解为 {r, θ},则输出如下:
![]()
如图 1 所示,将振荡器层的复值激活(方程 9)馈送到静态层中,然后应用复值非线性激活函数 f,如下所示(在时间上逐点):
![]()
其中 ℜ、ℑ 表示复数的实部和虚部。复值非线性激活函数 f 可以是 ReLU、tanh 或 sigmoid 函数。上述所有函数均是连续可微的。我们使用 TensorFlow 库的自动微分功能(autograd)计算反向传播的梯度,以更新网络权重。
2.2 振荡卷积神经网络(OCNN)
在我们提出的 OCNN 模型中,由于存在振荡元素,高层神经元具有时空响应。振荡器的排列与输入特征图相同,以保持空间信息。振荡器的固有频率从适当范围的均匀随机分布中采样。频率分布通过 3x3 的高斯模糊核在每个通道的 2D 振荡器排列上传递。这种卷积和振荡器的层次排列使得在时空尺度上学习和检测不同复杂性水平的特征成为可能,参见图 4。
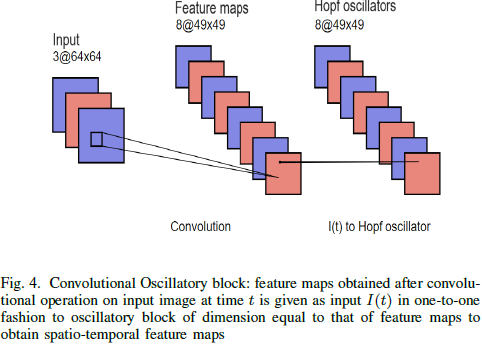
2.3 使用振荡神经网络进行分类
由于 DONN 模型的动态性质,网络的输出始终是一个时间序列。如果网络的任务是一个分类问题,那么标签必须以不同的方式定义。为了对振荡器激活进行等效的分类评分,我们使用阶梯方法来确定预测类别。类似阶梯的分类经常在生物模型中使用,因为它们密切复制了基于竞争的阈值标准来选择获胜神经元 [38]。对于每个时间步,所有类别(最后一层对应的神经元)的期望预测都是零,除了期望的类别,其中期望值线性上升。通过选择在时间步中具有最大平均值的神经元来确定预测类别。
3. 实验
F. 动作识别:UCF 11
为了展示 OCNN 网络在时空领域的序列处理能力,我们使用 UCF11 YouTube 动作数据集 [41] 对网络进行验证。UCF11 是一个标准的 3 通道 RGB 视频分类数据集,具有不同的视角、背景和摄像机运动。该数据集包含 11 个动作类别,所有视频的帧数均设为 50,每帧从原始的 224×224 调整大小为 48×48,考虑到有限的计算能力。数据集被划分为训练集和验证集,分别包含 1290 和 305 个样本。
用于此任务的网络由两对卷积-振荡器层组成,然后是展平(flatten)层和密集(dense)层。用于该任务的网络架构细节如表 VI 所述。振荡器的时间步长设置为 0.02 秒,时间步数等于视频样本中的帧数。Adam(学习率:0.0001)和均方误差(MSE)被用作优化器和损失函数进行训练。

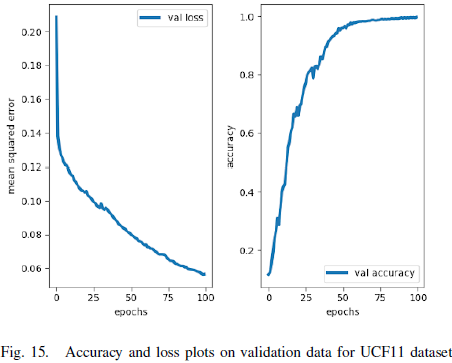
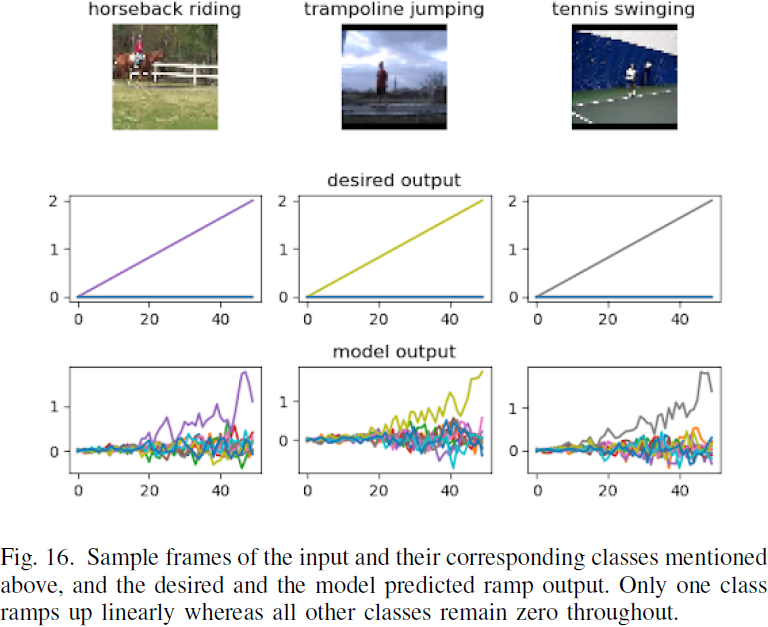
图 15 显示了在验证数据上的准确率和损失曲线,图 16 显示了期望输出和模型输出。该模型的验证 MSE 损失和准确率分别为 0.0564 和 99.75%(p<0.05,n=10)。
G. 视频帧预测任务
在视频帧预测任务中,给定时间 t 的输入帧时,网络必须在时间 t + 1 预测下一个帧 [42]。我们生成了一个合成数据集来进行实验。数据集中的每个视频都是 40×40 的灰度图像,帧数为 16。正方形可以以 360 度中的任一可能方向移动,其中每个正方形的尺寸范围为 2 到 4(图 11)。总共生成了 1000 个这样的视频,使用 8:2 的训练-验证分割。将前 15 帧(t = 0 到 t = 14)作为网络的输入,网络应该预测接下来的 15 帧(t = 1 到 t = 15)。
网络架构如表 VII 所示。使用 Adam 优化器,学习率为 0.001 来优化目标函数,均方误差(MSE)被用作损失函数。总的可训练参数为 30,401。训练后的验证 MSE 损失为 0.04(p<0.05,n=10)。我们模型的一个样本预测如图 17 所示。