🐧主页详情：Choice~的个人主页

搜索旋转排序数组

假设按照升序排序的数组在预先未知的某个点上进行了旋转。

( 例如，数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。

搜索一个给定的目标值，如果数组中存在这个目标值，则返回它的索引，否则返回 -1 。

你可以假设数组中不存在重复的元素。

你的算法时间复杂度必须是 O(log n) 级别。

示例 1:

输入: nums = [4,5,6,7,0,1,2], target = 0
输出: 4

示例 2:

输入: nums = [4,5,6,7,0,1,2], target = 3
输出: -1

方法一 二分查询最大最小值

思路

先算出 数组中最大最小值，利用 indexOf 计算之后要旋转位置，然后二分计算目标 target 位置

详解

1. 计算数组中的最大最小值
2. 定义变量，数组长度等
3. 目标值大于数组最后一位时，数组查询位置从 0 到数字中在最大位置
4. 目标值小于等于数组最后一位时，数组查询位置从数组中最小值的位置开始，到数组的最后一位，3.4 两部为了定位数组查询区间
5. 循环二分查询，计算定位数组的中间值，数组的值等于目标查询结束
6. 不等于的情况，如果目标大于中间值，则定位数组最小值等于中间值+1，目标小于中间值，则定位数组中最大值等于中间值-1，继续循环查询即可，知道定位数组查询完毕，没有结果的话，返回 -1 代表不存在

代码

const search = function (nums, target) {const min = Math.min.apply(null, nums);const max = Math.max.apply(null, nums);const len = nums.length;let pos;let lo;let hi;let mid;if (target > nums[len - 1]) {pos = nums.indexOf(max);lo = 0;hi = pos;} else {pos = nums.indexOf(min);lo = pos;hi = len - 1;}while (lo <= hi) {mid = Math.ceil((lo + hi) / 2);if (nums[mid] === target) return mid;if (nums[mid] < target) {lo = mid + 1;} else {hi = mid - 1;}}return -1;
};

复杂度分析：

• 时间复杂度：O(log(n))O(log(n))

  过程会最多遍历一遍数组

• 空间复杂度：O(1)O(1)

  只产生一次临时变量存储

方法二 二分查询中间数

思路

根据数组的中间数和左右节点的大小对比，来确定升序部分的位置，然后用二分法查询目标节点在数组中的位置

详解

1. 计算数组长度，数组为0 直接返回-1
2. 定义左右值分别为数组第一个和最后一个的下标
3. 中间下标值为最大最小值的平均数
4. 如果数组中间数等于目标直接返回下标
5. 数组的中间值小于数组最后一个值，后半部分还处于升序，如果目标值在这部分数组中，则左下标等于中间值+1，代表目标值在后半部分数组，反着重新定义右下标为中间值-1，目标在前半数组
6. 数组中间值大于数组最后一个值，代表前半部分数组处于升序，如果目标在前半数组中，右标更新为中间值-1，反之，左下标更新为中间值+1
7. 二分查询到最后没找到目标值，则返回 -1 代表不存在

代码

const search = function(nums, target) {if(nums.length === 0){return -1;}let left = 0;let right = nums.length - 1;let mid;while(left <= right){mid = parseInt((left + right) / 2);if(nums[mid] === target){return mid;} else if(nums[mid] < nums[right]) {if(nums[mid] < target && target <= nums[right]) {left = mid + 1;} else {right = mid - 1;}} else {if(nums[left] <= target && target < nums[mid]){right = mid - 1;} else {left = mid + 1;}}}return -1;
};

复杂度分析

• 时间复杂度：O(log(n))O(log(n))

  过程会最多遍历一遍数组

• 空间复杂度：O(1)O(1)

  只产生一次临时变量存储

在排序数组中查找元素的第一个和最后一个位置、数组中的第K个最大元素和颜色分类

在排序数组中查找元素的第一个和最后一个位置

给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。

你的算法时间复杂度必须是 O(log n) 级别。

如果数组中不存在目标值，返回 [-1, -1]。

示例

输入: nums = [5,7,7,8,8,10], target = 8
输出: [3,4]输入: nums = [5,7,7,8,8,10], target = 6
输出: [-1,-1]

方法一 二分查找

思路

由于数组已经时升序排列，可直接根据二分查找，往左定位第一个位置，往右定位最后一个位置 二分查找的实现上可以使用循环或者递归。

详解

1. 根据二分查找，找到左边第一个不小于目标值的位置
2. 从上一步中的位置开始到最后，二分查找，确定右边最后一个符合条件值的位置
3. 得到结果

function getBinarySearchLowerBound (array, low, high, target) {// 找到第一个不小于目标值的位置while (low < high) {const mid = Math.floor((low + high) / 2);if (array[mid] < target) {low = mid + 1;} else {high = mid;}}// 如果相等，则匹配，否则不匹配return array[low] === target ? low : -1;
}function getBinarySearchUpperBound (array, low, high, target) {// 找到第一个不大于目标值的位置while (low < high) {const mid = Math.ceil((low + high) / 2);if (array[mid] > target) {high = mid - 1;} else {low = mid;}}// 如果相等，则匹配，否则不匹配return array[high] === target ? high : -1;
}const searchRange = function (nums, target) {const size = nums.length;const low = getBinarySearchLowerBound(nums, 0, size - 1, target);if (low === -1) {return [-1, -1];}// 从左边数字的位置开始const high = getBinarySearchUpperBound(nums, low >= 0 ? low : 0, size - 1, target);return [low, high];
};

复杂度分析

• 时间复杂度：O(log(n))O(log(n))

  过程中最差情况会遍历二遍数组

• 空间复杂度：O(1)O(1)

  产生三个临时变量存储

数组中的第K个最大元素

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例1：

输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

示例2：

输入: [3,2,3,1,2,4,5,5,6] 和 k = 4
输出: 4

说明：你可以假设 k 总是有效的，且 1 ≤ k ≤ 数组的长度。

方法一

思路

首先通过快速排序的方法将数组升序排序，此时数组的头部为最小的元素，尾部为数组最大的元素。题目要求找到数组中的第 K 个最大的元素，即返回 length - k 个元素即可。

详解

1. 本方法采用快速排序法；
2. 首先通过 arr[Math.floor((start + end) / 2)] 找到数组中间的元素作为主元；
3. 然后使用双指针，分别从数组的头部和尾部遍历数组；
4. 遍历过程中，把比主元小的数都放到主元的左边，比主元大的数都放到主元的右边，实现数组的升序排序；
5. 返回第 length - k 个元素，即为数组中第 k 个最大的元素。

1

const findKthLargest = function (nums, k) {return findK(nums, 0, nums.length - 1, nums.length - k);
};function findK (arr, start, end, k) {if (start === end) return arr[start];// 主元const pivot = arr[Math.floor((start + end) / 2)];let i = start; let j = end;while (i <= j) {while (arr[i] < pivot) i++;while (arr[j] > pivot) j--;if (i <= j) {swap(arr, i, j);i++;j--;}}// 二分查到k位置if (k >= (i - start)) {return findK(arr, i, end, k - i + start);} else {return findK(arr, start, i - 1, k);}
}
// 元素交换
function swap (arr, i, j) {const temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}

复杂度分析

• 时间复杂度： O(n log n)O(nlogn)

上述解法中，采用了快速排序的方法，快排的时间复杂度 O(n log n)O(nlogn)。

• 空间复杂度： O(1)O(1)

上述解法中，申请了四个额外的临时存储空间，这将耗费 O(1)O(1) 的空间。

方法二

思路

首先通过最小堆排序的方法将数组升序排序，排序完的数组如下图所示：

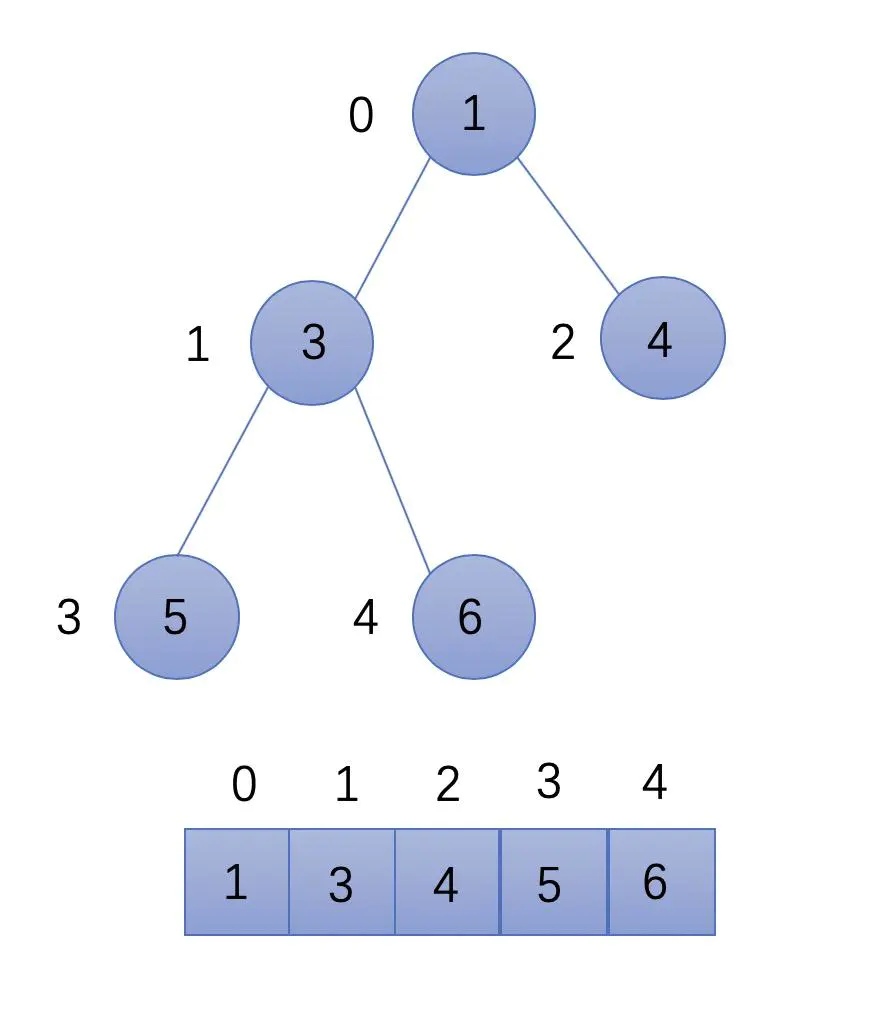
此时数组的头部为最小的元素，尾部为数组最大的元素。题目要求找到数组中的第 K 个最大的元素，即返回 length - k 个元素即可。

详解

1. 本方法采用最小堆排序法；
2. 首先建立最小堆，将每个叶子结点视为一个堆，再将每个叶子结点与其父节点一起构成一个包含更多结点的堆；
3. 所以在构造堆的时候，首先需要找到最后一个结点的父节点，从这个节点开始构造最小堆，直到该节点前面的所有分支节点都处理完毕；
4. 然后返回第 length - k 个，即为数组中第 k 个最大的元素。

const findKthLargest = function (nums, k) {const size = nums.length;// 建立堆for (let i = parseInt(size / 2) + 1; i >= 0; i--) {heapify(nums, i, size);}// 排序for (let j = size - 1; j >= size - k; j--) {// 得到本次的最大，将最大的与最后一个交换位子swap(nums, 0, j);heapify(nums, 0, j);}return nums[size - k];
};function heapify (arr, x, length) {// 左右两个子节点const l = 2 * x + 1;const r = 2 * x + 2;let largest = x;if (l < length && arr[l] > arr[largest]) {largest = l;}if (r < length && arr[r] > arr[largest]) {largest = r;}if (largest !== x) {swap(arr, x, largest);// 递归交换以下的是否也建好堆.heapify(arr, largest, length);}
}function swap (arr, i, j) {const temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}

复杂度分析

• 时间复杂度： O(n log n)O(nlogn)

上述解法中，采用了堆排序的方法，堆排序的时间复杂度 O(n log n)O(nlogn)。

• 空间复杂度： O(1)O(1)

上述解法中，申请了四个额外的临时存储空间，这将耗费 O(1)O(1) 的空间。

方法三

思路

首先通过冒泡排序的方法将数组升序排序，此时数组的头部为最小的元素，尾部为数组最大的元素。题目要求找到数组中的第 K 个最大的元素，即返回 length - k 个元素即可。

详解

1. 本方法采用经典冒泡排序法；
2. 比较相邻的元素，如果第一个比第二个大，就交换他们两个；
3. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对；
4. 完成步骤 3 后，最后的元素会是最大的数，实现升序排序；
5. 返回第 len-k 个元素，即为数组中第 k 个最大的元素。

const findKthLargest = function (nums, k) {const len = nums.length;for (let i = len - 1; i > 0; i--) {// 冒泡排序for (let j = 1; j <= i; j++) {// 异或交换，详见题外话解析if (nums[j - 1] > nums[j]) {nums[j - 1] ^= nums[j];nums[j] ^= nums[j - 1];nums[j - 1] ^= nums[j];}}if (i === (len - k)) {return nums[i];}}return nums[0];
};

复杂度分析

• 时间复杂度： O(n^2)O(n2)

上述解法中，内外两层循环，时间复杂度 O(n^2)O(n2)。

• 空间复杂度： O(1)O(1)

上述解法中，最优的情况是开始时元素已经按顺序排好，空间复杂度为 0 ，最差的情况是开始时元素逆序排序，此时空间复杂度 O(n)O(n)，平均空间复杂度 O(1)O(1)。

复杂度分析：

• 时间复杂度： O(n^2)O(n2)，内外两层循环，时间复杂度 O(n^2)O(n2)
• 空间复杂度： O(1)O(1)，最优的情况是开始时元素已经按顺序排好，空间复杂度为0，最差的情况是开始时元素逆序排序，此时空间复杂度 O(n)O(n)，平均空间复杂度 O(1)O(1)

题外话

对于给定两个整数a,b，下面的异或运算可以实现a,b的交换，而无需借助第3个临时变量：

a = a ^ b;
b = a ^ b;
a = a ^ b;

这个交换两个变量而无需借助第3个临时变量过程，其实现主要是基于异或运算的如下性质：

1. 任意一个变量X与其自身进行异或运算，结果为0，即X ^ X=0
2. 任意一个变量X与0进行异或运算，结果不变，即X ^ 0=X
3. 异或运算具有可结合性，即a ^ b ^ c =（a ^ b）^ c= a ^（ b ^ c）
4. 异或运算具有可交换性，即a ^ b = b ^ a

分析：

第一步： a = a ^ b;

完成后 a变量的结果为a ^ b

第二步： b = a ^ b;

此时赋值号右边的 a 保存的是 a ^ b 的值，那么将赋值号右边的 a 用 a ^ b 替换，

得到（a ^ b） ^ b = a ^ (b ^ b)=a ^ 0=a,

即经过第二步运算后 b 中的值为 a ，即 b=a ，将 a 换到了 b 里

第三步： a = a ^ b;

此时赋值号右边的 a 保存的仍然是 a ^ b 的值，不变，而赋值号右边的 b 已经是 a 了，

将赋值号右边的 a,b 分别进行替换，

即此时赋值号右边 a ^ b=（a ^ b）^ a=a ^ b^ a=a ^ a^ b=0^ b=b, 该值赋值给 a ,即 a=b

即经过第三步运算后 a 中的值为 b ，即 a=b, 将 b 换到了 a 里

这样经过如上的三步骤，完成了交换两个变量 a,b 而无需借助第 3 个临时变量过程。

颜色分类

给定一个包含红色、白色和蓝色，一共 n 个元素的数组，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

此题中，我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

注意: 不能使用代码库中的排序函数来解决这道题。

示例

输入: [2,0,2,1,1,0]
输出: [0,0,1,1,2,2]

方法一 直接计算

思路

直接遍历整个数组，分别计算出红蓝白球的个数，然后按照红色、白色、蓝色顺序依次存入数组。

详解

1. 设定三个变量 red, white，blue 分别表示红球、白球和蓝球。
2. 遍历数组，遇到 0 则使 red 自增1，遇到 1 则使 white 自增1，遇到 2 则使 blue 自增1。
3. 根据红白蓝的个数，依次将 0，1，2 存入数组。

/*** @param {number[]} nums* @return {void} Do not return anything, modify nums in-place instead.*/
const sortColors = function (nums) {let red = 0;let blue = 0;let white = 0;for (let i = 0; i < nums.length; i++) {if (nums[i] === 0) {red++;} else if (nums[i] === 1) {blue++;} else if (nums[i] === 2) {white++;}}let index = 0;for (let i = 0; i < red; i++) {nums[index++] = 0;}for (let i = 0; i < blue; i++) {nums[index++] = 1;}for (let i = 0; i < white; i++) {nums[index++] = 2;}
};

复杂度分析

• 时间复杂度： O(n)O(n)
• 空间复杂度： O(n)O(n)

方法二 双指针遍历

思路

设定三个指针 begin, end, i，用 i 遍历数组，遇到 0，1 时分别将值与 begin, end 指向的值交换。这种方法相对于方法一的好处是只使用了一个常数空间。

详解

1. 设定一头一尾两个指针 begin 和 end，然后用一个指针 i 从头开始遍历数组。
2. 如果遇到 0，则将该数值与begin指向的值交换，并且使begin向后移一位。
3. 如果遇到 2，则将该数值与end指向的值交换，并且使end向前移一位，并且此时不需自加 i。
4. 如果遇到 1，则继续。
5. 最终得到新数组。

/*** @param {number[]} nums* @return {void} Do not return anything, modify nums in-place instead.*/
const sortColors = function (nums) {let begin = 0;let end = nums.length - 1;let i = 0;while (i <= end) {if (nums[i] === 0) {nums[i] = nums[begin];nums[begin] = 0;i++;begin++;} else if (nums[i] === 2) {nums[i] = nums[end];nums[end] = 2;end--;} else {i++;}}
};

复杂度分析

• 时间复杂度：O(n)O(n)
• 空间复杂度：O(1)O(1)

方法三 使用各种排序法

思路

本题的实质是将数字从小到大排序，可以使用各种排序法（冒泡排序法，选择排序法，快速排序法等），这里举一个冒泡排序法的例子。

1

/*** @param {number[]} nums* @return {void} Do not return anything, modify nums in-place instead.*/
const sortColors = function (nums) {for (let i = 0; i < nums.length; i++) {for (let j = 0; j < nums.length - i; j++) {if (nums[j] > nums[j + 1]) {const tem = nums[j];nums[j] = nums[j + 1];nums[j + 1] = tem;}}}
};

复杂度分析

• 时间复杂度：O(n^2)O(n2)

  遍历了两次含n个元素的空间

• 空间复杂度：O(1)O(1)

  排序过程没有用到新的空间存储数据