KAN: Kolmogorov-Arnold Networks

code:https://github.com/KindXiaoming/pykan
Background
多层感知机(MLP)是机器学习中拟合非线性函数的默认模型,在众多深度学习模型中被广泛的应用。但MLP存在很多明显的缺点:
- **参数量大:**Transformer中,MLP几乎消耗了所有非嵌入参数。
- **缺乏可解释性:**在没有后期分析工具的情况下,相较于注意力层通常难以解释。
Novelty
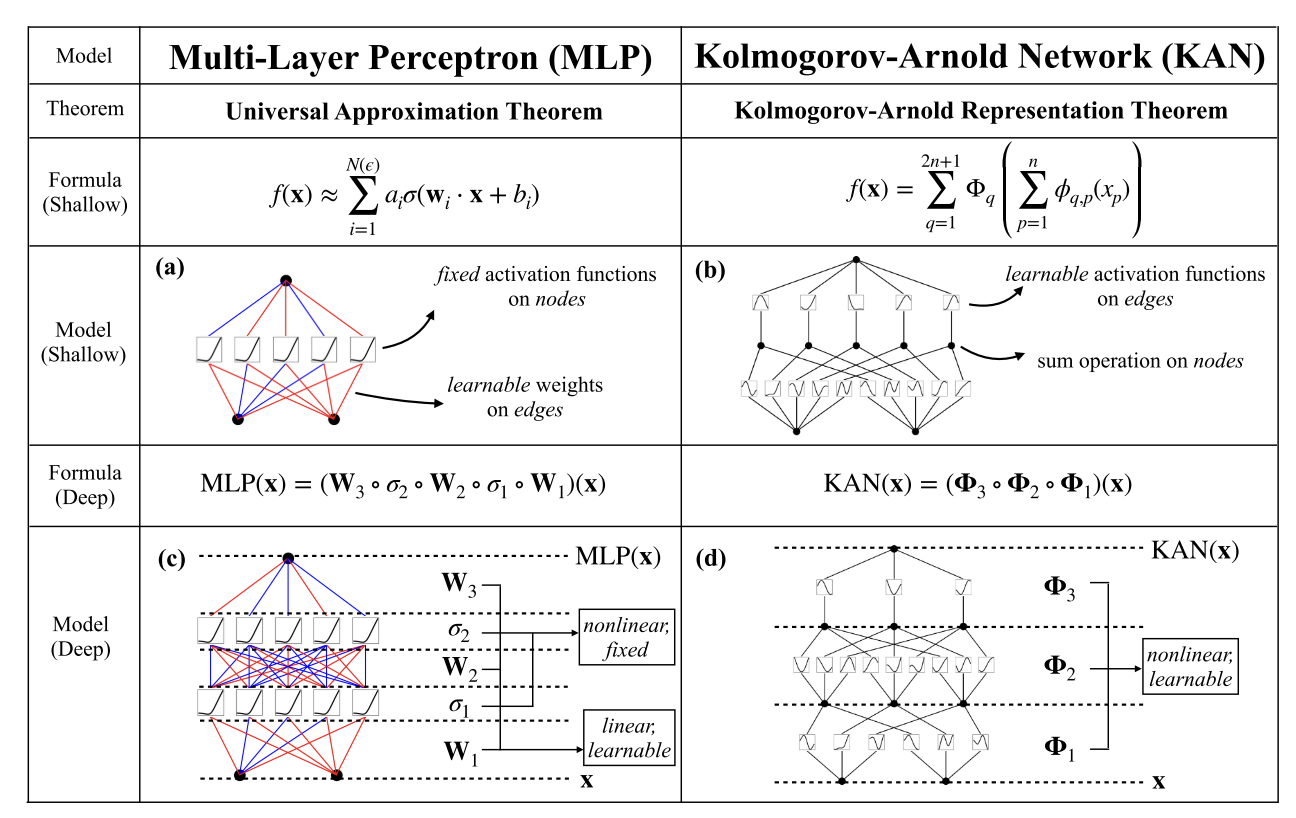
受到Kolmogorov-Arnold 表示定理启发,提出了一种有希望的MLP替代方案,称为Kolmogorov-Arnold Networks(KANs)。
MLP将固定的激活函数放在节点(“神经元”)上,而KAN将可学习的激活函数放在边缘(“权重”)上。
对于PDE求解,2x10 的KAN比4x100 MLP精确100倍(10−7 vs 10−5 MSE),参数效率高100倍( 1 0 2 10^2 102 vs 1 0 4 10^4 104参数)。
Method
Kolmogorov-Arnold表示定理
基本形式:
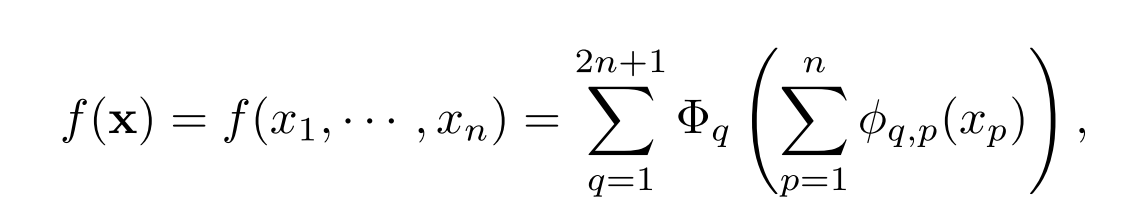
这个公式仅仅包含两层非线性和少量的隐藏层项(2n+1)。这意味着原始的表示方法虽然理论上是完备的,但在处理实际问题时可能因表达能力受限而不够有效。
本文将把网络泛化到任意宽度和深度,可以增加模型的复杂度和学习能力,使得网络能够更好地逼近和表达各种复杂的函数。
KAN结构
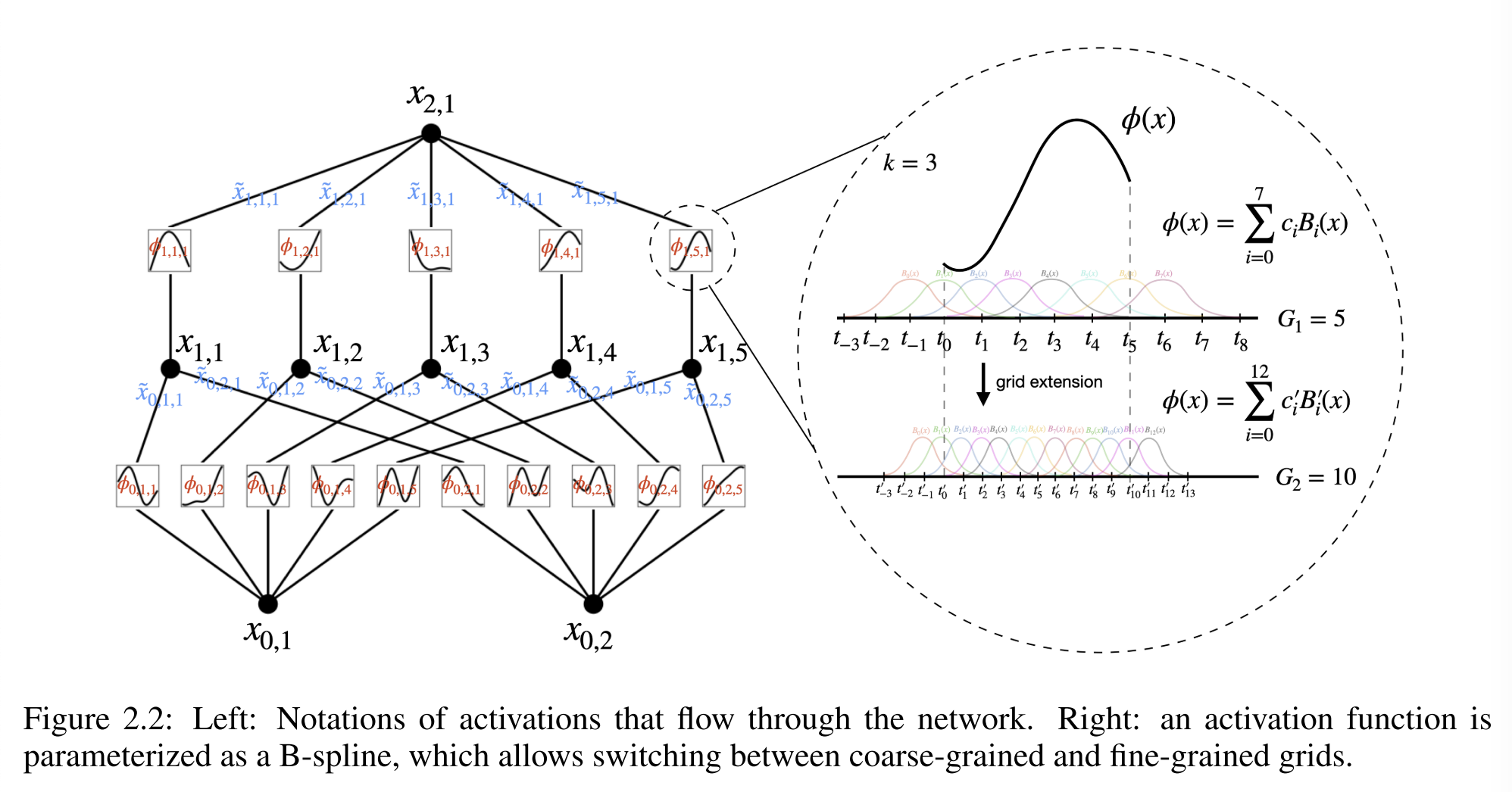
把网络泛化到任意宽度和深度:
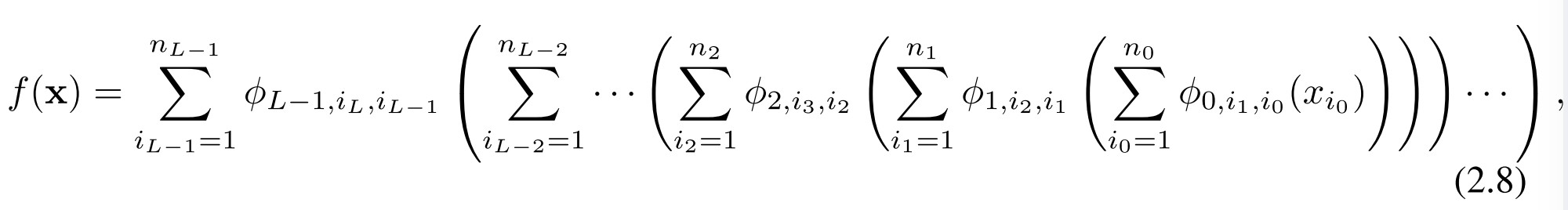
激活函数:

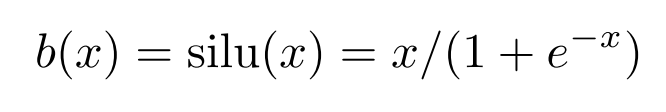
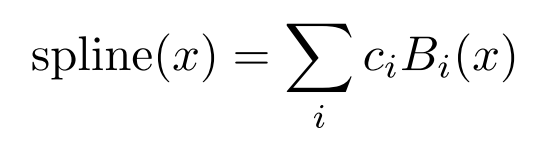
c i c_i ci是可训练的。原则上w是多余的,因为它可以被包括到b(x)和spline(x)中。然而,KAN中仍使用了w,以更好地控制激活函数的总体大小。
初始化:
每个激活函数初始化为 s p l i n e ( x ) ≈ 0 spline(x)≈0 spline(x)≈0。w根据Xavier初始化进行初始化。
网格扩展
增加MLP的宽度和深度可以提高性能,但不同大小的MLP训练是独立的,训练这些模型的成本很高。
KAN可以先用一个参数较少的模型进行训练,然后通过使其样条网格更精细,将其扩展到具有更多参数的KAN,而不需要从头开始重新训练更大的模型。通过以下公式利用最小二乘法来获得细网格的参数:
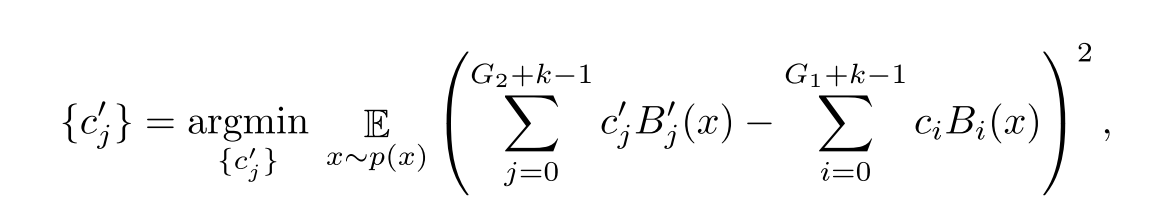
简化KAN
从一个足够大的KAN开始,用稀疏性正则化训练它,然后进行修剪。
稀疏化
在训练MLP时通常使用L1范数来鼓励模型的权重向量中有更多的零,从而达到稀疏化的效果。但L1不足以使KAN稀疏化,需要一个额外的熵正则化。
定义每一个激活函数的L1范数为:
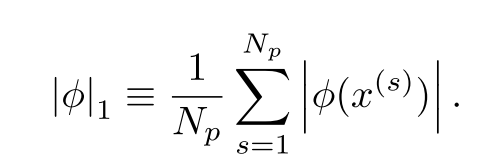
KAN的每一层的L1范数为所有激活函数的L1范数之和:
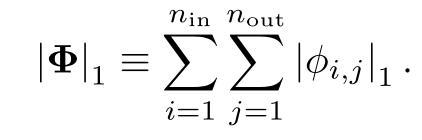
定义KAN的每一层的熵为:
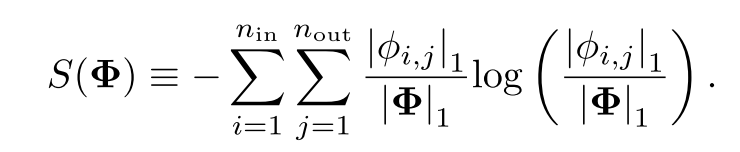
总的训练损失为预测损失与所有KAN层的L1和熵正则化之和:
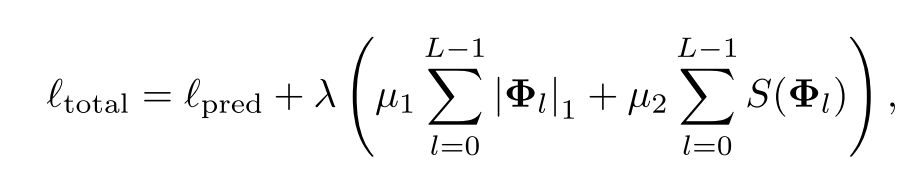
剪枝
对于每个节点来对KAN进行剪枝,定义每个结点的传入和传出分数为:
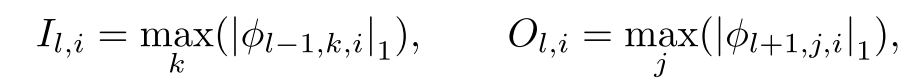
如果传入和传出的分数都小于0.01,则认为该神经元时不重要的,将其修剪。
符号化
一些激活函数实际上是符号函数(如cos、log等),作者提供了一个接口来将他们设置为制定的符号函数f的形式。但激活函数的输出和输出可能有偏移和缩放,因此从样本中获取预激活值x和后激活值y,并拟合仿射函数 y ≈ c f ( a x + b ) + d y≈cf(ax+b)+d y≈cf(ax+b)+d。

人类用户可以通过观察KAN可视化的激活函数,猜出这些符号公式,并将这些激活函数直接设置为该公式,再去拟合仿射函数。通过这样注入人类的归纳偏差或领域知识使得拟合的结果更加精准。
Experiment
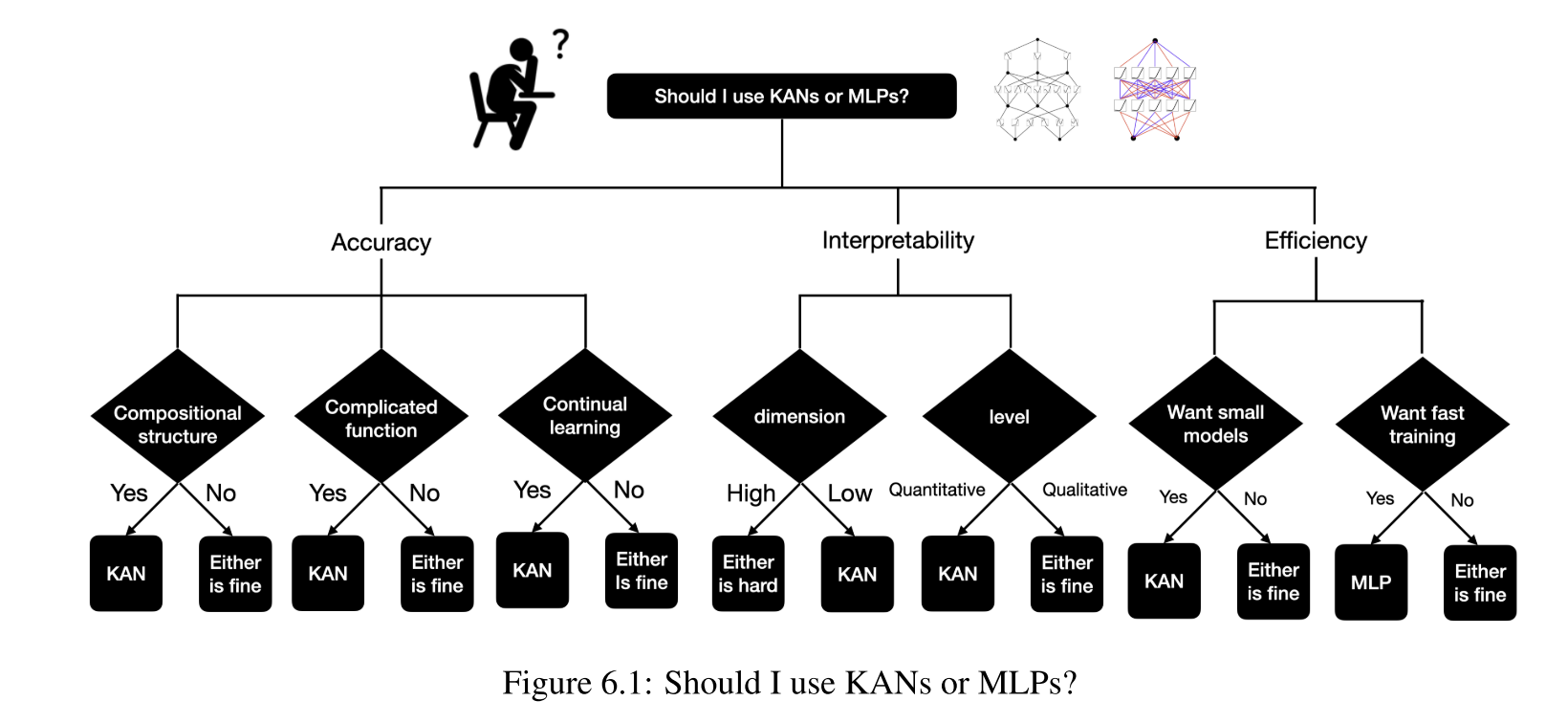
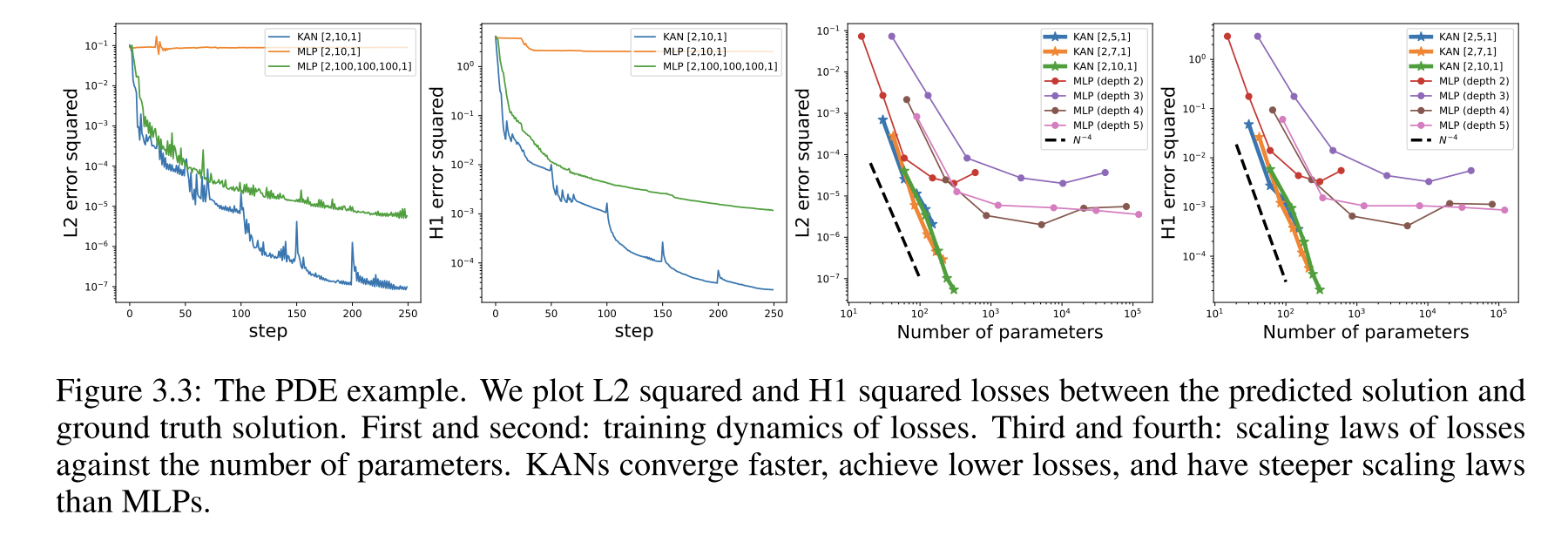
神经标度律(scaling law):KAN比MLP有着更快的标度变化速度。在求解偏微分方程任务中,KANs也展现出更快的收敛速度、达到更低的损失,并有着更陡峭的标度率表现。
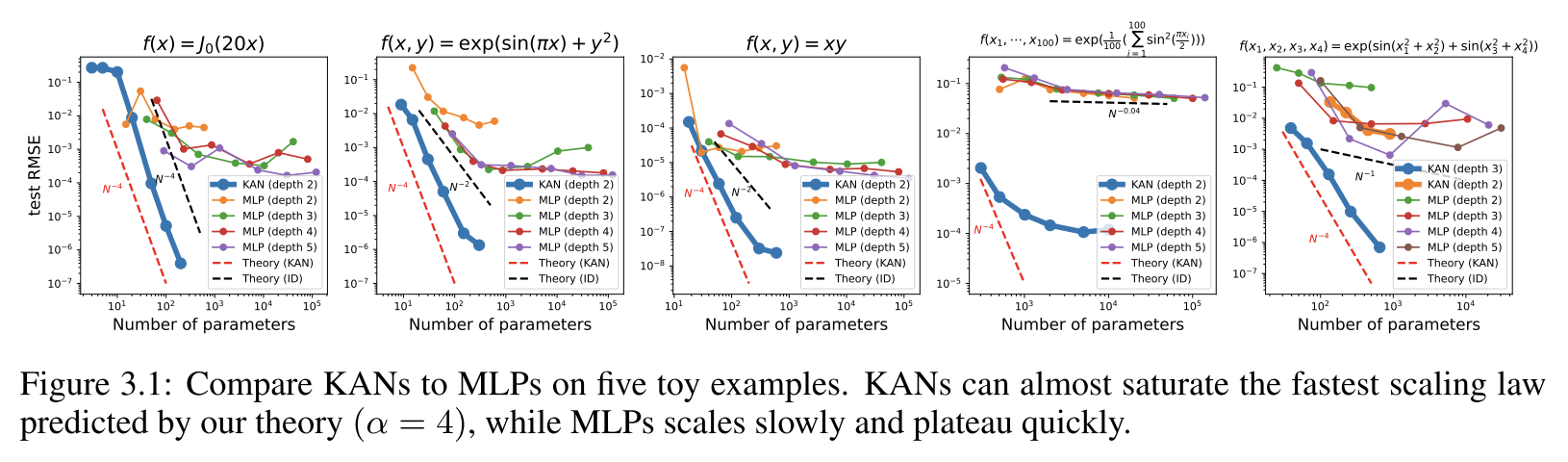
**函数拟合:**KAN比MLP更准确,具有更好的Pareto边界
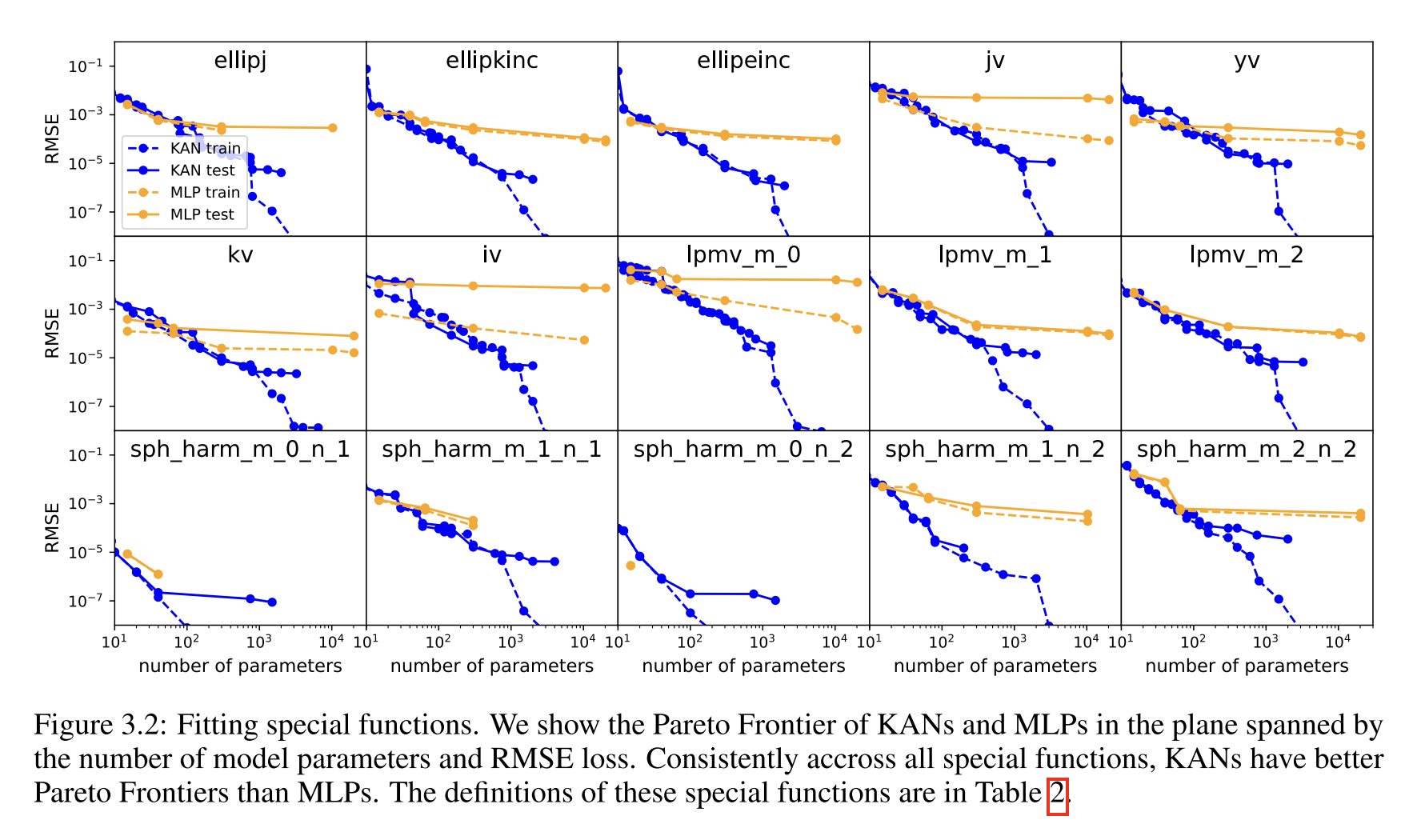
**偏微分方程求解:**在求解泊松方程时,KAN比MLP更准确,敛速度更快,损失更低,并且具有更陡峭的神经标度率表现。
**持续学习:**借助样条设计的局部性天然优势,KAN可以在新数据上实现持续学习,规避了机器学习中存在的灾难性遗忘问题。

**可解释性:**KAN能通过符号公式揭示合成数据集的组成结构和变量依赖性。

人类用户可以与 KANs 交互,使其更具可解释性。在 KAN 中注入人类的归纳偏差或领域知识非常容易。
Limitation
KAN最大的瓶颈在于训练速度慢。在参数数量相同的情况下,KAN通常比MLP慢10倍,这需要在未来加以改善。