【1572. 矩阵对角线元素的和】-编程知识

【1572. 矩阵对角线元素的和】

来源：力扣（LeetCode）

描述：

给你一个正方形矩阵 mat，请你返回矩阵对角线元素的和。

请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。

示例 1：

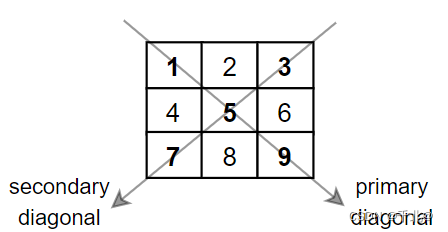
输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：25
解释：对角线的和为：1 + 5 + 9 + 3 + 7 = 25
请注意，元素 mat[1][1] = 5 只会被计算一次。

示例 2：

输入：mat = [[1,1,1,1],[1,1,1,1],[1,1,1,1],[1,1,1,1]]
输出：8

示例 3：

输入：mat = [[5]]
输出：5

提示：

n == mat.length == mat[i].length
1 <= n <= 100
1 <= mat[i][j] <= 100

方法一：遍历矩阵

思路与算法

我们知道矩阵中某个位置 (i, j) 处于对角线上，则一定满足下列条件之一：

i = j；
i + j = n − 1；

根据上述结论，我们可以遍历整个矩阵，如果当前坐标 (i, j) 满足 i = j 或者 i + j = n − 1 则表示该位置一定在对角线上，则把当前的数字加入到答案之中。

代码：

class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size(), sum = 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {if (i == j || i + j == n - 1) {sum += mat[i][j];}}}return sum;}
};

时间 12ms 击败 77.20%使用 C++ 的用户
内存 10.61mb 击败 89.00%使用 C++ 的用户
复杂度分析

时间复杂度：O(n²)，其中 n 是矩阵 mat 的行数。
空间复杂度：O(1)。

方法二：枚举对角线元素

思路与算法

逐行遍历，记当前的行号为 i，则当前行中处于对角线的元素为：坐标 (i, i) 和坐标 (i, n − i − 1)，因此我们把 (i, i) 与 (i, n − i − 1) 处的数字加入到答案中。如果 n 是奇数的话，则主对角线与副对角线存在交点 (⌊ $\over 2$ ⌋, ⌊ $\over 2$ ⌋)，该点会被计算两次。所以当 n 为奇数的时候，需要减掉交点处的值。

代码：

class Solution {
public:int diagonalSum(vector<vector<int>>& mat) {int n = mat.size(), sum = 0, mid = n / 2;for (int i = 0; i < n; ++i) {sum += mat[i][i] + mat[i][n - 1 - i];}return sum - mat[mid][mid] * (n & 1);}
};