文章目录
- 一、优化问题
- (一)数学优化
- (二)凸优化
- 二、凸集
- (一)一些标准凸集
- (二)保留凸性的运算
- (三)正常锥和广义不等式
- (四)分离和支撑超平面
一、优化问题
(一)数学优化
从本质上讲,人工智能的目标就是最优化——在复杂环境中与多体交互中做出最优决策。几乎所有的人工智能问题都会归结为一个优化问题。
- 优化目标:minimize f 0 ( x ) f_0(x) f0(x)
- 约束条件:
- 非等式约束: f i ( x ) ≤ 0 , i = 1 , . . . , m f_i(x)\leq0,i=1,...,m fi(x)≤0,i=1,...,m
- 等式约束: g i ( x ) = 0 , i = 1 , . . . , m g_i(x)=0,i=1,...,m gi(x)=0,i=1,...,m
将最优化问题用于求解最佳决策时, x x x代表决策,约束用于限制决策或对结果施加条件
将最优化问题用于求解最优模型时, x x x 表示模型中的参数,约束对模型参数提出要求(例如,非负性)
最优化问题一般情况下不能得到完全的解决,但是可以尝试近似地解决它,而且通常无伤大雅。这个问题的例外情况是:凸优化问题。
一般非凸问题的传统技术通常会涉及到一定的妥协:
- 局部优化方法(非线性规划)
- 在其附近的可行点中找到一个使 f 0 f_0 f0 最小的点
- 可以处理大问题,例如神经网络训练
- 需要初始猜测,并且通常需要算法参数微调
- 不提供有关找到的点有多次优的信息
- 全局优化方法
- 找到(全局)解决方案
- 最坏情况的复杂性随着问题的规模呈指数级增长
- 通常基于解决凸子问题
(二)凸优化
凸优化问题是特殊形式的优化问题,包括线性规划 (LP)、二次规划 (QP) 等,我们通常能够可靠、高效地解决这些问题。
- 优化目标:minimize f 0 ( x ) f_0(x) f0(x)
- 约束条件:
- 非等式约束: f i ( x ) ≤ 0 , i = 1 , . . . , m f_i(x)\leq0,i=1,...,m fi(x)≤0,i=1,...,m
- 等式约束: A x = b Ax=b Ax=b
凸优化问题与最优化问题的对比:
- 凸优化问题的等式约束是线性的
- f 0 , . . . , f m f_0,..., f_m f0,...,fm是凸的: θ ∈ [ 0 , 1 ] , f i ( θ x + ( 1 − θ ) y ) ≤ θ f i ( x ) + ( 1 − θ ) f i ( y ) \theta \in [0,1],f_i(\theta x+(1-\theta)y)\leq\theta f_i(x)+(1-\theta)f_i(y) θ∈[0,1],fi(θx+(1−θ)y)≤θfi(x)+(1−θ)fi(y)
二、凸集
(一)一些标准凸集
仿射集包含通过集合中任意两个不同点的线(通过 x 1 x_1 x1、 x 2 x_2 x2两点的线: x = θ x 1 + ( 1 − θ ) x 2 , θ ∈ R x=\theta x_1+(1-\theta)x_2,\theta \in R x=θx1+(1−θ)x2,θ∈R)
- 函数形式为f=Ax+b,则称函数是仿射的,即线性函数加常数的形式。
- 比如线性方程组的解 { x ∣ A x = b } \{x |Ax = b\} {x∣Ax=b},并且每个仿射集都可以表示为线性方程组的解集

凸集包含集合中任意两点之间的线段( x 1 x_1 x1和 x 2 x_2 x2两点间的线段: x = θ x 1 + ( 1 − θ ) x 2 , 0 ≤ θ ≤ 1 x=\theta x_1+(1-\theta)x_2,0\leq\theta\leq1 x=θx1+(1−θ)x2,0≤θ≤1)
- 凸集满足对于 x 1 , x 2 ∈ C , 0 ≤ θ ≤ 1 x_1,x_2\in C,0\leq\theta\leq1 x1,x2∈C,0≤θ≤1,有 θ x 1 + ( 1 − θ ) x 2 ∈ C \theta x_1+(1-\theta)x_2\in C θx1+(1−θ)x2∈C;
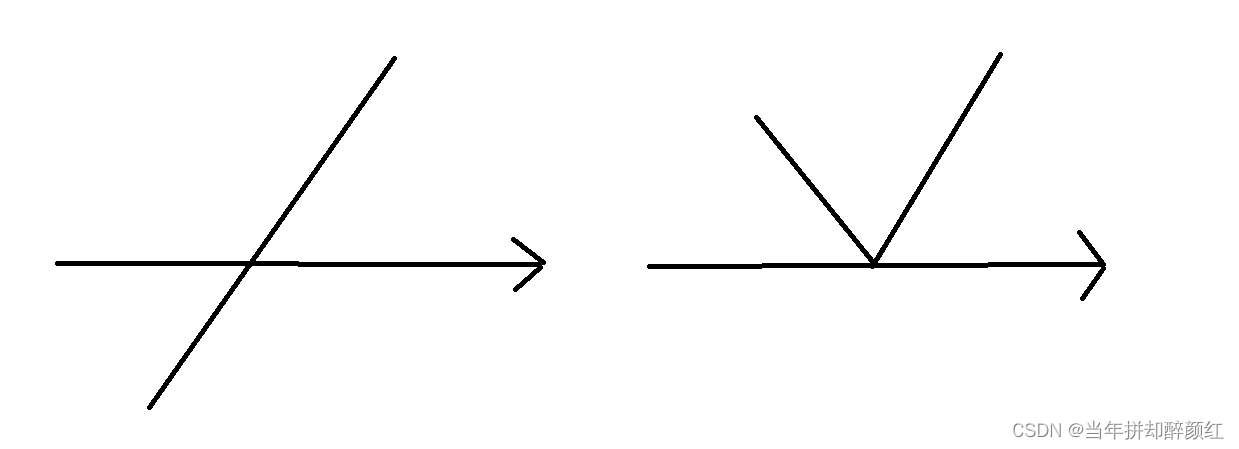
- 以下为一个凸集和两个非凸集的示意:

为什么 x = θ x 1 + ( 1 − θ ) x 2 x=\theta x_1+(1-\theta)x_2 x=θx1+(1−θ)x2可以表示任意两点连接线段的所有点?将上式展开得:
x = θ x 1 + ( 1 − θ ) x 2 = θ x 1 + x 2 − θ x 2 = θ ( x 1 − x 2 ) + x 2 x=\theta x_1+(1-\theta)x_2=\theta x_1+x_2-\theta x_2=\theta(x_1-x_2)+x_2 x=θx1+(1−θ)x2=θx1+x2−θx2=θ(x1−x2)+x2
凸包: S 中所有点的凸组合的集合( x 1 , . . . , x k x_1,...,x_k x1,...,xk的凸组合: x = θ 1 x 1 + θ 2 x 2 + . . . + θ k x k x=\theta_1 x_1+\theta_2 x_2+...+\theta_k x_k x=θ1x1+θ2x2+...+θkxk,其中 θ 1 + . . . + θ k = 1 , θ i ≥ 0 \theta_1+...+\theta_k =1,\theta_i \geq 0 θ1+...+θk=1,θi≥0)

凸锥体: 包含集合中点的所有圆锥组合的集合( x 1 x_1 x1和 x 2 x_2 x2的圆锥组合: x = θ 1 x 1 + θ 2 x 2 x=\theta_1 x_1+\theta_2 x_2 x=θ1x1+θ2x2,且 θ 1 ≥ 0 , θ 2 ≥ 0 \theta_1\geq0,\theta_2\geq0 θ1≥0,θ2≥0)

超平面: 形式为 { x ∣ a T x = b } \{x | a^T x = b\} {x∣aTx=b}的集合,其中 a ≠ 0 a ≠ 0 a=0,半空间: 形式为 { x ∣ a T x ≤ b } \{x | a^T x \leq b\} {x∣aTx≤b}的集合,其中 a ≠ 0 a ≠ 0 a=0。(a是法向量,超平面是仿射和凸的;半空间是凸的)

欧几里得球: B ( x c , r ) = { x ∣ ∣ ∣ x − x c ∣ ∣ 2 ≤ r } = { x c + r u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } B(x_c,r)=\{x|\ ||x-x_c||_2\leq r\} = \{x_c+ru|\ ||u||_2\leq1\} B(xc,r)={x∣ ∣∣x−xc∣∣2≤r}={xc+ru∣ ∣∣u∣∣2≤1}
椭球: { x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } = { x c + r u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } = { x c + A u ∣ ∣ ∣ u ∣ ∣ 2 ≤ 1 } \{x|\ (x-x_c)^T P^{-1}(x-x_c)\leq 1\} = \{x_c+ru|\ ||u||_2\leq1\} = \{x_c+Au|\ ||u||_2\leq1\} {x∣ (x−xc)TP−1(x−xc)≤1}={xc+ru∣ ∣∣u∣∣2≤1}={xc+Au∣ ∣∣u∣∣2≤1},其中 P ∈ S + + n P\in S^n_{++} P∈S++n,也就是说P 对称正定,A平方且非奇异。
中心为 x c x_c xc,半径为 r r r 的标准球: { x ∣ ∣ ∣ x − x c ∣ ∣ ≤ r } \{x|\ ||x − x_c|| ≤ r\} {x∣ ∣∣x−xc∣∣≤r}
标准锥: { ( x , t ) ∣ ∣ ∣ x ∣ ∣ ≤ t } \{(x, t) |\ ||x||≤t\} {(x,t)∣ ∣∣x∣∣≤t}
欧几里得范数锥: { ( x , t ) ∣ ∣ ∣ x ∣ ∣ 2 ≤ t } \{(x, t) |\ ||x||_2≤t\} {(x,t)∣ ∣∣x∣∣2≤t}
多面体 是有限多个线性不等式和等式的解集,也是有限数量的半空间和超平面的交集。 { x ∣ A x ≤ b , C x = d } \{x| Ax\leq b,Cx=d\} {x∣Ax≤b,Cx=d}
(二)保留凸性的运算
证明集合 C 凸性的方法:
- 基于定义:如果 x 1 , x 2 ∈ C , 0 ≤ θ ≤ 1 x_1,x_2\in C,0\leq\theta\leq 1 x1,x2∈C,0≤θ≤1,则有 θ x 1 + ( 1 − θ ) x 2 ∈ C \theta x_1+(1-\theta)x_2\in C θx1+(1−θ)x2∈C;
- 使用凸函数;
- 表明 C 是通过保留凸性的操作从简单凸集(超平面、半空间、范数球……)获得的;
交运算:(任意数量的)凸集的交集是凸的。

仿射映射:凸集的仿射映射也是凸的。(函数形式为f=Ax+b,则称函数是仿射的,即线性函数加常数的形式。)
 (仿射变换就认为是一个矩阵变换,足球可以映射成一个橄榄球,依然是凸集。)
(仿射变换就认为是一个矩阵变换,足球可以映射成一个橄榄球,依然是凸集。)
由仿射变换推出凸集的和也是凸集:

透视函数:凸集在透视下的像和逆像都是凸的(透视函数实际上就是对向量进行伸缩规范化)

线性分数函数是仿射映射函数和透视变换的复合函数,依然还是保凸运算,凸集在线性分数函数下的像和逆像都是凸的。从联合概率到条件概率的变换是一个线性分数函数。

(三)正常锥和广义不等式
正常锥的定义:如果凸锥体 K ⊆ R n K⊆R_n K⊆Rn满足如下条件,则称锥 K ⊆ R n K⊆R_n K⊆Rn为正常锥。
- K是凸的
- K是闭的
- K是实的,即K有非空的内部
- K是尖的,即K不包含任何直线

广义不等式满足类似普通不等式的性质,如传递性,反对称性等等。 广义不等式和普通不等式最大的区别是不是任意两点都是可比的。即 x ≤ y x≤y x≤y 和 y ≤ x y≤x y≤x对于普通不等式二者必居其一。而对于广义不等式这不一定成立。所以最小,最大这些概念对于广义不等式变得很复杂。
(四)分离和支撑超平面
分离超平面:利用超平面将两个不相交的凸集分离开来,即得到超平面分离定理。


支撑超平面:如果C是凸的,那么在C的每个边界点都存在一个支持超平面。

 支撑超平面不完全逆定理:如果一个集合是闭的,具有非空内部并且其边界上每个点均存在支撑超平面,那么它是凸的。
支撑超平面不完全逆定理:如果一个集合是闭的,具有非空内部并且其边界上每个点均存在支撑超平面,那么它是凸的。
参考:
凸优化之保凸运算
广义不等式
【最优化理论与算法】数学预备知识、凸集和凸函数