摘要:什么是搜索二叉树,实现搜索二叉树(及递归版本)
什么是搜索二叉树
搜索二叉树/二叉排序树/二叉查找树·BST(Binary Search Tree):特征——左小右大(不允许重复值)。即取搜索二叉树中任一结点为根往下看,总满足左子树所有结点的值都小于根的值,右子树所有结点的值都大于根结点的值。
搜索二叉树图例如下:

实现搜索二叉树
(不需要 namespace 封装,因为这不是模拟实现,不会和库里产生冲突)
1. 创建结点_Node
class K 的这个 K 是搜索二叉树的一个命名惯例(Convention),即 key(关键词)。
如下这个图例,首先我们一定要明确一个结点的内容包括哪些部分,将这些看作整体,而不是分离的各部分。示例代码如下。
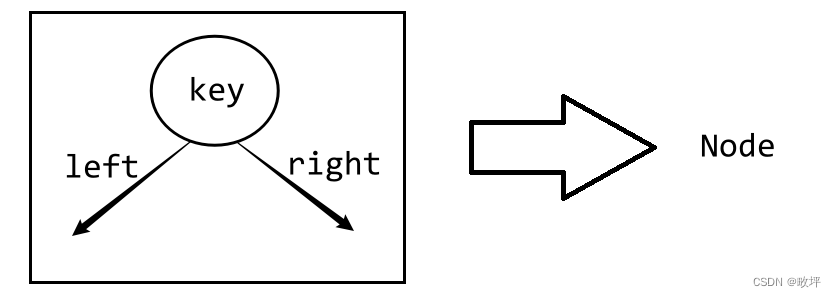
template<class K>
struct BSTreeNode
{BSTreeNode(const K key = K()):_key(key), _left(nullptr), _right(nullptr){}K _key;BSTreeNode<K>* _left;BSTreeNode<K>* _right;
};(补充:上面我们解决了结点的创建,对于二叉树的创建,我们只需要用一个根结点的指针 Node* 来实现即可,具体见下面代码BSTree的成员变量。)
2. 插入数据_Insert
思路:比较大小,按搜索二叉树的排列规则插入。
注意:①结点与新结点之间的链接问题;②注意树为空的情况。
(这部分很简单不多赘述,直接看代码。另外,注意细节,并测试这段代码的准确性后再接着往下写)
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;public:bool Insert(const K& key){if (_rootp == nullptr){_rootp = new Node(key);return true;}Node* curp = _rootp;Node* parent_p = curp;while (curp){if (curp->_key > key){parent_p = curp;curp = curp->_left;}else if (curp->_key < key){parent_p = curp;curp = curp->_right;}elsereturn false;}Node* newp = new Node(key);//注意结点之间的链接问题if (parent_p->_key > key){parent_p->_left = newp;}else{parent_p->_right = newp;}return true;}
private:Node* _rootp = nullptr;
}3. 中序遍历_InOrder
复习一下中序遍历:即 左子树(递归往下拆) 根 右子树(递归往下拆) 的顺序。
注意:这个函数肯定需要传递参数,即某个结点的指针。然后该函数将从这个传递来的参数的结点指针为根结点向下遍历,一般我们需要从整个树的根开始遍历,但是该搜索二叉树的根结点 (_rootp) 是私有成员无法访问。这个问题可以通过多种方式解决,我们这里采用“套一层”的方式。具体看代码实现。
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:void _InOrder(Node* rootp){if (rootp == nullptr)return;_InOrder(rootp->_left);std::cout << rootp->_key << " ";_InOrder(rootp->_right);}void InOrder(){return _InOrder(_rootp);//"套一层"👉类内可以随意访问成员}private:Node* _rootp = nullptr;
};
4. 查找结点_Find
根据搜索二叉树的排列特性去找,要找的这个值比当前结点值小就去左子树找,比当前结点大就去右子树找。这个函数实现起来很简单,不多赘述,具体实现可参考下面代码。
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Find(const K& key){if (_rootp == nullptr)return false;Node* curp = _rootp;while (curp){if (curp->_key > key){curp = curp->_left;}else if (curp->_key < key){curp = curp->_right;}elsereturn true;}return false;}private:Node* _rootp = nullptr;
};
5. 删除结点_Erase(难点⭐)
先找到结点,再删除。下面分析删除的思路。ps.以下对于 要被删除的结点 简称为 del.
思路:1.对于没有叶子结点的结点我们可以直接删除;
2.没有右子树的情况:我们可以让 del 的 parent 结点来接管 del 的 leftchild。同时,我们还需要判断 del 为 parent 的 rightchild 还是 leftchild。图解如下,下图中“断开链接”只是形象的说法,实现的时候只需要将 parent 的 child结点的指针直接覆盖即可。(注意 del 为 整个树的根结点 的情况→我们需要选择一个结点为新的根节点)

3.没有左子树的情况:同理(同没有右子树的分析)。(注意 要被删除的结点 是 整个树的根结点 的情况)

4.左右子树都有的情况: 找左子树的最大结点或者右子树的最小节点与要删除的结点交换。左子树的最大结点即该子树的最右叶子结点,右子树的最小结点即该子树的最左叶子结点。
找左子树的最大结点或者右子树的最小节点与要删除的结点交换。左子树的最大结点即该子树的最右叶子结点,右子树的最小结点即该子树的最左叶子结点。
如下图,选择 13 或者 9 与 10 交换都可以。
9 作为左子树中最大的结点,满足①大于左子树所有结点;②小于右子树所有节点。
13 作为右子树中最小的结点,满足①大于左子树所有结点;②小于右子树所有节点。

如上图所示,图中 the one 即为我们找到的子树中可以与 要被删除的结点 交换的结点(左子树的最大结点或者右子树的最小节点)
明确整体上的思路之后,我们来看具体怎么实现👇 (如有疑惑请参看注释)(使用swap函数记得声明头文件)
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;public:bool Erase(const K& key){if (_rootp == nullptr)return false;Node* curp = _rootp;Node* parent_p = nullptr;while (curp){if (curp->_key > key){parent_p = curp;curp = curp->_left;}else if (curp->_key < key){parent_p = curp;curp = curp->_right;}else{Node* del_nodep = curp;//找到了//进行删除//左右子树都没有的情况不需要单独判断,这个情况可以归属于没有 左子树/右子树 的情况if (del_nodep->_left == nullptr)//没有左子树的情况{if (parent_p == nullptr)_rootp = del_nodep->_right;else if (parent_p->_left == del_nodep)parent_p->_left = del_nodep->_right;elseparent_p->_right = del_nodep->_right;delete del_nodep;}else if (del_nodep->_right == nullptr){if (parent_p == nullptr)_rootp = del_nodep->_left;else if (parent_p->_left == del_nodep)parent_p->_left = del_nodep->_left;elseparent_p->_right = del_nodep->_left;delete del_nodep;}else//左右子树都存在的情况{//找到适合替换要被删除的结点的结点。//这里选择del_nodep的右树的最小结点,即右树的最左结点Node* subLeft_p = del_nodep->_right;Node* Left_parent_p = del_nodep;while (subLeft_p->_left){Left_parent_p = subLeft_p;subLeft_p = subLeft_p->_left;}std::swap(subLeft_p->_key, del_nodep->_key);del_nodep = subLeft_p;if (Left_parent_p->_right == del_nodep)Left_parent_p->_right = del_nodep->_right;elseLeft_parent_p->_left = del_nodep->_left;delete del_nodep;}return true;//删除成功}}return false;}
private:Node* _rootp = nullptr;
};
说明:增删查改的“改”
搜索二叉树由于本身的特性是不可以在结点原本的数值上进行修改的。否则可能会破坏搜索二叉树。因此没有修改的相关函数。
6. 递归版_recursion
下面我们用递归的方式来实现“增删查”。(函数名后带‘R’,用于区分递归版本与非递归版本)
递归实际上是通过参数的改变来达到“向下递归”的效果的,实现递归版本肯定要传递结点的指针,这里我们统一通过“套一层”的方式解决。如下代码。
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool FindR(const K& key){return _FindR(_rootp, key);}bool InsertR(const K& key){return _InsertR(_rootp, key);}bool EraseR(const K& key){return _EraseR(_rootp, key);}
private:bool _FindR(Node* rootp, const K& key){//}bool _InsertR(Node*& rootp, const K& key){//}bool _EraseR(Node*& rootp, const K& key){//}
private:Node* _rootp = nullptr;
};
1)_FindR
思路:根据搜索二叉树的特性。首先判断当前结点是不是要找的结点,如果不是,若比这个要找的结点比这个结点小就递归去左树找;若比这个要找的结点大就递归去右树找。找到空结点即为没找到。
bool _FindR(Node* rootp, const K& key)
{if (rootp == nullptr)return false;if (rootp->_key == key)return true;if (rootp->_key > key)return _FindR(rootp->_left, key);else if (rootp->_key < key)return _FindR(rootp->_right, key);
}2)_InsertR
思路:遵循搜索二叉树的特性。先找到合适位置再插入,要插入的结点比当前结点小就递归到左子树插入,比当前结点大就递归到右子树插入。一直到找到空位置(nullptr)即可插入。(ps.不允许插入重复值)
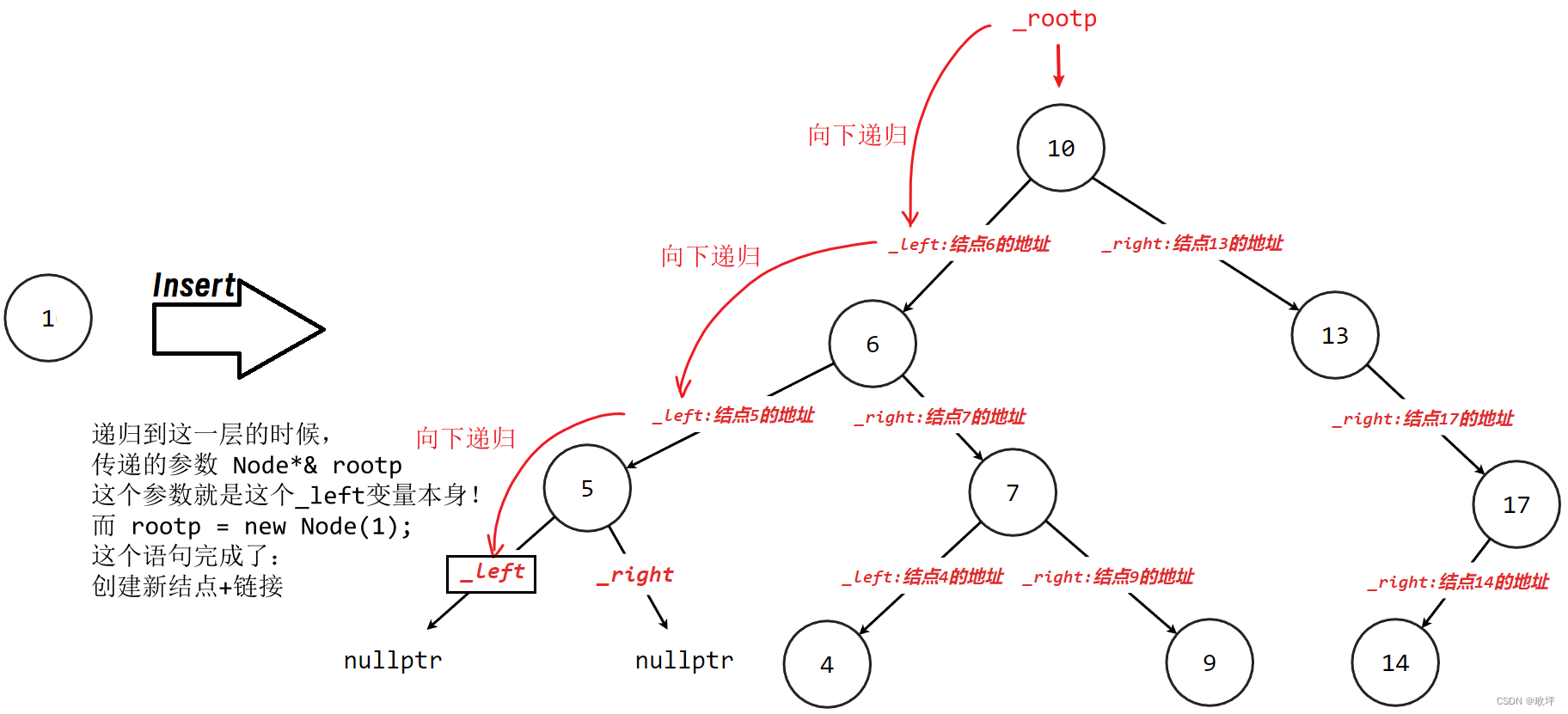
注意:关于链接的问题,我们可以通过引用传参巧妙地解决。为了方便理解,这里可以把引用传参看作传递了参数本身,而不是参数的一份拷贝。
bool _InsertR(Node*& rootp, const K& key)
{if (rootp == nullptr){rootp = new Node(key);return true;}if (rootp->_key == key)return false;if (rootp->_key > key){return _InsertR(rootp->_left, key);}else if (rootp->_key < key){return _InsertR(rootp->_right, key);}
}再次说明:Node* rootp 传值传参 是 将要传过来的指针变量的内容拷贝一份给 rootp,它们分别是两个指针变量;Node*& rootp 传引用传参 是 将要穿过的指针变量本身(也可以理解为这个指针变量的别名)传递过来,rootp就是这个指针变量,它们就是同一个指针变量。
3)_EraseR
基本思路:先找到要删除的结点,没找到就直接返回 false,找到了就进行删除。
递归思路:要删除的结点值 key 比当前结点小就递归到左树删除;比当前结点大就递归到右树删除;等于当前结点就对这个结点进行删除。
bool _EraseR(Node*& rootp, const K& key)
{if (rootp == nullptr)return false;if (rootp->_key > key){return _EraseR(rootp->_left, key);}else if (rootp->_key < key){return _EraseR(rootp->_right, key);}else{Node* del_nodep = rootp;if (del_nodep->_left == nullptr)//左子树为空或左右子树为空{rootp = del_nodep->_right;delete del_nodep;}else if (del_nodep->_right == nullptr)//右子树为空{rootp = del_nodep->_left;delete del_nodep;}else//左右子树都不为空{Node* subLeft = del_nodep->_right;while (subLeft->_left){subLeft = subLeft->_left;}std::swap(subLeft->_key, del_nodep->_key);return _EraseR(rootp->_right, key);}}
}对于左右子树为空/左子树为空/右子树为空的情况:(以下图情况为例分析)
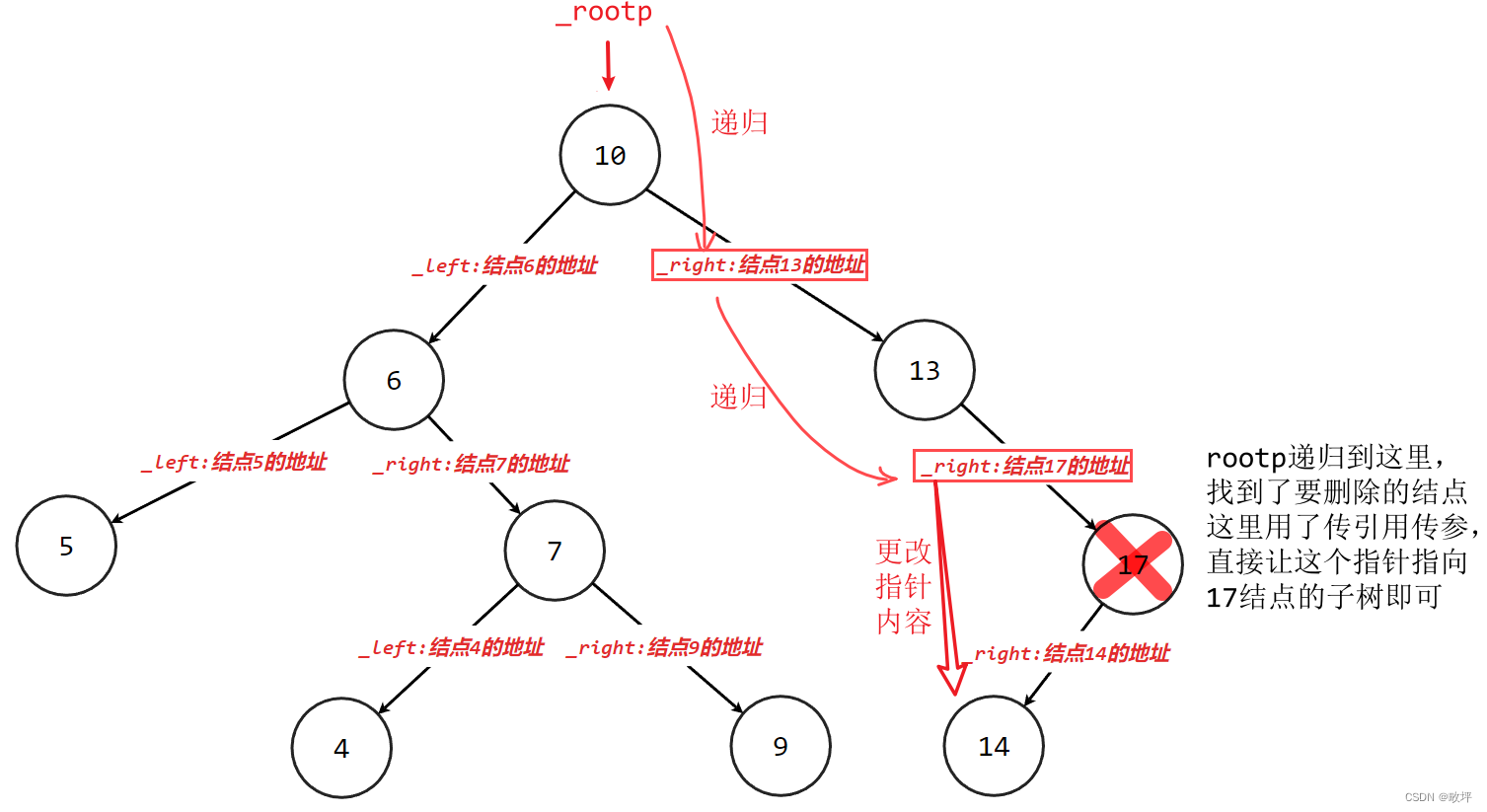
对于左右子树都不为空的情况:(以下图情况为例分析)
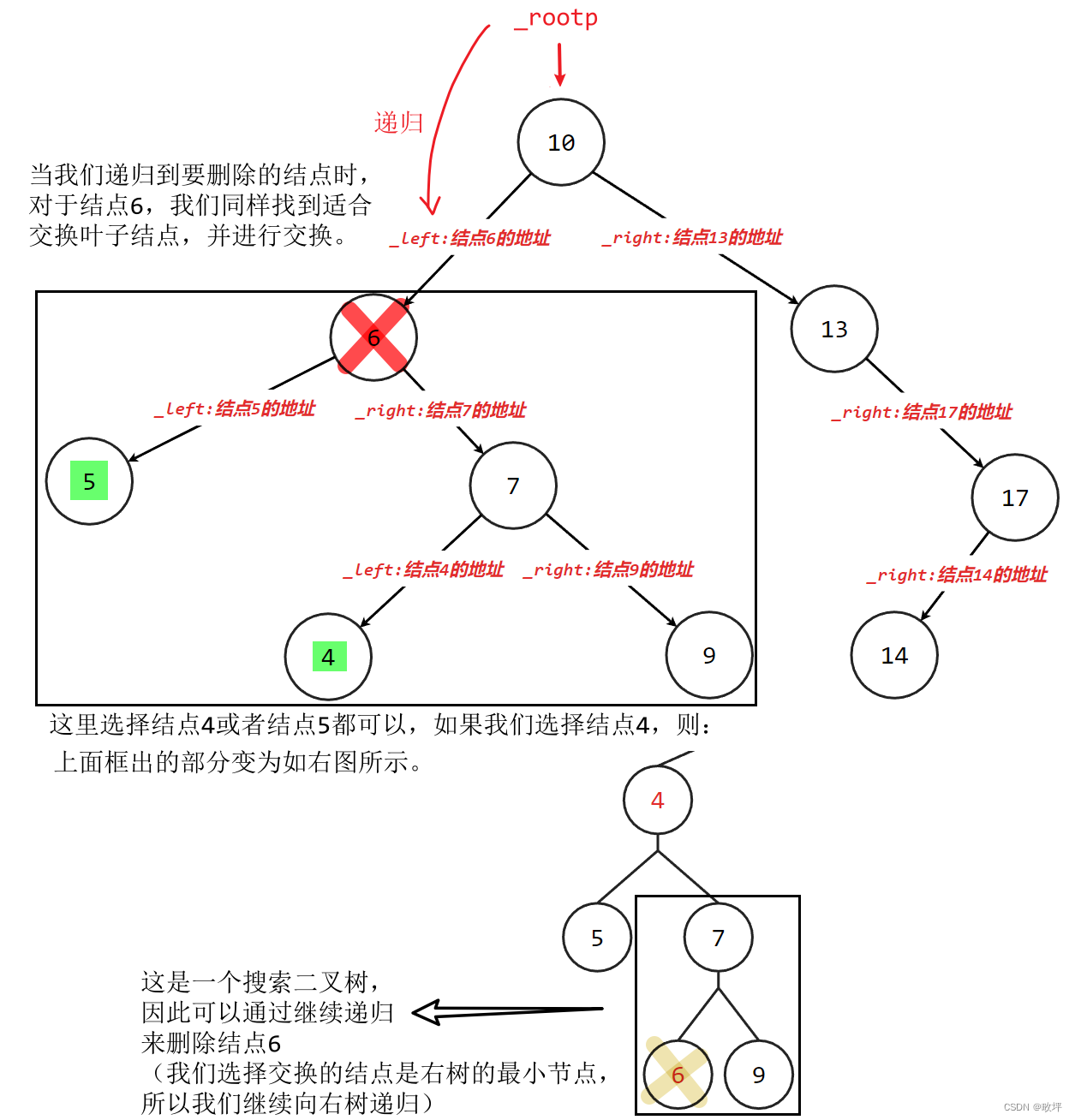
END