LeetCode-1486. 数组异或操作【位运算 数学】
- 题目描述:
- 解题思路一:暴力很简单。
- 解题思路二:优化!时间复杂度:O(1)。注释丰富,明了。
- 解题思路三:精简版!
题目描述:
给你两个整数,n 和 start 。
数组 nums 定义为:nums[i] = start + 2*i(下标从 0 开始)且 n == nums.length 。
请返回 nums 中所有元素按位异或(XOR)后得到的结果。
示例 1:
输入:n = 5, start = 0
输出:8
解释:数组 nums 为 [0, 2, 4, 6, 8],其中 (0 ^ 2 ^ 4 ^ 6 ^ 8) = 8 。
“^” 为按位异或 XOR 运算符。
示例 2:
输入:n = 4, start = 3
输出:8
解释:数组 nums 为 [3, 5, 7, 9],其中 (3 ^ 5 ^ 7 ^ 9) = 8.
示例 3:
输入:n = 1, start = 7
输出:7
示例 4:
输入:n = 10, start = 5
输出:2
提示:
1 <= n <= 1000
0 <= start <= 1000
n == nums.length
解题思路一:暴力很简单。
class Solution:def xorOperation(self, n: int, start: int) -> int:ans = startfor i in range(1, n):# ans ^= start + 2 * ians = ans ^ (start + 2 * i)return ans
时间复杂度:O(n)
空间复杂度:O(1)
解题思路二:优化!时间复杂度:O(1)。注释丰富,明了。
首先要知道:

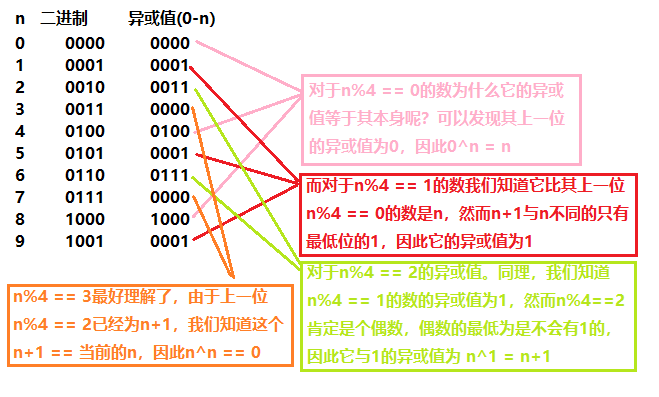
解释一下性质五: 0^1^2^3 = 0, 4^5^6^7=0, 8^9^10^11=0 .....以此下去, 有这么个规律存在. 为什么呢? 可以用结合律,把前边两个数和后边两个数分开运算。 然后把数字转换成二进制,4的倍数的部分和最后两位没有关系,4个数字都是相同的, 就比如> 四个数字依次是xxxx00,xxxx01,xxxx10,xxxx11 然后取异或 前两个数的结果就是01,后两个数的异或结果还是01, 01和01异或,结果当然就是0啦

观察公式可以知道,这些数的奇偶性质相同,因此它们的二进制表示中的最低位或者均为 1,或者均为 0。于是我们可以把参与运算的数的二进制位的最低位提取出来单独处理。当且仅当 start 为奇数,且 n 也为奇数时,结果的二进制位的最低位才为 1。
e = n & start & 1 # 取最低位

为啥 sumXor() 的逻辑是这样的:
看代码注释也可以 !
class Solution:def xorOperation(self, n: int, start: int) -> int:# 计算目标 start ^ (start + 2) ^ (start + 4) ^ ... ^ (start + 2(n-1))# 1.提取一个2出来,并且令s = start//2,得到:# (s ^ (s+1) ^ (s+2) ^ ... ^ (s+n-1)) x 2 + e# 2.这里的e是计算目标的最低位,依据计算目标的特点,e取决于start和n。当且仅当 start 为奇数,且 n 也为奇数时,结果的二进制位的最低位才为 1。# e = n & start & 1# 3.我们只需要计算:cur = (s ^ (s+1) ^ (s+2) ^ ... ^ (s+n-1))# 依据性质4和性质3:x ^ y ^ y = x 和 (x ^ y) ^ z = x ^ (y + z)# 只需计算:(0 ^ 1 ^ 2 ^ 3 ^ ... ^ s - 1)^( 0 ^ 1 ^ 2 ^ 3 ^ …… ^ s - 1 ^ s ^ (s+1) ^ (s+2) ^ ... ^ (s+n-1))# 便可以得到 (s ^ (s+1) ^ (s+2) ^ ... ^ (s+n-1))# 4. (0 ^ 1 ^ 2 ^ 3 ^ ... ^ s - 1) 的计算函数sumXor(x)的逻辑:# 见函数定义注释以及图解# 5. 最终答案为cur << 1 | e# 等价于(s ^ (s+1) ^ (s+2) ^ ... ^ (s+n-1)) x 2 + edef sumXor(x):if x % 4 == 0: # 刚好剩下nreturn xif x % 4 == 1: # n ^ (n+1) = 1return 1if x % 4 == 2: # n ^ (n+1) ^ (n+2) = 1 ^ (n+2) !!!注意此时x为(n+2)return x + 1if x % 4 == 3: # n ^ (n+1) ^ (n+2) ^ (n+3) = 0 全部消掉return 0e = n & start & 1 # 取最低位s = start >> 1cur = sumXor(s-1) ^ sumXor(s+n-1)return cur << 1 | e
时间复杂度:O(1)
空间复杂度:O(1)
解题思路三:精简版!
class Solution:def xorOperation(self, n: int, start: int) -> int:def sumXor(x):if x % 4 == 0:return xif x % 4 == 1:return 1if x % 4 == 2:return x + 1if x % 4 == 3:return 0e = start & n & 1s = start // 2ans = sumXor(s-1) ^ sumXor(s+n-1)return ans * 2 + e
时间复杂度:O(n)
空间复杂度:O(n)



♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠ ⊕ ♠