力扣刷题 旋转矩阵
- 二维矩阵按圈遍历(顺时针 or 逆时针)遍历
- 59. 旋转矩阵Ⅱ
- 54. 旋转矩阵
- 剑指 Offer 29. 顺时针打印矩阵
二维矩阵按圈遍历(顺时针 or 逆时针)遍历
下面的题目的主要考察点都是,二维数组从左上角开始顺时针(或者逆时针)按圈遍历数组的过程。顺时针按圈遍历的过程如下:
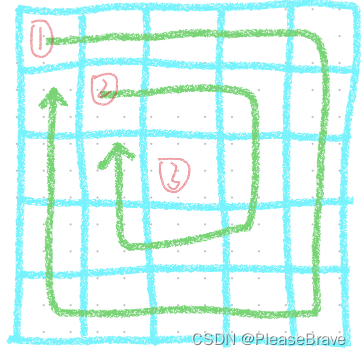
对于每一圈,分为四条边,循环遍历就好。这时,对于四个角的元素的处理,可以将四条边的遍历分为以下两种情况:
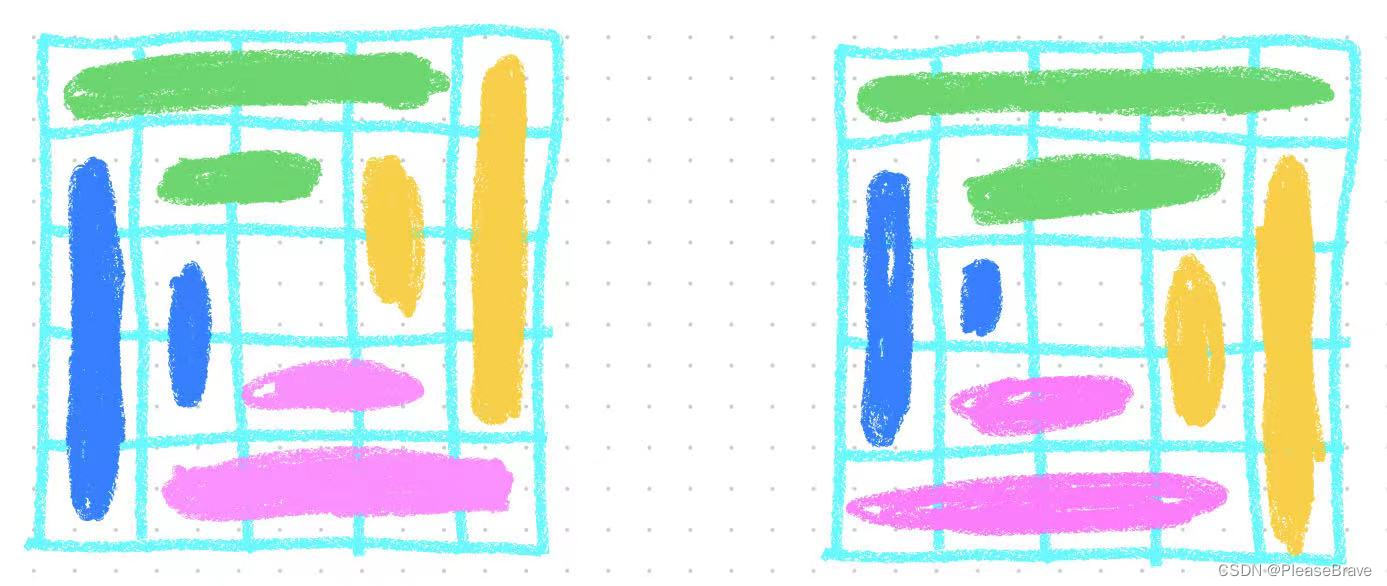
- 第一种:每条边都从对应一角开始,遍历对应边的时候,最后一个元素留给下一条边;比如第一条绿色的边,最后一个元素就没有访问;第二条黄色的边就从左上角元素开始,相应的最左下角的元素没有访问;以此类推;
代码实现(C++):
//count表示访问了的元素个数,控制遍历完数组没有while(count <= n*n){//i,j是行、列的下标,每次总是从[0,0],[1,1]开始一圈循环int i = p;int j = p;//每圈最上面一条边的遍历 while(j < n - 1 - p){//因为最一个元素[i][n-1-p]留给下一条边,因此这里不取等ans[i][j++] = count++;}//每圈最右边的一条边的遍历while(i < n - 1 - p){//因为最一个元素[n-1-p][j]留给下一条边,因此这里不取等ans[i++][j] = count++;}//每圈最下面一条边的遍历while(j > p){//因为最后一个元素[i][p]留给下一条边,因此这里不取等ans[i][j--] = count++;}//每圈最左边的一条边的遍历while(i > p){//因为[p][p]就是这一圈的起始点,在第一条边就遍历过了,所以这里取等ans[i--][j] = count++;}p++;}
- 第二种:遍历每一条边时,就将该边所有未被访问的元素全部遍历;比如第一条绿色的,最后一个元素就访问了;然后第二条边黄色的就对应列的第二个开始,因为第一个已经被访问了;之后的边以此类推;
代码实现(C++):
//count控制遍历完了没有while(count <= n*n){ //遍历最上边的一条边 for(int i = left; i <= right ; i++){ans[top][i] = count++;}//遍历完后top++top++;//遍历最右边的边for(int i = top; i <= bottom; i++){ans[i][right] = count++;}//遍历完后right--right--;//遍历最下边的边for(int i = right; i >= left ;i--){ans[bottom][i] = count++;}//遍历完后bottom--bottom--;//遍历最左边一条边for(int i = bottom; i >= top; i--){ans[i][left] = count++;}//遍历完后left++left++;}
59. 旋转矩阵Ⅱ
螺旋矩阵 II
题目内容如下:
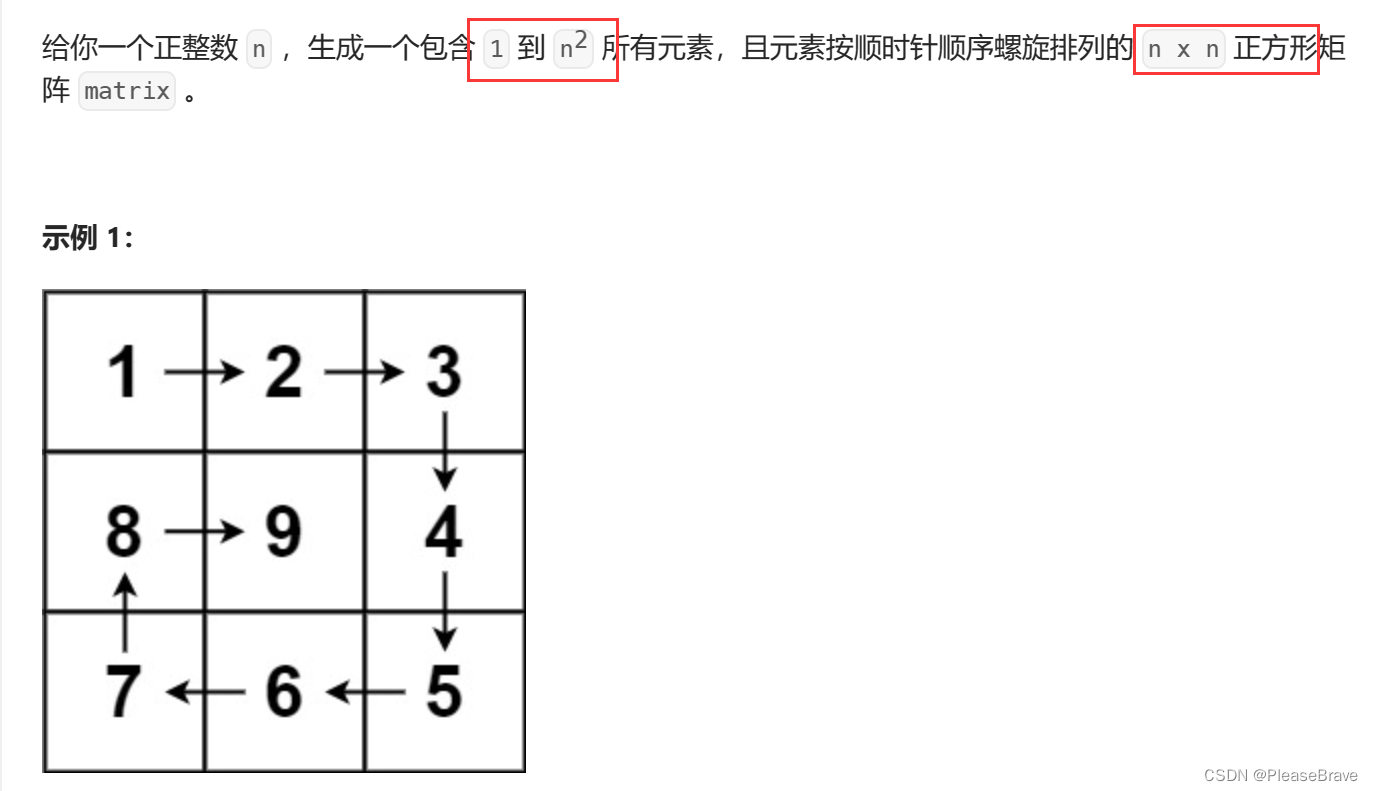
注意点是n*n的正方形矩阵,行列数量相同。只要按照前面提到的顺时针访问数组的过程中,给每个位置递增赋值就好。按圈遍历的过程中,需要循环遍历多少次呢?答案是(n+1)/2次。
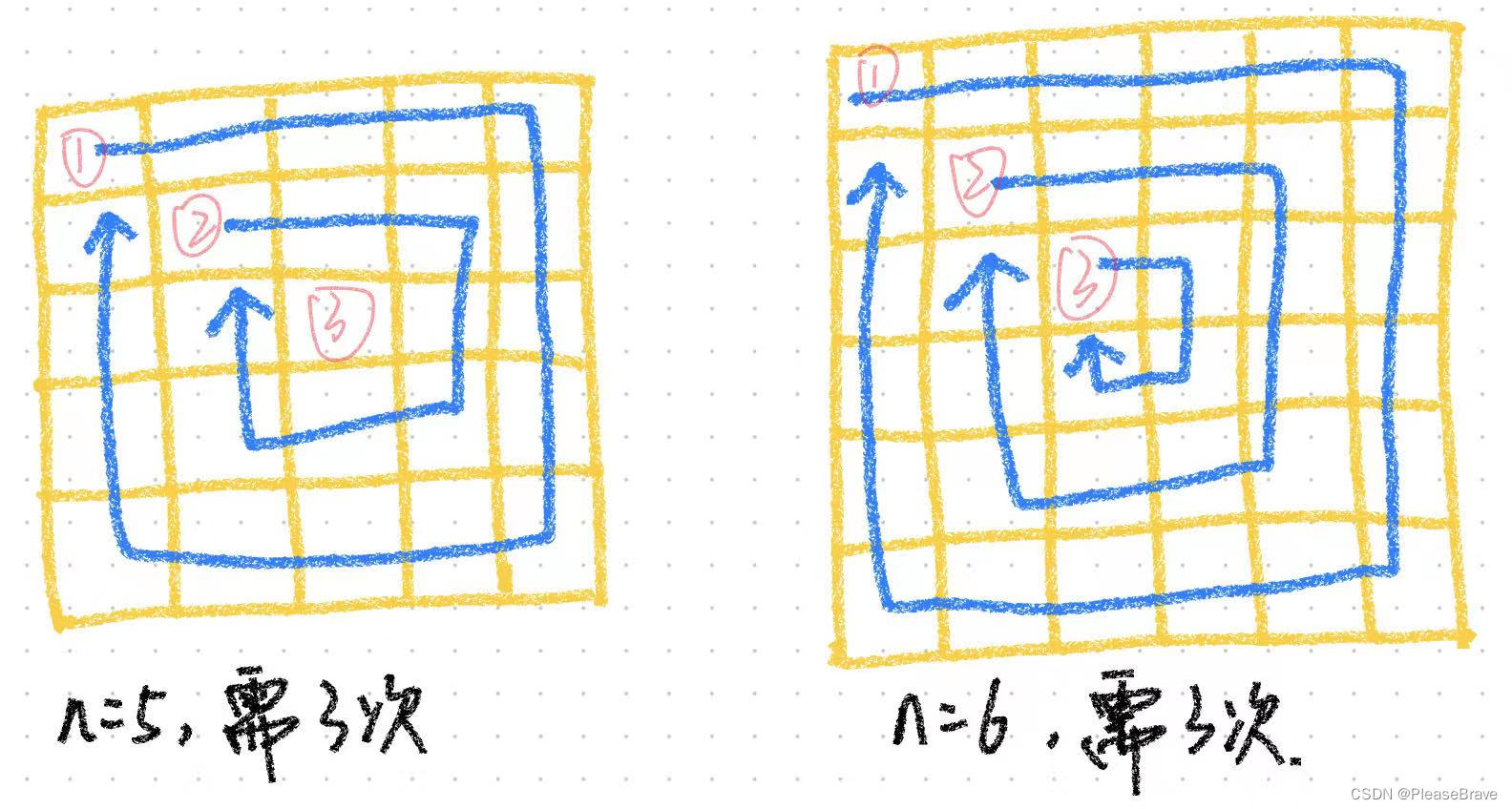
但是按照上面提到的第一种俺圈遍历的过程中:
- n为偶数时,每次减少2行,2 列,最后刚好遍历完;
- n为奇数时,最后一次只有单独一个,因为每条边的最后一个元素都留给下一条边了,所以实际上没有哪条边去遍历了。比如n=5,p=2时,i=2,j=2,n-1-p=2,由于i=j=p=n-1-p,第一种代码提到的四种循环条件都不满足。所以在最后要单独给这个位置赋值。代码如下(C++):
class Solution {
public:vector<vector<int>> generateMatrix(int n) {int count = 1;int i, j, p;vector<vector<int>> ans(n,vector<int>(n));//因为n为奇数的最后一圈在最后单独赋值,所以这里p<n/2就好for(int p = 0; p < n/2; p++){i = p;j = p; while(j < n - 1 - p){ans[i][j++] = count++;}while(i < n - 1 - p){ans[i++][j] = count++;}while(j > p){ans[i][j--] = count++;}while(i > p){ans[i--][j] = count++;}}//n为奇数时,最后一个位置(最中间)单独赋值if( n%2 != 0){ans[n/2][n/2] = count;}return ans;}
};
对于第二种按圈遍历的过程,因为用top//bottom//left//right来控制,最后中间位置的能够遍历到,不需要额外的处理,代码如下(C++):
class Solution {
public:vector<vector<int>> generateMatrix(int n) { vector<vector<int>> ans(n,vector<int>(n));int left = 0, right = n - 1;int top = 0, bottom = n -1;int count = 1;while(count <= n*n){int i;for(i = left; i <= right ; i++){ans[top][i] = count++;}top++;for(i = top; i <= bottom; i++){ans[i][right] = count++;}right--;for(i = right; i >= left ;i--){ans[bottom][i] = count++;}bottom--;for(i = bottom; i >= top; i--){ans[i][left] = count++;}left++;}return ans;}
};
54. 旋转矩阵
54. 旋转矩阵
题意如下: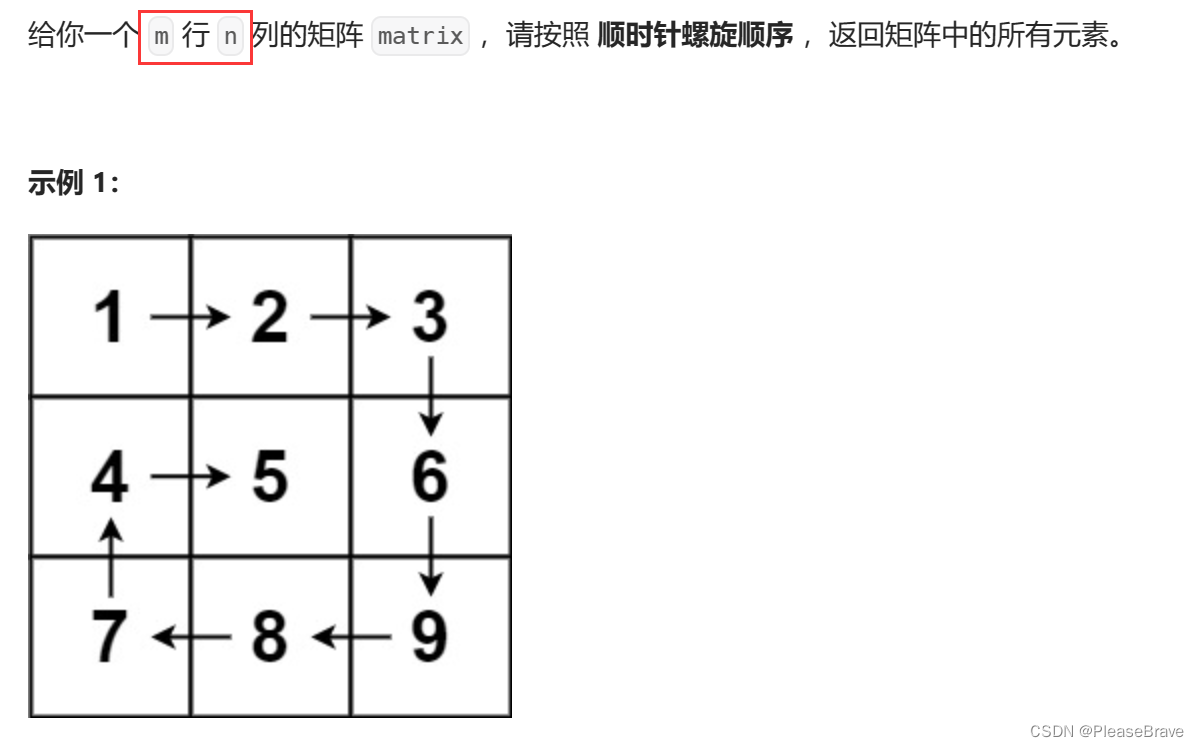
跟上一题不同的点在于,矩阵由nn变成了==mn==,m和n不一定相等,即现在的矩阵可能不再是正方形的了。那么根据m(行数)///n(偶数)是奇数还是偶数?大小关系可以分为以下七种情况:
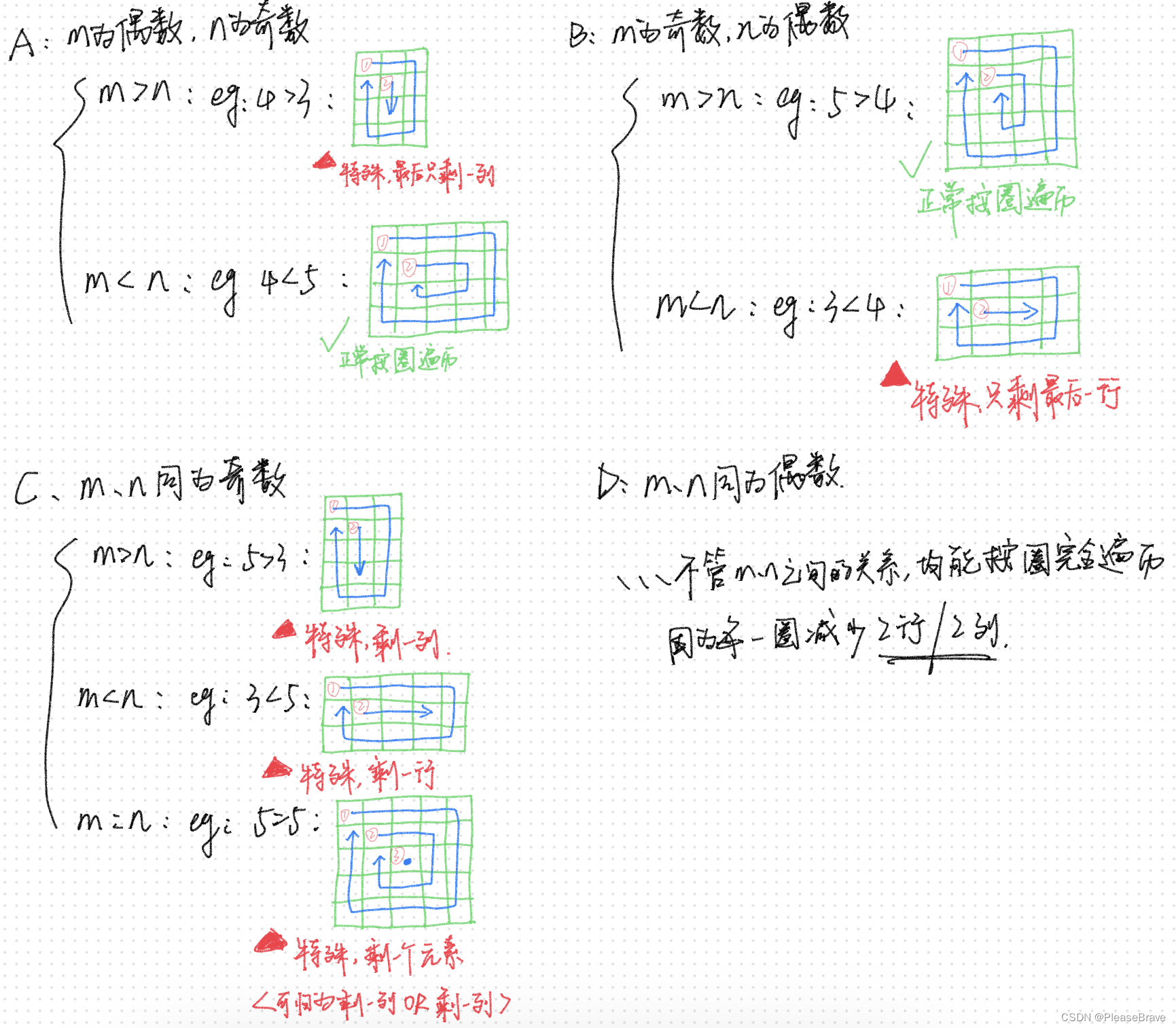
分析这7种情况,得出结论,只要满足如下两种情况之一,最后就有需要单独处理的:
- m<n并且m是奇数(不管n是奇是偶),最终会多出来一行(因为m行数更小,行先结束圈的遍历,但是列还有更多的,所以多出来一行);
- n<m并且n是奇数(不管m是奇是偶),最终会多出来一列(因为n列数更小,列先结束圈的遍历,但是行还有很多,所以多出来一列);
(m=n同为奇数的情况可以归为上述任意一种)。
代码实现的过程,就是最终会判断一下是否出现上面的情况,然后单独处理这一行///这一列就好,代码如下:
class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int step_i = 0, step_j = 0, index = 0;int m = matrix.size(), n = matrix[0].size();vector<int> ans(m*n);//与上一题代码基本一致,只是<m/2和<n/2需要单独判断while(step_i < m/2 && step_j < n/2){int i = step_i;int j = step_j;for(; j < n - 1 -step_j; j++){ans[index++] = matrix[i][j];}for(; i < m - 1 - step_i; i++){ans[index++] = matrix[i][j];}for(; j > step_j; j--){ans[index++] = matrix[i][j];}for(; i > step_i ;i--){ans[index++] = matrix[i][j];}step_i++;step_j++;}//行是奇数并且m<n,剩下一行if(m%2 != 0 && step_i == m/2){for(int j = step_j; j < n - step_j; j++)ans[index++] = matrix[step_i][j];}//列是奇数并且n<m,剩下一列else if(n%2 != 0 && step_j == n/2){for(int i = step_i; i < m -step_i; i++ )ans[index++] = matrix[i][step_j];} return ans; }
};
如果用第二种按圈遍历的方法,更简单,只是在大循环内依次进行的四个小循环,需要在最后两个循环添加额外的循环条件:
class Solution {
public:vector<int> spiralOrder(vector<vector<int>>& matrix) {int m = matrix.size(), n = matrix[0].size();vector<int> ans(m*n);int left = 0, right = n - 1;int top = 0, bottom = m - 1;int index = 0;while(index < m*n){for(int i = left; i <= right; i++){ans[index++] = matrix[top][i];}top++;for(int i = top; i <= bottom; i++){ans[index++] = matrix[i][right];}right--;//需要添加额外的条件 index < m*n (根据实际题目要求选择对应的约束条件for(int i = right; i >=left && index < m*n; i--){ans[index++] = matrix[bottom][i];}bottom--;//需要添加额外的条件index < m*n (根据实际题目要求选择对应的约束条件for(int i = bottom; i >= top && index < m*n; i--){ans[index++] = matrix[i][left];}left++;}return ans;}
};
为什么要添加这两个?请看下例:
如果不在内层的四个循环的后两个中添加额外的限制,就会出现多遍历的情况。
剑指 Offer 29. 顺时针打印矩阵
剑指 Offer 29. 顺时针打印矩阵
和54是一样的题目,只是注意m和n可能等于0。