概念

之前的回归的变量是连续的数值变量；而Logistics回归是二元离散值，用来解决二分类问题。

理论分析

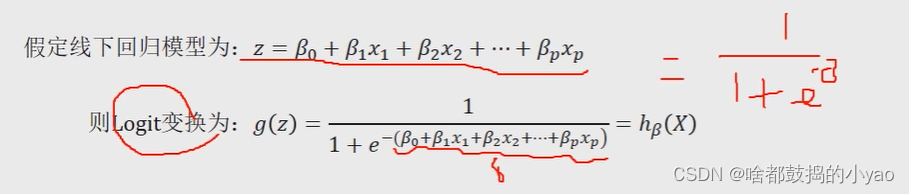
上式中的hβ(X)也被称为Loqistic回归模型，它是将线性回归模型的预测值经过非线性的Logit函数转换为[0,1]之间的概率值。

其函数图像为：

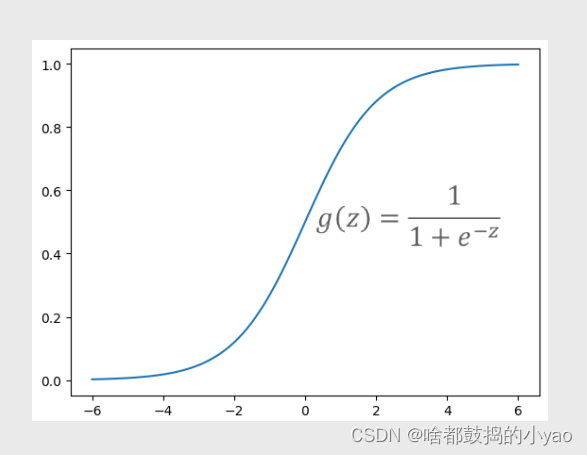
其中，z∈(-∞,+∞)。当z趋于正无穷大时，e**-z将趋于0，进而导致g(z)逼近于1；相反，当z趋于负无穷大时，e**-z会趋于正无穷大，最终导致g(z)逼近于0；当z=0时，e**-z=1，所以得到g(z)=0.5。

我们对模型进行转化：

参数求解过程：
不难发现y=1的时候为p，y=0的时候为1-p，那么可以等价为（将离散状态变为函数状态）

进行极大似然估计（因为没有残差函数）:
构造似然函数，有n行数据，每行数据的概率发生累乘起来

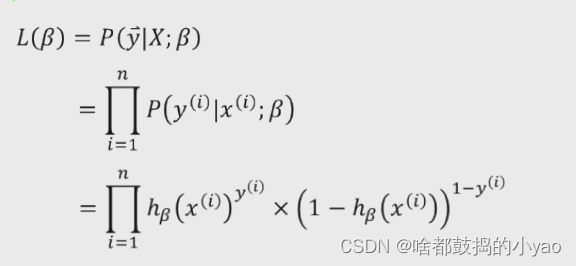
我们对其进行对数化，优化计算：
log(x1x2x3)=logx1+logx2+logx3

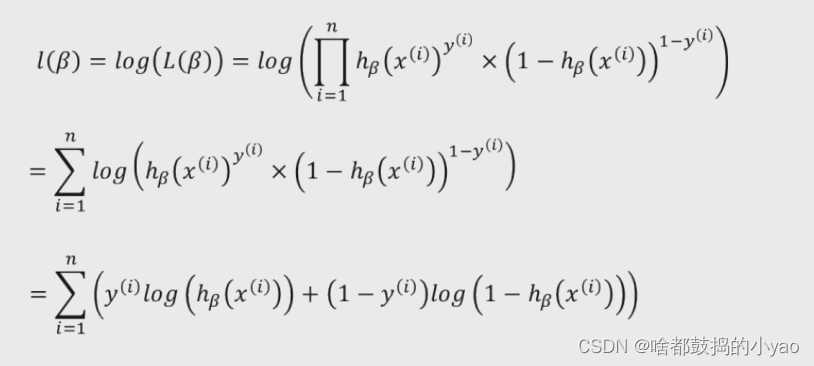
梯度下降：
我们只需要将其变为负数，就有极大求为了极小值，通过此来进行梯度下降的算法。

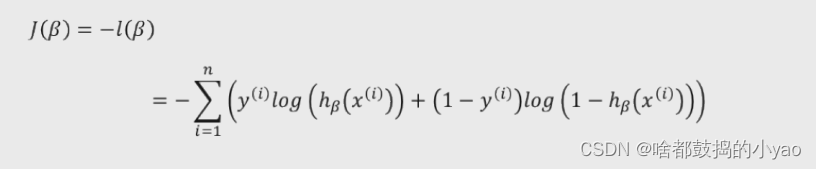
对其求偏导，每一个参数β做梯度下降

其中，α为学习率，也称为参数βj变化的步长，通常步长可以取0.1，0.05，0.01等。如果设置的α过小，会导致βj变化微小，需要经过多次迭代，收敛速度过慢；但如果设置的过大，就很难得到理想的βj值，进而导致目标函数可能是局部最小。

求出的参数含义：
通过建模可以得到对应的系数B和，则假设影响是否患癌的因素有性别和肿瘤两个变量Logistic回归模型可以按照事件发生比的形式改写为:

其中p/(1-p)叫优势比/发生比。

分别以性别变量x1和肿瘤体积变量x2为例，解释系数β1和β2的含义。假设性别中男用1表示，女用0表示，则:

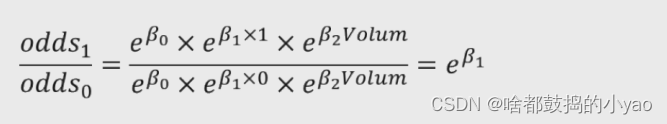
所以，性别变量的发生比率为e** β1，表示男性患癌的发生比约为女性患癌发生比的e**β1倍。

对于连续型的自变量而言，参数解释类似，假设肿瘤体积为Volum0，当肿瘤体积增加1个单位时体积为Volum0+1，则：

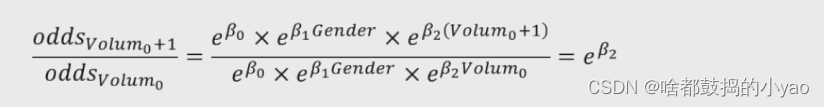
所以，在其他变量不变的情况下，肿瘤体积每增加一个单位，将会使患癌发生比变化e**β2倍。

模型评估

混淆矩阵

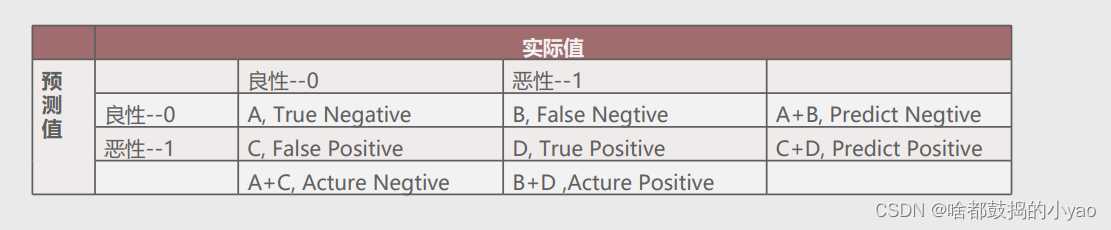
A：表示正确预测负例的样本个数，用TN表示。
B：表示预测为负例但实际为正例的个数，用FN表示。
C：表示预测为正例但实际为负例的个数，用FP表示。
D：表示正确预测正例的样本个数，用TP表示。
准确率：表示正确预测的正负例样本数与所有样本数量的比值，即(A+D)/(A+B+C+D)。
正例覆盖率：表示正确预测的正例数在实际正例数中的比例，即D/(B+D)。
负例覆盖率：表示正确预测的负例数在实际负例数中的比例，即A/(A+C)。
正例命中率：表示正确预测的正例数在预测正例数中的比例，即D/(C+D)，

正例：指的是非常关心的例子叫做正例，这里面就是恶性。

ROC曲线

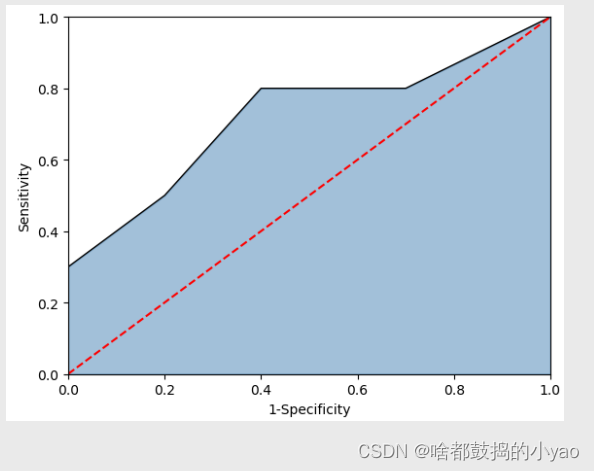
图中的红色线为参考线，即在不使用模型的情况下，Sensitivity（正例覆盖率） 和 1-Specificity（1-负例覆盖率） 之比恒等于 1。通常绘制ROC曲线，不仅仅是得到左侧的图形，更重要的是计算折线下的面积，即图中的阴影部分，这个面积称为AUC。在做模型评估时，希望AUC的值越大越好，通常情况下，当AUC在0.8以上时，模型就基本可以接受了。

KS曲线

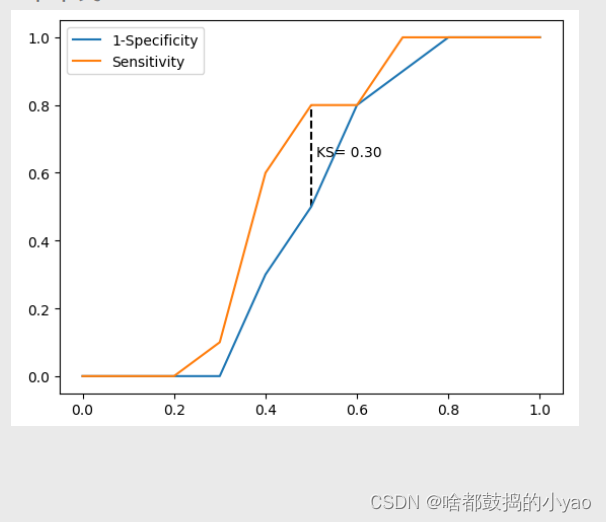
x轴叫阈值，图中的两条折线分别代表各分位点下的正例覆盖率和1-负例覆盖率，通过两条曲线很难对模型的好坏做评估，一般会选用最大的KS值作为衡量指标。KS的计算公式为：KS = Sensitivity-(1- Specificity) = Sensitivity+ Specificity-1。对于KS值而言，也是希望越大越好，通常情况下，当KS值大于0.4时，模型基本可以接受。

函数

LogisticRegression(tol=0.0001, fit_intercept=True,class_weight=None, max_iter=100)
tol：用于指定模型跌倒收敛的阈值
fit_intercept：bool类型参数，是否拟合模型的截距项，默认为True
class_weight：用于指定因变量类别的权重，如果为字典，则通过字典的形式{class_label:weight}传递每个类别的权重；如果为字符串’balanced’，则每个分类的权重与实际样本中的比例成反比，当各分类存在严重不平衡时，设置为’balanced’会比较好；如果为None，则表示每个分类的权重相等
max_iter：指定模型求解过程中的最大迭代次数， 默认为100

示例

1. 我们先进行数据训练

# 导入第三方模块
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn import linear_model# 读取数据
sports = pd.read_csv(r'D:\pythonProject\data\Run or Walk.csv')
# 提取出所有自变量名称
predictors = sports.columns[4:]
# 构建自变量矩阵
X = sports.loc[:,predictors]
# 提取y变量值
y = sports.activity
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)# 利用训练集建模
sklearn_logistic = linear_model.LogisticRegression()
sklearn_logistic.fit(X_train, y_train)
# 返回模型的各个参数（截距项和偏回归系数）
print(sklearn_logistic.intercept_, sklearn_logistic.coef_)

输出：

[4.36637441] [[ 0.48695898 6.87517973 -2.44872468 -0.01385936 -0.16085022 0.13389695]]

2. 进行下预测查看效果

# 模型预测
sklearn_predict = sklearn_logistic.predict(X_test)
# 预测结果统计
pd.Series(sklearn_predict).value_counts()

输出：

0 12119 # 步行状态
1 10028 # 跑步状态
Name: count, dtype: int64

3. 我们来看下混淆矩阵

# 导入第三方模块
from sklearn import metrics
# 混淆矩阵
cm = metrics.confusion_matrix(y_test, sklearn_predict, labels = [0,1])
cm

输出：

array([[9969, 1122],
[2150, 8906]], dtype=int64)

计算下有用值：

Accuracy = metrics._scorer.accuracy_score(y_test, sklearn_predict)
Sensitivity = metrics._scorer.recall_score(y_test, sklearn_predict)
Specificity = metrics._scorer.recall_score(y_test, sklearn_predict, pos_label=0)
print('模型准确率为%.2f%%' %(Accuracy*100))
print('正例覆盖率为%.2f%%' %(Sensitivity*100))
print('负例覆盖率为%.2f%%' %(Specificity*100))

输出：

模型准确率为85.23%
正例覆盖率为80.55%
负例覆盖率为89.88%

4. ROC曲线

# y得分为模型预测正例的概率
y_score = sklearn_logistic.predict_proba(X_test)[:,1]
# 计算不同阈值下，fpr和tpr的组合值，其中fpr表示1-Specificity，tpr表示Sensitivity
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 计算AUC的值
roc_auc = metrics.auc(fpr,tpr)# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加边际线
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 添加文本信息
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
# 添加x轴与y轴标签
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
# 显示图形
plt.show()

输出：

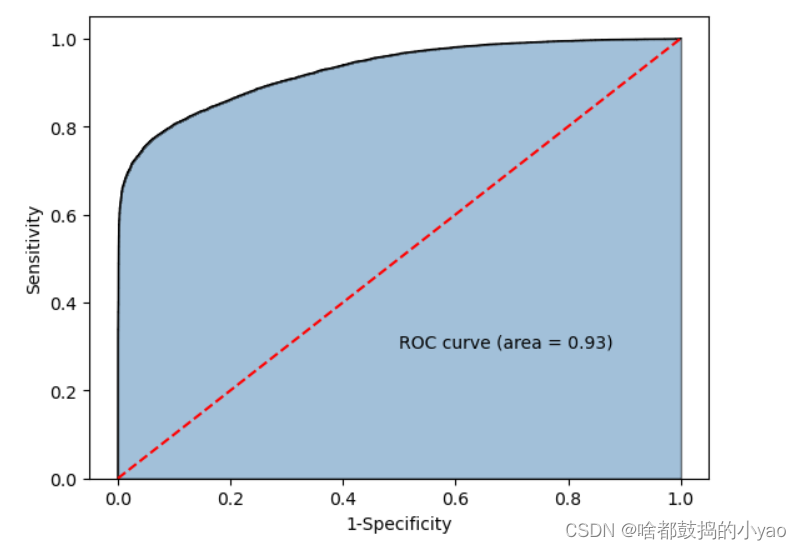
5. KS曲线

# 调用自定义函数，绘制K-S曲线
plot_ks(y_test = y_test, y_score = y_score, positive_flag = 1)

输出：

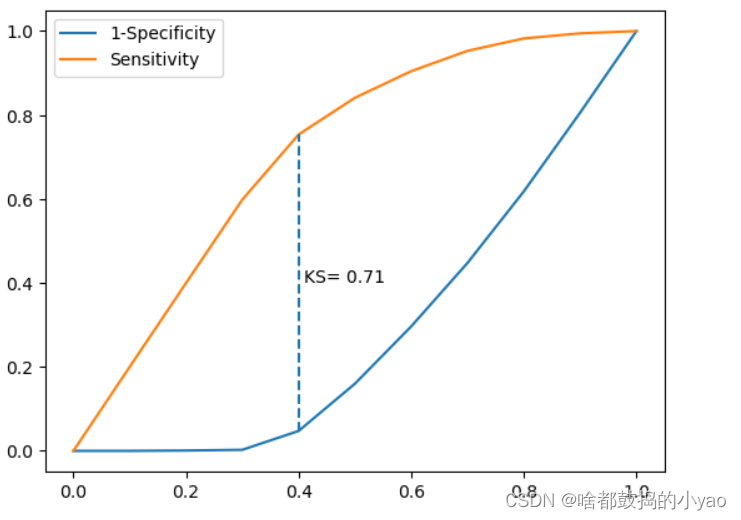
总代码：

# 导入第三方模块
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn import linear_model
from sklearn import metrics# 0.自定义绘制ks曲线的函数
def plot_ks(y_test, y_score, positive_flag):# 对y_test重新设置索引y_test.index = np.arange(len(y_test))# 构建目标数据集target_data = pd.DataFrame({'y_test':y_test, 'y_score':y_score})# 按y_score降序排列target_data.sort_values(by = 'y_score', ascending = False, inplace = True)# 自定义分位点cuts = np.arange(0.1,1,0.1)# 计算各分位点对应的Score值index = len(target_data.y_score)*cutsscores = np.array(target_data.y_score)[index.astype('int')]# 根据不同的Score值，计算Sensitivity和SpecificitySensitivity = []Specificity = []for score in scores:# 正例覆盖样本数量与实际正例样本量positive_recall = target_data.loc[(target_data.y_test == positive_flag) & (target_data.y_score>score),:].shape[0]positive = sum(target_data.y_test == positive_flag)# 负例覆盖样本数量与实际负例样本量negative_recall = target_data.loc[(target_data.y_test != positive_flag) & (target_data.y_score<=score),:].shape[0]negative = sum(target_data.y_test != positive_flag)Sensitivity.append(positive_recall/positive)Specificity.append(negative_recall/negative)# 构建绘图数据plot_data = pd.DataFrame({'cuts':cuts,'y1':1-np.array(Specificity),'y2':np.array(Sensitivity), 'ks':np.array(Sensitivity)-(1-np.array(Specificity))})# 寻找Sensitivity和1-Specificity之差的最大值索引max_ks_index = np.argmax(plot_data.ks)plt.plot([0]+cuts.tolist()+[1], [0]+plot_data.y1.tolist()+[1], label = '1-Specificity')plt.plot([0]+cuts.tolist()+[1], [0]+plot_data.y2.tolist()+[1], label = 'Sensitivity')# 添加参考线plt.vlines(plot_data.cuts[max_ks_index], ymin = plot_data.y1[max_ks_index], ymax = plot_data.y2[max_ks_index], linestyles = '--')# 添加文本信息plt.text(x = plot_data.cuts[max_ks_index]+0.01,y = plot_data.y1[max_ks_index]+plot_data.ks[max_ks_index]/2,s = 'KS= %.2f' %plot_data.ks[max_ks_index])# 显示图例plt.legend()# 显示图形plt.show()# 1.读取数据与训练
sports = pd.read_csv(r'D:\pythonProject\data\Run or Walk.csv')
# 提取出所有自变量名称
predictors = sports.columns[4:]
# 构建自变量矩阵
X = sports.loc[:,predictors]
# 提取y变量值
y = sports.activity
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)# 利用训练集建模
sklearn_logistic = linear_model.LogisticRegression()
sklearn_logistic.fit(X_train, y_train)
# 返回模型的各个参数（截距项和偏回归系数）
# print(sklearn_logistic.intercept_, sklearn_logistic.coef_)
# 模型预测
sklearn_predict = sklearn_logistic.predict(X_test)# 2.混淆矩阵
cm = metrics.confusion_matrix(y_test, sklearn_predict, labels = [0,1])
Accuracy = metrics._scorer.accuracy_score(y_test, sklearn_predict) # 模型覆盖率
Sensitivity = metrics._scorer.recall_score(y_test, sklearn_predict) # 正例覆盖率
Specificity = metrics._scorer.recall_score(y_test, sklearn_predict, pos_label=0) # 负例覆盖率# 3.ROC曲线
# y得分为模型预测正例的概率
y_score = sklearn_logistic.predict_proba(X_test)[:,1]
# 计算不同阈值下，fpr和tpr的组合值，其中fpr表示1-Specificity，tpr表示Sensitivity
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
# 绘制面积图
plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black')
# 添加ROC曲线的轮廓
plt.plot(fpr, tpr, color='black', lw = 1)
# 添加对角线
plt.plot([0,1],[0,1], color = 'red', linestyle = '--')
# 显示图形
plt.show()# 4.KS曲线
# 调用自定义函数，绘制K-S曲线
plot_ks(y_test = y_test, y_score = y_score, positive_flag = 1)