代码随想录
一、数组理论基础
二、LeetCode 704. 二分查找
三、LeetCode 27. 移除元素
四、LeetCode 977.有序数组的平方
五、LeetCode 209.长度最小的子数组
六、LeetCode 59.螺旋矩阵II
七、数组总结
一、数组理论基础
数组是存放在连续内存空间上的相同类型数据的集合。
- 数组下标都是从0开始的。
- 数组内存空间的地址是连续的
因为数组的在内存空间的地址是连续的,所以我们在删除或者增添元素的时候,就难免要移动其他元素的地址。
数组的元素是不能删的,只能覆盖。
二、二分查找 (二分法)
题目:. - 力扣(LeetCode)
给定一个
n个元素有序的(升序)整型数组nums和一个目标值target,写一个函数搜索nums中的target,如果目标值存在返回下标,否则返回-1。
错解: (未使用二分法)
var search = function(nums, target) {for(let i = 0; i<nums.length;i++){if(nums[i]==target){return i;}}return -1;
};正解:
- 二分法:
- 这道题目的前提是数组为有序数组,同时题目还强调数组中无重复元素,因为一旦有重复元素,使用二分查找法返回的元素下标可能不是唯一的,这些都是使用二分法的前提条件 。
- 对于位移法和防溢出的理解:
right - left:计算两个数的差值。(right - left) >> 1:将差值的二进制表示向右移动一位。这相当于将差值除以2,但因为是位操作,所以通常比整数除法更快。left + ((right - left) >> 1):将上述得到的结果加到left上,得到中间值mid。为什么要这样做而不是直接使用
(left + right) / 2呢?当
left和right都是大整数时,left + right可能会导致整数溢出。例如,在32位整数系统中,如果left是INT_MAX(即最大的32位整数),而right是一个大于零的正数,那么left + right就会溢出。而使用位操作可以避免这种情况,因为right - left的结果一定是小于或等于right的,因此向右移动一位(即除以2)后再加上left就不会溢出。
左闭右闭:
- while (left <= right) 要使用 <= ,因为left == right是有意义的,所以使用 <=
- if (nums[middle] > target) right 要赋值为 middle - 1,因为当前这个nums[middle]一定不是target,那么接下来要查找的左区间结束下标位置就是 middle - 1
/*** @param {number[]} nums* @param {number} target* @return {number}*/
var search = function(nums, target) {// 左闭右闭let mid,left=0,right=nums.length-1;//right是数组最后一个数的下标, 要加等号是因为,左闭右闭,当l=r时,也包含在寻找的区间while(left<=right){// // 位运算 + 防止大数溢出mid=left+((right-left)>>1);// 如果mid所在的数大于目标数,就到左边找,所以right要变if(nums[mid]>target){right=mid-1;// 如果mid所在的数小于目标数,就到右边找,所以left改变}else if(nums[mid]<target){left=mid+1;// 如果刚好等于,就返回mid中位数}else{return mid;}}return -1;
};左闭右开:
- while (left < right),这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle,因为当前nums[middle]不等于target,去左区间继续寻找,而寻找区间是左闭右开区间,所以right更新为middle,即:下一个查询区间不会去比较nums[middle]
/*** @param {number[]} nums* @param {number} target* @return {number}*/
var search = function(nums, target) {// 左闭右开let mid,left=0,right=nums.length;//right是数组最后一个数的下标+1, 不加等号是因为,nums[right]不在查找范围内while(left<right){// // 位运算 + 防止大数溢出mid=left+((right-left)>>1);// 如果mid所在的数大于目标数,就到左边找,所以right要变if(nums[mid]>target){right=mid;// 如果mid所在的数小于目标数,就到右边找,所以left改变}else if(nums[mid]<target){left=mid+1;// 如果刚好等于,就返回mid中位数}else{return mid;}}return -1;
};三、 移除元素(快慢指针法)
题目:. - 力扣(LeetCode)
给你一个数组
nums和一个值val,你需要 原地 移除所有数值等于val的元素,并返回移除后数组的新长度。不要使用额外的数组空间,你必须仅使用
O(1)额外空间并 原地 修改输入数组。元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
正确:
- 数组里面的元素在内存地址中是连续的,是不能删除的,所以要覆盖等于val的值
- 双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
- 快指针:寻找新数组的元素 ,新数组就是不含有目标元素的数组
- 慢指针:指向更新 新数组下标的位置
/*** @param {number[]} nums* @param {number} val* @return {number}*/
var removeElement = function (nums, val) {// 慢指针let i = 0;// 快指针for (j = 0; j < nums.length; j++) {// 如果快指针不等于val,就把不等于val的值给i,实现覆盖等于val的值if (nums[j] != val) {nums[i] = nums[j];// 覆盖一次,i加1,最后覆盖的次数就是数组的新长度。i++;}}return i;
};四、有序数组的平方(双指针法)
题目:. - 力扣(LeetCode)
给你一个按 非递减顺序 排序的整数数组
nums,返回 每个数字的平方 组成的新数组,要求也按 非递减顺序 排序。
正解:
- 双指针法:
我们可以从数组的两端向中间遍历,同时比较两端的元素平方后的大小,并将较大的那个平方值添加到结果数组的开头(因为我们是从后向前添加到结果数组的,以保持顺序)。
- 在JavaScript中,
Array.prototype.unshift()是一个数组方法,用于在数组的开头添加一个或多个元素,并返回新的数组长度。但是,它实际上会修改原始数组,并在其开头添加元素。在您给出的代码示例中:
result.unshift(leftSquare);会在result数组的开头添加leftSquare的值。result.unshift(rightSquare);会在result数组的开头添加rightSquare的值。
/*** @param {number[]} nums* @return {number[]}*/
var sortedSquares = function(nums) {const result = [];// 新数组存放// left指向开头的指针,right指向数组末尾的指针let left = 0, right=nums.length-1;// 从两端开始同时计算平方并比较while(left<=right){const lefts = Math.pow(nums[left], 2);const rights = Math.pow(nums[right], 2);// 将较大的平方值添加到结果数组的开头// 如果lefts大于rights,就把lefts放到新数组最前面if(lefts>rights){result.unshift(lefts);left++}else{// 反之,就把rights放到新数组最前面result.unshift(rights);right--;}}return result;
};五、长度最小的子数组 (滑动窗口)
. - 力扣(LeetCode)
给定一个含有
n个正整数的数组和一个正整数target。找出该数组中满足其总和大于等于
target的长度最小的 连续子数组
[numsl, numsl+1, ..., numsr-1, numsr],并返回其长度。如果不存在符合条件的子数组,返回0。
正解:
滑动窗口(双指针) :
滑动窗口。
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
var minSubArrayLen = function(target, nums) {// 滑动算法let left = 0; let sum = 0; // 最小长度为无穷大let minLength = Infinity; for (let right = 0; right < nums.length; right++) { sum += nums[right]; // 当窗口内的和大于等于目标值时,移动左指针缩小窗口 while (sum >= target) { minLength = Math.min(minLength, right - left + 1); sum -= nums[left]; left++; } }
// 如果找到了,就返回最小子数组的长度;如果没有找到,就返回 0。
// minLength 等于 Infinity就返回0,不等于就返回minLengthreturn minLength === Infinity ? 0 : minLength;
};六、螺旋矩阵
. - 力扣(LeetCode)
给你一个正整数
n,生成一个包含1到n2所有元素,且元素按顺时针顺序螺旋排列的n x n正方形矩阵matrix。
正解:
初始化矩阵:
首先,需要创建一个大小为 n x n 的矩阵(二维数组),并将所有元素初始化为0或者其他占位符。这个矩阵将用于存放最终的结果。设置边界和填充数字:
确定矩阵的四个边界:上边、下边、左边和右边。开始时,上边是矩阵的第一行,下边是最后一行,左边是第一列,右边是最后一列。同时,设置一个变量来跟踪当前要填充的数字,初始值为1。按顺时针螺旋填充:
按照“上边 → 右边 → 下边 → 左边”的顺序,依次填充数字。每次填充完一个边后,调整相应的边界,并继续填充下一个边,直到所有格子都被填满。
- 填充上边:从左到右,填充上边的每个格子,并将上边界下移一行。
- 填充右边:从上到下,填充右边的每个格子,并将右边界左移一列。
- 填充下边:在确保下边还有未填充的格子后,从右到左填充下边的每个格子,并将下边界上移一行。
- 填充左边:在确保左边还有未填充的格子后,从下到上填充左边的每个格子,并将左边界右移一列。
重复填充过程:
重复步骤3,直到所有的格子都被填满,即当前填充的数字达到 n^2 + 1(因为我们是从1开始填充的,所以当数字大于 n^2 时,说明所有格子已经填满)。返回结果:
当所有格子都填满后,返回填充好的矩阵。这种解题思路的关键在于如何正确地更新边界,并在填充过程中保持顺时针螺旋的顺序。通过不断地缩小边界范围,并依次填充每个边界上的格子,最终可以得到所需的矩阵。
/*** @param {number} n* @return {number[][]}*/
var generateMatrix = function(n) {// 初始化一个 n x n 的二维数组(矩阵),并用 0 填充所有元素 let matrix = Array(n).fill(0).map(() => Array(n).fill(0)); // 初始化要填充的数字为 1 let num = 1; // 定义矩阵的四个边界:上、下、左、右 let rowStart = 0, rowEnd = n - 1, colStart = 0, colEnd = n - 1; // 当要填充的数字小于等于 n^2 时,继续填充 while (num <= n * n) { // 从左到右填充上边界(横向) for (let j = colStart; j <= colEnd; j++) { matrix[rowStart][j] = num++; } // 上边界填充完毕后,上边界下移一行 rowStart++; // 从上到下填充右边界(纵向) for (let i = rowStart; i <= rowEnd; i++) { matrix[i][colEnd] = num++; } // 右边界填充完毕后,右边界左移一列 colEnd--; // 从右到左填充下边界(如果还存在未填充的元素) for (let j = colEnd; j >= colStart; j--) { matrix[rowEnd][j] = num++; } // 下边界填充完毕后,下边界上移一行 rowEnd--; // 从下到上填充左边界(如果还存在未填充的元素) for (let i = rowEnd; i >= rowStart; i--) { matrix[i][colStart] = num++; } // 左边界填充完毕后,左边界右移一列 colStart++; } // 返回填充好的矩阵 return matrix;
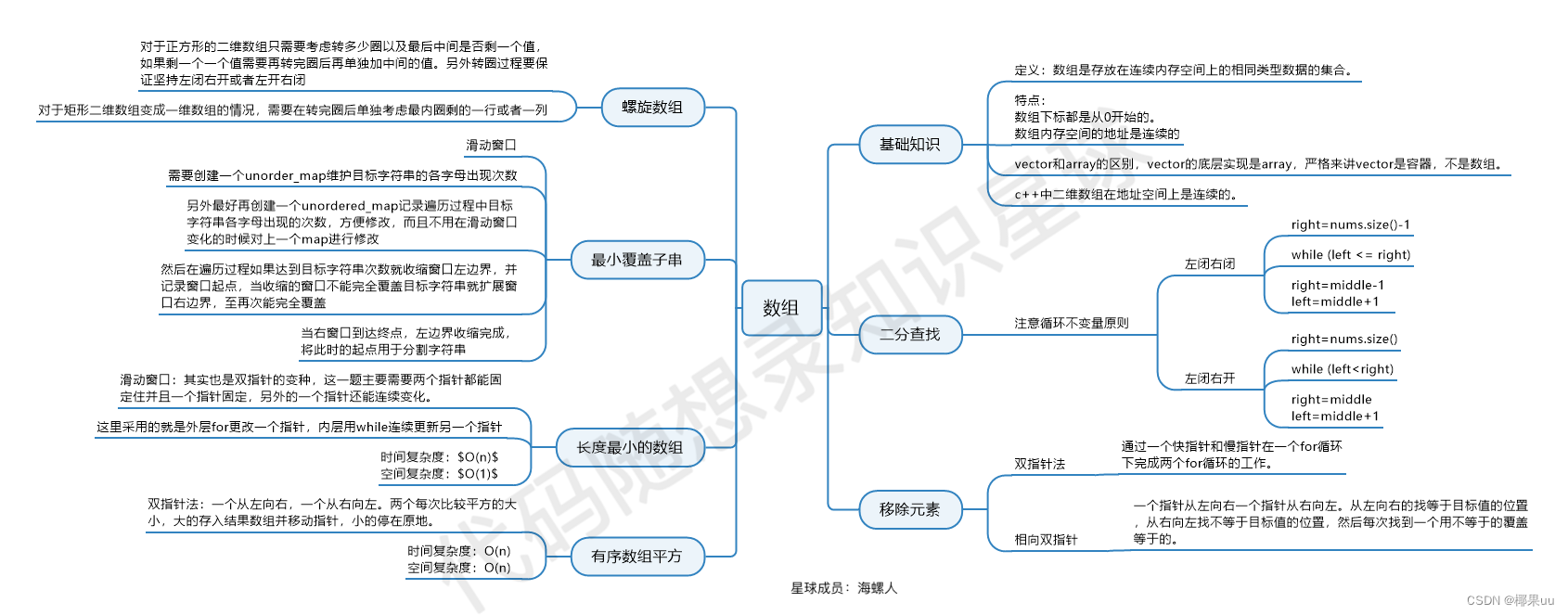
};七、总结



![【C语言】路漫漫其修远兮,深入[指针]正当下](https://img-blog.csdnimg.cn/direct/cf2d2f9ff0d64f81893671aadc8cb46a.gif)