文章目录
- 1.1 目标
- 2 问题陈述
- 2.1 包含我们示例的矩阵 X
- 2.2 参数向量 w \mathbf{w} w 和 b b b
- 3 使用多个变量进行模型预测
- 3.1 逐元素单独预测
- 3.2 单一预测,向量
- 4 使用多个变量计算成本
- 5 使用多个变量的梯度下降
- 5.1 使用多个变量计算梯度
- 多个变量的梯度下降
- 小结
在这个实验中,你将扩展数据结构和之前开发的程序,以 支持多个特征。一些程序已经更新,使得实验看起来很长,但它只是对之前的程序进行了轻微调整,使得复习起来很快。
1.1 目标
- 扩展我们的回归模型程序,支持多个特征
- 扩展数据结构,以支持多个特征
- 重写预测、成本和梯度程序,以支持多个特征
- 利用NumPy np.dot 来向量化它们的实现,以提高速度和简化操作
import copy, math
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
np.set_printoptions(precision=2) # reduced display precision on numpy arrays
-
解释一下:
np.set_printoptions(precision=2)这段代码设置了NumPy打印数组时的选项,其中precision参数设置了打印浮点数时的精度。在这里,precision=2表示浮点数将被打印为小数点后保留两位的形式。
2 问题陈述
您将使用房价预测的示例。训练数据集包含三个示例,具有四个特征(大小、卧室数、楼层数和房龄),如下表所示。请注意,与之前的实验室不同,此处的大小以平方英尺而不是1000平方英尺为单位。这会导致一个问题,您将在下一个实验室中解决!
| 大小(平方英尺) | 卧室数量 | 楼层数 | 房龄(年) | 价格(1000美元) |
|---|---|---|---|---|
| 2104 | 5 | 1 | 45 | 460 |
| 1416 | 3 | 2 | 40 | 232 |
| 852 | 2 | 1 | 35 | 178 |
您将使用这些值构建一个线性回归模型,以便然后可以预测其他房屋的价格。例如,一个面积为1200平方英尺,有3间卧室,1层楼,40年历史的房子。
请运行以下代码单元格以创建您的x_train和y_train变量。
X_train = np.array([[2104, 5, 1, 45], [1416, 3, 2, 40], [852, 2, 1, 35]])
y_train = np.array([460, 232, 178])
2.1 包含我们示例的矩阵 X
与上面的表类似,示例存储在一个 NumPy 矩阵 X_train 中。矩阵的每一行表示一个示例。当您有 m m m 个训练示例(在我们的示例中为三个)和 n n n 个特征(在我们的示例中为四个)时, X \mathbf{X} X 是一个维度为 ( m , n ) (m,n) (m,n) 的矩阵(m 行,n 列)。
X = ( x 0 ( 0 ) x 1 ( 0 ) ⋯ x n − 1 ( 0 ) x 0 ( 1 ) x 1 ( 1 ) ⋯ x n − 1 ( 1 ) ⋯ x 0 ( m − 1 ) x 1 ( m − 1 ) ⋯ x n − 1 ( m − 1 ) ) \mathbf{X} = \begin{pmatrix} x^{(0)}_0 & x^{(0)}_1 & \cdots & x^{(0)}_{n-1} \\ x^{(1)}_0 & x^{(1)}_1 & \cdots & x^{(1)}_{n-1} \\ \cdots \\ x^{(m-1)}_0 & x^{(m-1)}_1 & \cdots & x^{(m-1)}_{n-1} \end{pmatrix} X= x0(0)x0(1)⋯x0(m−1)x1(0)x1(1)x1(m−1)⋯⋯⋯xn−1(0)xn−1(1)xn−1(m−1)
符号说明:
- x ( i ) \mathbf{x}^{(i)} x(i) 是包含示例 i 的向量。 x ( i ) \mathbf{x}^{(i)} x(i) = ( x 0 ( i ) , x 1 ( i ) , ⋯ , x n − 1 ( i ) ) = (x^{(i)}_0, x^{(i)}_1, \cdots,x^{(i)}_{n-1}) =(x0(i),x1(i),⋯,xn−1(i))
- x j ( i ) x^{(i)}_j xj(i) 是示例 i i i 中的第 j j j 个元素。括号中的上标表示示例编号,而下标表示元素。
显示输入数据。
# data is stored in numpy array/matrix
print(f"X Shape: {X_train.shape}, X Type:{type(X_train)})")
print(X_train)
print(f"y Shape: {y_train.shape}, y Type:{type(y_train)})")
print(y_train)#print
X Shape: (3, 4), X Type:<class 'numpy.ndarray'>)
[[2104 5 1 45][1416 3 2 40][ 852 2 1 35]]
y Shape: (3,), y Type:<class 'numpy.ndarray'>)
[460 232 178]
2.2 参数向量 w \mathbf{w} w 和 b b b
-
w \mathbf{w} w 是一个包含 n n n 个元素的向量。
-
每个元素包含与一个特征相关联的参数。
-
在我们的数据集中, n n n 是 4。
-
符号上,我们将其绘制为列向量
w = ( w 0 w 1 ⋯ w n − 1 ) \mathbf{w} = \begin{pmatrix} w_0 \\ w_1 \\ \cdots\\ w_{n-1} \end{pmatrix} w= w0w1⋯wn−1
-
-
b b b 是一个标量参数。
b_init = 785.1811367994083
w_init = np.array([ 0.39133535, 18.75376741, -53.36032453, -26.42131618])
print(f"w_init shape: {w_init.shape}, b_init type: {type(b_init)}")#print
w_init shape: (4,), b_init type: <class 'float'>
3 使用多个变量进行模型预测
模型使用多个变量进行预测的线性模型如下所示:
f w , b ( x ) = w 0 x 0 + w 1 x 1 + . . . + w n − 1 x n − 1 + b (1) f_{\mathbf{w},b}(\mathbf{x}) = w_0x_0 + w_1x_1 +... + w_{n-1}x_{n-1} + b \tag{1} fw,b(x)=w0x0+w1x1+...+wn−1xn−1+b(1)
或者使用向量表示:
f w , b ( x ) = w ⋅ x + b (2) f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w} \cdot \mathbf{x} + b \tag{2} fw,b(x)=w⋅x+b(2)
其中 ⋅ \cdot ⋅ 表示向量的点乘。
为了演示点乘,我们将使用 (1) 和 (2) 实现预测。
3.1 逐元素单独预测
我们先前的预测是将一个特征值乘以一个参数,然后加上一个偏差参数。对于多个特征的预测,直接扩展我们先前的预测实现是使用循环遍历每个元素,执行乘以其参数的操作,然后在末尾加上偏差参数。
def predict_single_loop(x, w, b): n = x.shape[0] # 得到特征值的个数p = 0for i in range(n):p_i = x[i] * w[i] p = p + p_i p = p + b return p
x_vec = X_train[0,:]
print(f"x_vec shape {x_vec.shape}, x_vec value: {x_vec}")# make a prediction
f_wb = predict_single_loop(x_vec, w_init, b_init)
print(f"f_wb shape {f_wb.shape}, prediction: {f_wb}")#print
x_vec shape (4,), x_vec value: [2104 5 1 45]
f_wb shape (), prediction: 459.9999976194083
-
解释一下:
x_vec = X_train[0,:]x_vec = X_train[0,:]这行代码表示从训练数据集X_train中提取第一个样本,即第一行,以向量的形式存储在变量x_vec中。
x_vec 的形状是 (4,),表示一个包含 4 个元素的 1-D NumPy 向量。而结果 f_wb 是一个标量。
3.2 单一预测,向量
注意到上述的方程 (1) 可以使用向量点乘来实现,就像 (2) 中那样。我们可以利用向量运算来加速预测。
回想一下在 Python/Numpy 实验中,NumPy 的 np.dot() 函数可以用来执行向量点乘。
def predict(x, w, b): p = np.dot(x, w) + b return p
# get a row from our training data
x_vec = X_train[0,:]
print(f"x_vec shape {x_vec.shape}, x_vec value: {x_vec}")# make a prediction
f_wb = predict(x_vec,w_init, b_init)
print(f"f_wb shape {f_wb.shape}, prediction: {f_wb}")#print
x_vec shape (4,), x_vec value: [2104 5 1 45]
f_wb shape (), prediction: 459.9999976194083
结果和形状与之前使用循环的版本相同。在接下来的操作中,将使用 np.dot。预测现在是一个单独的语句。大多数例程将直接实现它,而不是调用单独的预测例程。
4 使用多个变量计算成本
具有多个变量的代价函数的方程为:
J ( w , b ) = 1 2 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) 2 (3) J(\mathbf{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 \tag{3} J(w,b)=2m1i=0∑m−1(fw,b(x(i))−y(i))2(3)
其中:
f w , b ( x ( i ) ) = w ⋅ x ( i ) + b (4) f_{\mathbf{w},b}(\mathbf{x}^{(i)}) = \mathbf{w} \cdot \mathbf{x}^{(i)} + b \tag{4} fw,b(x(i))=w⋅x(i)+b(4)
与之前的实验室不同, w \mathbf{w} w 和 x ( i ) \mathbf{x}^{(i)} x(i)现在是向量,而不是标量,支持多个特征。
def compute_cost(X, y, w, b): m = X.shape[0] # 样本的个数cost = 0.0for i in range(m): f_wb_i = np.dot(X[i], w) + b #(n,)(n,) = scalar (see np.dot)cost = cost + (f_wb_i - y[i])**2 #scalarcost = cost / (2 * m) #scalar return cost
# Compute and display cost using our pre-chosen optimal parameters.
cost = compute_cost(X_train, y_train, w_init, b_init)
print(f'Cost at optimal w : {cost}')#print
Cost at optimal w : 1.5578904428966628e-12
5 使用多个变量的梯度下降
多个变量的梯度下降算法如下:
重复 直到收敛: { w j = w j − α ∂ J ( w , b ) ∂ w j 对于 j = 0..n-1 b = b − α ∂ J ( w , b ) ∂ b } \begin{align*} \text{重复}&\text{直到收敛:} \; \lbrace \newline\; & w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} \tag{5} \; & \text{对于 j = 0..n-1}\newline &b\ \ = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline \rbrace \end{align*} 重复}直到收敛:{wj=wj−α∂wj∂J(w,b)b =b−α∂b∂J(w,b)对于 j = 0..n-1(5)
其中, n n n 是特征数量,参数 w j w_j wj, b b b 同时更新,其中
∂ J ( w , b ) ∂ w j = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x j ( i ) ∂ J ( w , b ) ∂ b = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) \begin{align} \frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} \tag{6} \\ \frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \tag{7} \end{align} ∂wj∂J(w,b)∂b∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))xj(i)=m1i=0∑m−1(fw,b(x(i))−y(i))(6)(7)
- m m m 是数据集中的训练示例数量
- f w , b ( x ( i ) ) f_{\mathbf{w},b}(\mathbf{x}^{(i)}) fw,b(x(i))是模型的预测值,而 y ( i ) y^{(i)} y(i) 是目标值
5.1 使用多个变量计算梯度
下面是计算方程(6)和(7)的实现。有许多方法可以实现这个。在这个版本中,有一个
- 外循环遍历所有m个示例。
- 可以直接计算示例的 ∂ J ( w , b ) ∂ b \frac{\partial J(\mathbf{w},b)}{\partial b} ∂b∂J(w,b) 并累积
- 在第二个循环中遍历所有n个特征:
- 分别为每个 w j w_j wj 计算 ∂ J ( w , b ) ∂ w j \frac{\partial J(\mathbf{w},b)}{\partial w_j} ∂wj∂J(w,b)。
def compute_gradient(X, y, w, b): m,n = X.shape #(number of examples, number of features)dj_dw = np.zeros((n,))dj_db = 0.for i in range(m): err = (np.dot(X[i], w) + b) - y[i] for j in range(n): dj_dw[j] = dj_dw[j] + err * X[i, j] dj_db = dj_db + err dj_dw = dj_dw / m dj_db = dj_db / m return dj_db, dj_dw
-
解释一下:
dj_dw = np.zeros((n,))这行代码创建了一个大小为
(n,)的全零数组,其中 n 是特征的数量。这个数组用于存储每个特征对应的梯度值,初始时全部为零。
#Compute and display gradient
tmp_dj_db, tmp_dj_dw = compute_gradient(X_train, y_train, w_init, b_init)
print(f'dj_db at initial w,b: {tmp_dj_db}')
print(f'dj_dw at initial w,b: \n {tmp_dj_dw}')#print
dj_db at initial w,b: -1.6739251501955248e-06
dj_dw at initial w,b:
[-2.73e-03 -6.27e-06 -2.22e-06 -6.92e-05]
多个变量的梯度下降
下面的例程实现了上面的方程(5)。
def gradient_descent(X, y, w_in, b_in, cost_function, gradient_function, alpha, num_iters): J_history = [] # 用于存储每次迭代后计算得到的代价函数的数值。w = copy.deepcopy(w_in) #avoid modifying global w within functionb = b_infor i in range(num_iters):# Calculate the gradient and update the parametersdj_db,dj_dw = gradient_function(X, y, w, b) ##None# Update Parameters using w, b, alpha and gradientw = w - alpha * dj_dw ##Noneb = b - alpha * dj_db ##None# Save cost J at each iterationif i<100000: # prevent resource exhaustion J_history.append( cost_function(X, y, w, b))# Print cost every at intervals 10 times or as many iterations if < 10if i% math.ceil(num_iters / 10) == 0:print(f"Iteration {i:4d}: Cost {J_history[-1]:8.2f} ")return w, b, J_history #return final w,b and J history for graphing
# initialize parameters
initial_w = np.zeros_like(w_init)
initial_b = 0.# some gradient descent settings
iterations = 1000 # 迭代次数
alpha = 5.0e-7 # 学习率# run gradient descent
w_final, b_final, J_hist = gradient_descent(X_train, y_train, initial_w, initial_b,compute_cost, compute_gradient, alpha, iterations)print(f"b,w found by gradient descent: {b_final:0.2f},{w_final} ")m,_ = X_train.shapefor i in range(m):print(f"prediction: {np.dot(X_train[i], w_final) + b_final:0.2f}, target value: {y_train[i]}")# print
Iteration 0: Cost 2529.46
Iteration 100: Cost 695.99
Iteration 200: Cost 694.92
Iteration 300: Cost 693.86
Iteration 400: Cost 692.81
Iteration 500: Cost 691.77
Iteration 600: Cost 690.73
Iteration 700: Cost 689.71
Iteration 800: Cost 688.70
Iteration 900: Cost 687.69
b,w found by gradient descent: -0.00,[ 0.2 0. -0.01 -0.07]
prediction: 426.19, target value: 460
prediction: 286.17, target value: 232
prediction: 171.47, target value: 178
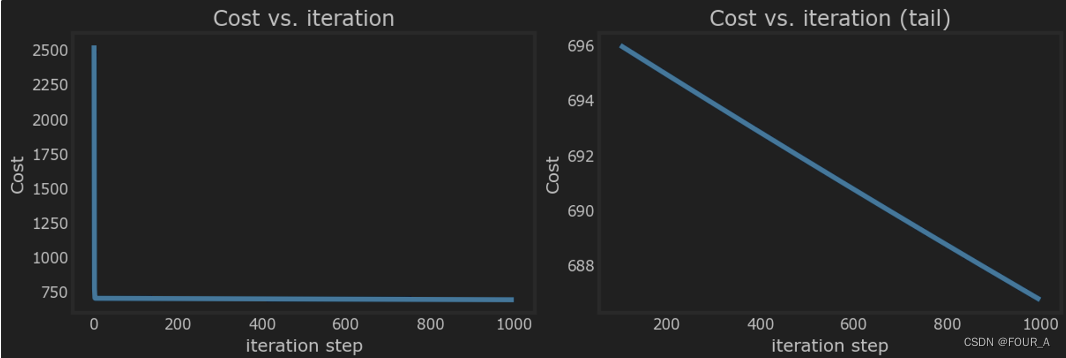
# plot cost versus iteration
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4))
ax1.plot(J_hist)
ax2.plot(100 + np.arange(len(J_hist[100:])), J_hist[100:])
ax1.set_title("Cost vs. iteration"); ax2.set_title("Cost vs. iteration (tail)")
ax1.set_ylabel('Cost') ; ax2.set_ylabel('Cost')
ax1.set_xlabel('iteration step') ; ax2.set_xlabel('iteration step')
plt.show()
-
解释一下:
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4))这行代码使用Matplotlib创建了一个具有两个子图的图形对象。让我来解释一下参数:
fig: 这是整个图形对象的实例。(ax1, ax2): 这是一个包含两个子图对象的元组,分别称为ax1和ax2。您可以在每个子图上绘制数据。plt.subplots(1, 2, constrained_layout=True, figsize=(12, 4)): 这是一个函数调用,用于创建子图。具体地:1, 2表示我们希望创建一个包含1行和2列的子图网格。constrained_layout = True是一个布尔参数,用于启用自动布局调整,以确保子图之间的间距和相对大小是合理的。figsize=(12, 4)指定了图形的尺寸,宽度为12英寸,高度为4英寸。
这行代码将返回一个包含图形对象和子图对象的元组
(fig, (ax1, ax2))。您可以使用ax1和ax2对象分别绘制两个子图中的数据。 -
解释一下:
ax2.plot(100 + np.arange(len(J_hist[100:])), J_hist[100:])这行代码使用
ax2对象绘制损失函数的历史记录,但是仅包含从索引100开始的数据。让我逐步解释:ax2.plot(...): 这是ax2对象的plot方法,用于绘制图形。100 + np.arange(len(J_hist[100:])): 这是 x 轴的值。它是从 100 开始的索引值,直到损失函数历史记录的末尾。np.arange(len(J_hist[100:]))创建一个从 0 开始的索引数组,然后通过添加100来将其偏移。J_hist[100:]: 这是损失函数历史记录的切片,从索引100 开始,一直到末尾。这是 y 轴的值,表示从第100次迭代开始的损失函数值。
小结
在这个实验中:
- 重新开发了多变量线性回归的例程。
- 利用了 NumPy 的
np.dot来向量化实现。