1.引例
一提到查找,我们一上来想的肯定是find()函数或者search()函数,但是这种查找的底层逻辑终究是用顺序查找的方式,运行的时间成本非常高昂,所以平时能不用就不用,比赛的时候用这种查找和自己while遍历,for遍历都是一个样,时间复杂度过高
但是在C++的stl里面有两个十分好用的函数,lower_bound()和upper_bound(),这两个函数的查找逻辑是二分查找,相比于上面的,在时间复杂度上更加小,运行成本更低
2.用法
lower_bound(start,end,value) 用于二分查找区间内第一个 大于等于某值(>= x) 的位置
upper_bound(start,end,value)用于二分查找区间内第一个 大于某值(> x) 的位置
说明一下参数的含义
start:起始迭代器的位置
end:终止迭代器的位置
注意:这些函数的范围,都是左开右闭,也就是说实际的作用范围为[start,end)
value:要查找的值,如果成功,则返回正确的迭代器的位置
但是如果搜遍了整个序列也没有找到合适的值,那么将返回end迭代器的位置
展示
lower_bound
#include<bits/stdc++.h>
using namespace std;int main()
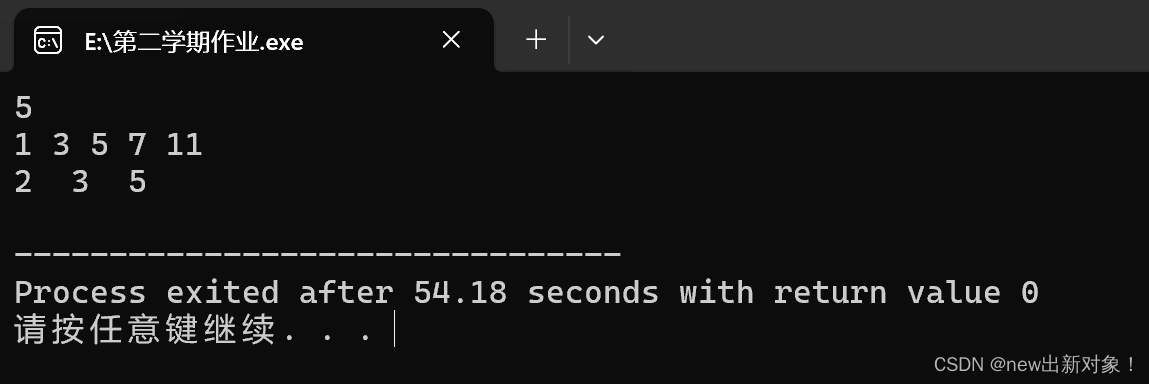
{int n;cin>>n;int a[20];for(int i=1;i<=n;i++){cin>>a[i];}int flag1=lower_bound(a+1,a+n+1,2)-a;int flag2=lower_bound(a+1,a+n+1,5)-a;int flag3=lower_bound(a+1,a+n+1,9)-a;printf("%d %d %d\n",flag1,flag2,flag3);return 0;
}解释:第一个>=2的位置是2,第一个>=5的位置是3,第一个>=9的位置是5
upper_bound
#include<bits/stdc++.h>
using namespace std;int main()
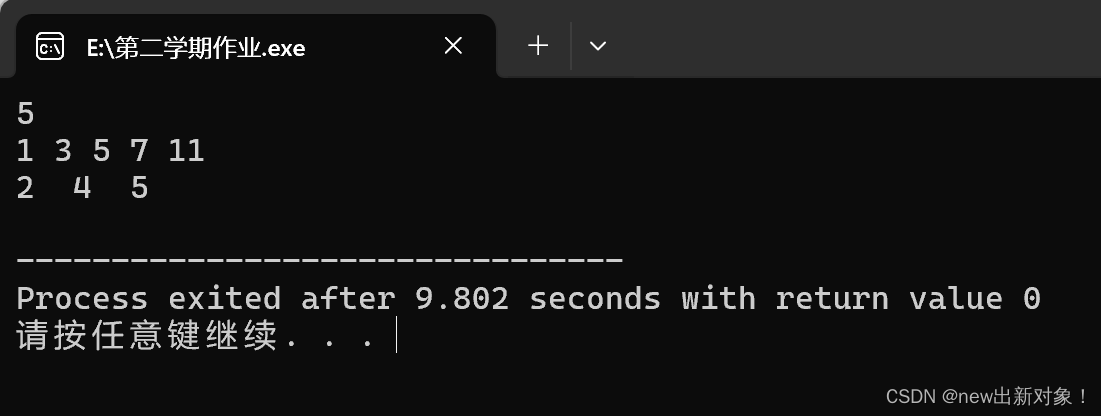
{int n;cin>>n;int a[20];for(int i=1;i<=n;i++){cin>>a[i];}int flag1=upper_bound(a+1,a+n+1,2)-a;int flag2=upper_bound(a+1,a+n+1,5)-a;int flag3=upper_bound(a+1,a+n+1,9)-a;printf("%d %d %d\n",flag1,flag2,flag3);return 0;
}解释:第一个>2的位置是2,第一个>5的位置是4,第一个>9的位置是5
3.例题
这边例题我也就直接甩一个abc比赛上的例题了,因为还算简单,就是重要的是想到二分这个过程
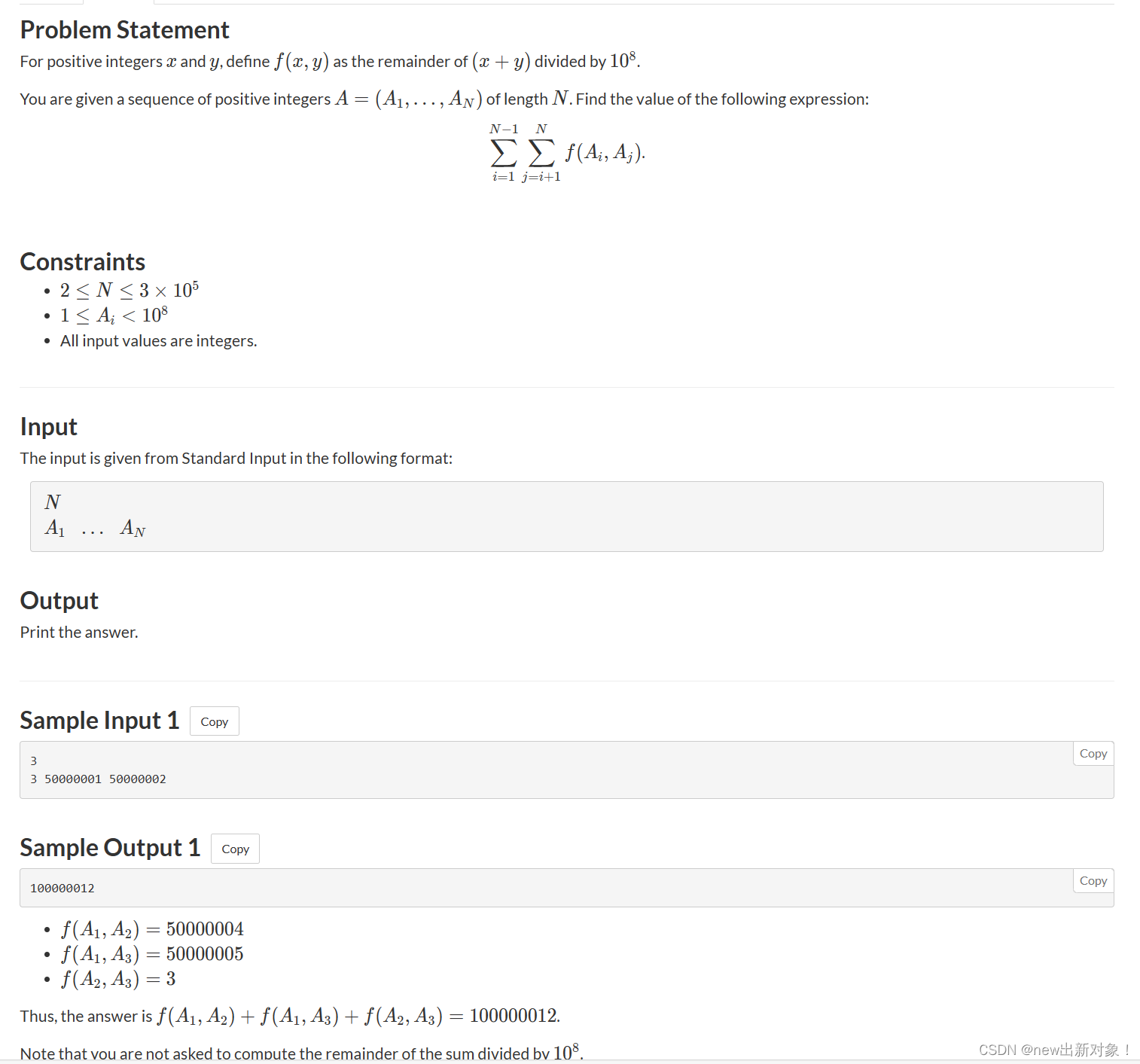
题解:这题就是说有一个数组,每次选取数组里面的两个数去加起来然后取模1e8,这道题一开始我用的暴力,结果直接在第六个数据点就开始时间超限了,后续我想到了用数学思维去解决这道题目,因为我们每次都是两个数加起来,不会大于2e8因此,我们就可以得出一个结论,只要大于1e8就直接减去1e8即可,然后,我们就对这个数组进行排序,然后用lower_bound去查找右边第一个满足两数加起来是 要>=1e8,这样就可以把暴力的O(n^2)的时间复杂度缩短到O(nlogn)的时间复杂度,这样就可以AC这道题了
#include<bits/stdc++.h>
using namespace std;
const long long N=3*1e5+5;
const long long M=1e8;
long long a[N];
long long n;
long long sum=0;
bool cmp(long long fx,long long fy){return fx<fy;
}
int main()
{scanf("%lld",&n);for(long long i=1; i<=n; i++) {scanf("%lld",&a[i]);sum+=a[i]*(n-1);}sort(a+1,a+1+n,cmp);for(long long i=1; i<n; i++) {long long k=lower_bound(a+1+i,a+1+n,M-a[i])-a;sum-=M*(n-k+1);}printf("%lld",sum);return 0;
}


![[Kubernetes] Istio on Kubernetes 实践](https://img-blog.csdnimg.cn/direct/76459f32b4454c2f912b313cd0bd0cde.png)
