Translated from the Scientific American, July/August 2023 issue.

Simply Infinite （简单无限）

New “einstein” tile intrigues the math world.

翻译：新"爱因斯坦"瓷砖引起数学界的兴趣。

Paragraph 1

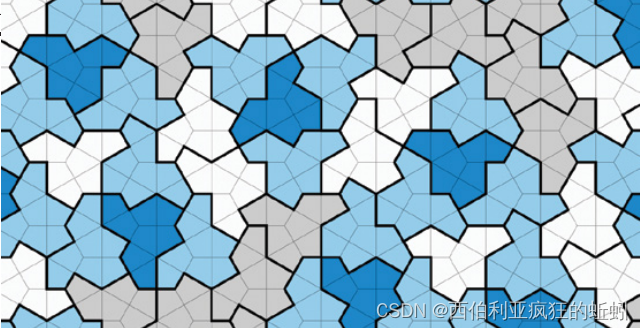
David Smith, a math hobbyist in York-shire, England, has discovered a 13-sided shape that eluded mathematicians for decades.

翻译：David Smith，一个来自英国约克夏的数学业余爱好者，发现了一个令数学家们困惑了数十年的十三边形状。
解释：

• “hobbyist”：业余爱好者
• “eluded”：困惑，迷惑，使不理解
• “decades”：数十年
• David Smith的发现引起了数学界的兴趣，因为这个13边形可能具有独特的性质或特点。

The craggy, hatlike shape is called an “einstein," based on the German for “one stone."

翻译：崎岖的如同帽子一样的形状被称为“爱因斯坦”，源自德语中的“一个石头”的意思。
解释：

• “craggy”：峻峭的、多峭壁的、蜿蜒崎岖的

lf you used einstein-shaped tiles to cover your bathroom floor —— or any flat surface, even if infinitely large —— they would fit together perfectly but never form a repeating pattern.

翻译：如果你使用爱因斯坦形状的瓷砖覆盖你的浴室地板——或者任何平面，即使无限大的平面——他们将完美地拼合在一起，但是绝对不会形成一个重复的图案。
解释：这种特性可能对于一些人来说具有美学或设计上的吸引力，因为它可以创造出独特且不重复的视觉效果。这也可能对数学家和几何学家具有一定的研究价值，因为它涉及到了一种不同于常见重复图案的几何结构。

For decades mathematicians have been hunting for tile shapes like these that can form only nonrepeating arrangements, called aperiodic tilings.

翻译：几十年来，数学家一直在寻找像这样的瓷砖形状，可以形成只有非重复排列的铺砌，被称为"非周期性铺砌"。

• “aperiodic tilings”：非周期性的铺砌，tile 是名词的瓷砖或动词的铺瓷砖，此处用现在分词形式，指的是使用瓷砖铺设的行为或过程。
• 非周期性铺砌对数学和几何学有着重要的研究价值。它们展示了一种独特的排列方式，没有任何部分会在整个铺砌中出现周期性重复。这种特性在数学、物理学、材料科学等领域都有着广泛的应用。非周期性铺砌的研究还涉及到一些复杂的数学理论和算法，包括图论、组合数学和离散几何等领域。

They started with sets of many different tiles: the first set, discovered in 1964, required 20,426 distinct tiles, which was later simplified to 103.

翻译：他们从多种不同的瓷砖集合开始：第一组瓷砖是在1964年发现的，需要20,426块不同的瓷砖，后来简化为103块。
解释：

• “started with”：从…开始
• “set of”：一套的，一系列的
• 这一发现表明，最初的瓷砖集合非常庞大而复杂，由成千上万块不同的瓷砖组成。然而，在进一步的研究和分析中，数学家们成功地找到了一种更简化的瓷砖集合，只需要103块瓷砖就可以实现相同的非周期性铺砌效果。
• 这个发现对于非周期性铺砌的研究具有重大意义。通过减少所需的瓷砖数量，简化了铺砌过程，使得非周期性铺砌更加实用和可行。同时，这也有助于揭示非周期性铺砌的一些普遍规律和原则，为进一步的研究和应用提供了基础。

By 1974 mathematician Roger Penrose had found two tile shapes that, when combined in a mosaic, never formed a repeating pattern.

翻译：在1974年，数学家Roger Penrose已经发现了两种瓷砖形状，当它们在马赛克中拼接时，永远不会形成重复图案。
解释：

• 这个发现对于非周期性铺砌的研究具有重大意义。通过彭罗斯的发现，我们知道至少存在两种瓷砖形状，它们可以被用来创建非重复的铺砌。这表明非周期性铺砌并不是不可能实现的，而是存在具体的瓷砖形状和组合方式。
• 彭罗斯的发现为非周期性铺砌领域的进一步研究和探索提供了重要的基础。这也激发了其他数学家和研究人员的兴趣，进一步推动了非周期性铺砌的发展和应用。

Paragraph 2

But was it possible to form an aperiodic tiling with tiles of only one shape 一 the hypothetical einstein?

翻译：但它是否可能形成一种只用一种形状的瓷砖铺成的非周期性图案，比如假设中的爱因斯坦瓷砖？
解释：

• “was it possible”：可能吗
• “an aperiodic tiling”：一个非周期性的铺砌，即铺出非周期性的图案
• “with tiles (of only one shape)”：用瓷砖（只有一种形状的）
• “hypothetical”：（基于）假设的

Doris Schattschneider, a retired mathematician affiliated with Moravian University with expertise in tessellations, had been skeptical about the likelihood of a true einstein ever being discovered.

翻译：Doris Schattschneider，一个退休的数学家，在镶嵌领域的专业知识上与Moravian大学有合作，她一直对真正的爱因斯坦铺砌被发现的可能性持怀疑态度。
解释：

• " a retired mathematician"：一个退休的数学家
• “affiliated with”：表明个人或实体与某个组织有一定的合作关系或从属关系，但并不一定是该组织的正式成员或雇员。这种关联可能是基于合作项目、研究合作、学术交流或其他形式的合作关系。
• “expertise in tessellations”：镶嵌方面的专业知识
• “skeptical”：持怀疑态度的
• 这句话暗示了这个问题在学术界中可能存在一定的争议。

“That’s why it was so startling that not only was this found, but it’s such a simple tile," she says. “To me, it’s a total anomaly.”

翻译：“这就是为什么发现它如此令人震惊的原因，不仅因为它被发现了，而且因为这是一个如此简单的瓷砖，”她说。“对我来说，这完全是一个异常。”
解释：

• “total anomaly”：总的异常
• 总的来说她表达的是这个发现是令人震惊的，因为在此之前，人们认为只有复杂的瓷砖形状才能创建非周期性的铺砌。因此，这种简单的瓷砖被视为一个异常，因为它打破了人们对非周期性铺砌的常规理解。

The tile Smith discovered in November 2022, while he was experimenting with different shapes using a software called PolyForm Puzzle Solver, was astonishing in its elegance.

翻译：Smith 在2022年11月发现了该瓷砖，当他正在用一款叫做PolyForm Puzzle Solver的软件试验不同的形状时，这个瓷砖的优雅之处令人震惊。
解释：

• “was experimenting with different shapes”：正在试验不同的形状（过去）
• “was astonishing in its elegance”：注意这句话前面是逗号，而且本身缺少主语，所以再往前追溯到第一个逗号，说明两个逗号之间是补充性的文本，可以忽略并连接逗号两端形成一个完整的句子。那么was的主语就变成了the tile （Smith discovered in November 2022）。
• “astonishing”：ing的后缀一般表示的形容词带有，“令人…的”，此处可以理解为令人惊讶/震惊的。
• 句子的目的是描述这个发现的令人惊叹之处以及瓷砖的优雅性。它突出了这个发现的重要性和独特性，以及对发现者史密斯的赞赏和惊叹。

Made up of right-angled kites, it was nothing like the gnarly, complicated kind of shape many mathematicians would have predicted.

翻译：这与许多数学家可能预测的独特、复杂形状完全不同，它是由直角风筝的形状组成。
解释：

• “right-angled”：直角
• “gnarly” ：是一个俚语词汇，用于形容某物或某人具有独特、有趣或引人注目的特征或品质。它通常表示某物或某人的外观、状况或表现给人留下了深刻的印象。这个词通常用来形容事物的独特、复杂或错综复杂的性质。
• “it was nothing like”：与…一点都不像
• “the gnarly, complicated kind of shape”：独特、 复杂的形状
• 句子指出了瓷砖的外观与数学家们可能预测的复杂形状截然不同。这可能意味着数学家们可能预测了更复杂、更不规则的形状，而实际发现的瓷砖却是由直角风筝形状组成的，这种简单、对称的形状对于他们来说是出乎意料的。

Paragraph 3

Smith e-mailed Craig Kaplan, a computer scientist at the University of Waterloo in Ontario, who recognized the shape’s potential.

翻译：Smith给Craig Kaplan发了邮件，一位安大略省滑铁卢大学的计算机科学家，他认识到了这种形状的潜力。
解释：句子的目的是说明史密斯主动联系了克雷格·卡普兰，并强调卡普兰对这种形状的认识和意识到其潜力的重要性。这为史密斯进一步探索和研究这种瓷砖的应用提供了一个合作伙伴和专业的视角。

Although the mosaic it created seemed not to have a repeating pattern, the duo needed to mathematically prove it never would —— even if the mosaic were infinitely large.

翻译：虽然它创造的马赛克似乎没有重复图案，但这对组合需要通过数学方法证明，即使马赛克无限大也不会重复。
解释：

• “mosaic”：马赛克
• “seem to”：似乎
• “due”：搭档、一对表演者
• 句子的目的是强调这对组合不仅仅是观察了马赛克的外观，而是需要通过数学证明来确保它的非重复性。

They enlisted software developer Joseph Samuel Myers and University of Arkansas mathematician Chaim Goodman-Strauss, who had both worked with tiling and combinatorics in the past.

翻译：他们聘请了软件工程师Joseph Samuel Myers 和 Arkansas 大学的数学家Chaim Goodman-Strauss，他们以前都曾从事铺砌和组合数学相关工作。
解释：

• “enlist”：征召，聘用
• "software developer "：软件开发者
• "combinatorics "：组合数学、组合学
• “in the past”：过去、曾经
• 这个句子强调了约瑟夫·塞缪尔·迈尔斯和哈伊姆·古德曼-斯特劳斯的专业背景，并暗示了他们在平铺和组合学领域的专长将有助于解决这个问题。

Paragraph 4

The researchers used two methods to prove they had a genuine einstein on their hands.

翻译：研究者们使用两种方法来验证他们手上的是真正的爱因斯坦瓷砖。

First, they showed that the hat-like tiles, when arranged together, formed four specific kinds of shapes.

翻译：首先，他们展示了像帽子一样的瓷砖，当拼在一起的时候，形成了四个特殊的形状。
解释：研究人员通过实验证明了帽状瓷砖的排列方式具有一定的规律性，并且能够形成四种特定的形状。这些形状可能是基于瓷砖的几何属性或者其他特定的规则和要求。通过观察和分析这些形状，研究人员可以得出结论，证明了瓷砖排列形成了特定的形状。

Adding more tiles forms even bigger versions of those same shapes, or “supertiles;” the more tiles added, the bigger the supertiles become.

翻译：增加更多的瓷砖形成了更大号的相同形状，或者“超级瓷砖”，瓷砖加的越多，这个超级瓷砖就越大。
解释：

• “even” 在这里表示程度增强或比较。它强调随着瓷砖数量的增加，超级瓷砖的大小也相应增加，形成更大的版本。它传达了一个连续递增的关系，即更多的瓷砖会导致更大的超级瓷砖。
• 研究人员通过实验和观察发现，当他们不断添加更多的瓷砖时，这些瓷砖会形成更大版本的之前所描述的四种特定形状。这种现象被称为“超级瓷砖”，因为它们是之前形状的更大版本。

Mathematicians have proved that this hierarchical structure means the tiling can’t be split into repeating sections and thus must be aperiodic.

翻译：数学家们证明了这种层次结构意味着这个瓷砖无法分割成重复的部分，因此一定是非周期性的。
解释：

• “hierarchical”：等级制的；等级制度的；按等级划分的
• 数学家通过数学证明和推理，得出了这种瓷砖排列的特性。他们发现，由于瓷砖的层次结构，无法将整个瓷砖排列划分为重复出现的部分。换句话说，无法找到固定的重复模式或周期性的规律。这种情况下，瓷砖排列被认为是“非周期性的”。

For the second proof, the team invented a new method that could compare the hat tilings with the nonperiodic tilings of better-known shapes called polyiamonds.

翻译：对于第二种证明，团队发明了一种新的方法，可以将帽子瓷砖与被称为多菱形的更为常见的非周期性瓷砖进行比较。
解释：

• “nonperiodic”：形容词， 非周期性的，指不具有重复模式或周期性规律的特性或性质。
• “better-known”：形容词短语，更为常见或为人熟知的，指与其他事物相比更为广为人知的。
• “polyiamonds”：名词，多棱形，一种特定的几何形状，具有非周期性。
• 多菱形是一种常见的几何形状，具有非周期性的特征。通过将帽子瓷砖与多菱形进行比较，研究团队可以揭示帽子瓷砖与其他已知非周期性瓷砖之间的相似性和差异性。

In the process, the team also showed that one could make an infinite number of similar einsteins by tweaking some of the sides’ lengths.

翻译：在这个过程中，该团队也证明了通过调整一些边的长度能够产生一个无限数量相似的爱因斯坦图案。
解释：

• “that one” 指的是"an infinite number of similar einsteins"（无限数量相似的爱因斯坦图案）中的一个。
• “tweak”：调整
• 这个发现展示了图案的灵活性和变化性。通过微小的修改，图案可以变得相似但又不完全相同。这种灵活性和变化性使得可以制作出无限数量的相似图案，每个图案都有自己独特的特点。这为设计师、艺术家和数学家等提供了更多的创造性空间和可能性。

Paragraph 5

Even with these proofs, mathematicians haven’t yet formulated a broader theory for what makes this simple hat shape so special.

翻译：尽管有这些证明，数学家们还没有为这个简单的帽子形状制定一个更广泛的理论，解释它为什么如此特殊。
解释：

• “formulate”：制定
• “a broader theory”：一个具有更广泛性的理论
• "for what"引导了一个问题，询问关于这个简单帽子形状为什么特殊的目的或原因。

“This is still very mysterious," says mathematician Rachel Greenfeld of the Institute for Advanced Study in Princeton, N.J.

翻译：“这至今依然是个迷，”来自普林斯顿高级研究院的数学家Rachel Greenfeld说道。

There may be more classes of einstein tiles out there, waiting to be discovered, but the geometric hat isn’t revealing any clues, says Marjorie Senechal, a retired mathematician affiliated with Smith College:“These things you stumble upon.”

翻译：可能存在更多种类的爱因斯坦瓷砖有待发现，但几何形状的帽子并没有揭示任何线索，来自史密斯学院的退休数学家Marjorie Senechal说道：“这些东西是你偶然发现的。”
解释：

• “stumble upon”：偶然发现
• Marjorie Senechal指出，有时候在数学研究中，人们会偶然发现一些新的事物或现象，而不是有意地去寻找它们。她使用了“这些东西是你偶然发现的”这句话来形容这种情况。
• 这表明在爱因斯坦瓷砖的领域中，可能还存在其他未知的瓷砖种类，但目前研究几何帽子并没有提供任何关于这些种类的线索。这也强调了数学研究中的探索性质，有时候需要通过偶然的发现来推动领域的进展。

—— Manon Bischoff and Allison Parshall