稳定性的判断:如果两个相同大小的元素也进行了交换就是不稳定,否则稳定
1.直接插入排序:
当插入第 i 位置元素时,前面 0 到 i-1 位置的元素已经各自有序。
此时将i 再次从i-1到0位置依次进行比较。找到合适位置将其插入,原本位置上的元素后移。
插入排序性质:
1.元素越接近有序,其效率越高。
2.时间复杂度:O(N^2)
3.空间复杂度:O(1) //不占用额外的空间
4.稳定性:稳定 //一般判断是否稳定的标准是 遇到相同的元素是否交换,不交换则稳定
代码实现:
public static void insertSort(int[]array){//i从第二个位置开始遍历for(int i=1;i<array.length;i++){//每次外层循环都将i的值记录下来int temp = array[i];int j = i-1;//j从i的后一个元素开始,依次向后遍历for(;j>=0;j--){if(array[j] > temp){array[j+1] = array[j];}else{如果j的值小于或等于i直接跳出,继续i遍历break;}}array[j+1] = temp;}
}2.希尔排序(缩小增量版排序)
思想:先选定一个整数,把待排序的数据按照这个整数的大小进行分组,
再依次对各个组内的数据进行排序。这个整数不断减小,直到为1时,将所有数据
放在同一组排序。
下图为每次分组排序的过程。当gap=1 时排序完成,依次交换画下线的元素
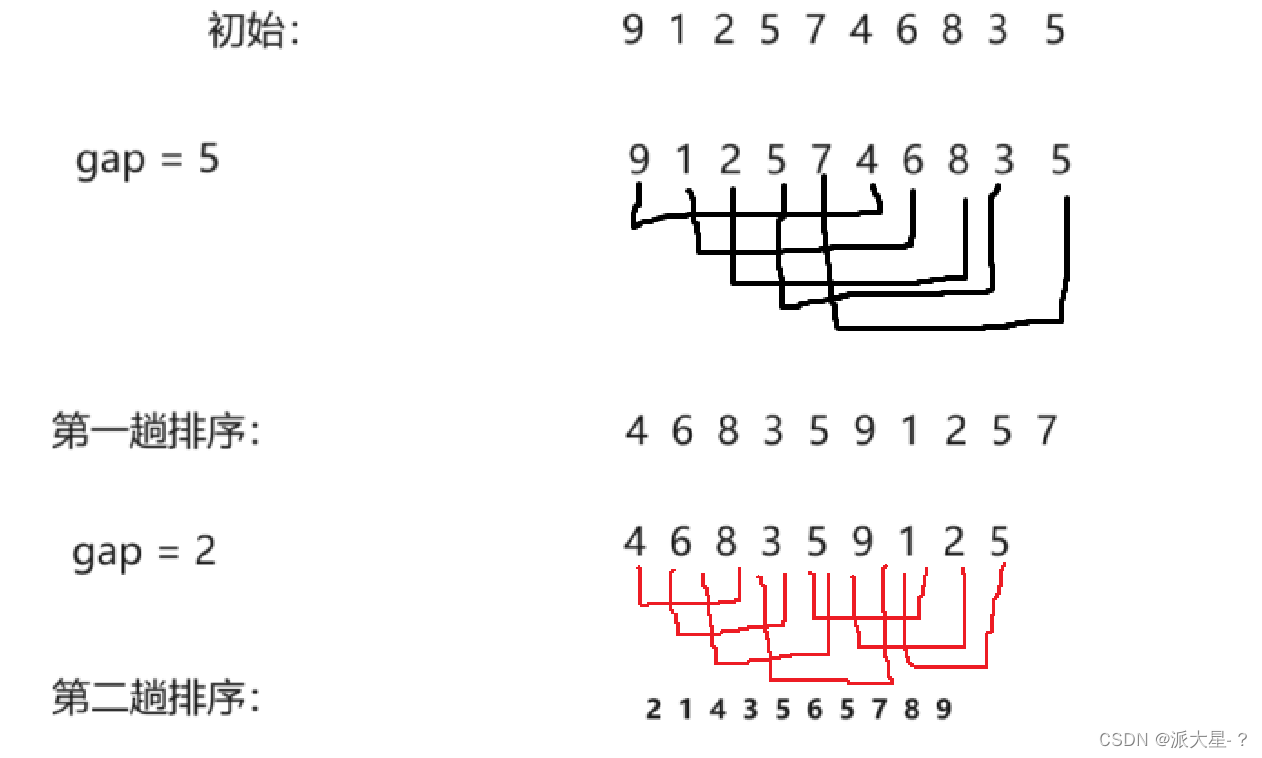
总结:
1.希尔排序是对插入排序的优化,
2.当gap = 1之前,都是对数组的预排序目的是让数组更加接近有序,
对整体而言当gap = 1时可以很好的排序,达到优化效果
3.希尔的时间复杂度不容易计算,因为gap的取值有很多。
大多数的书给出的希尔排序的时间复杂度都不同,一般按照O(n^1.25)到O(6*n^1.25)计算
4.稳定性:不稳定
代码实现:
/*** 希尔排序(分组后 用到插入排序)* 稳定性:不稳定* 时间复杂度:logN* @param arry*/public static void shellSort(int[] arry){//分组 gapint gap = arry.length;while(gap > 1){gap =gap/3+1;shell(arry,gap);}}/*** 每组进行插入排序* @param array* @param gap*/private static void shell(int[] array,int gap){for (int i = gap; i < array.length; i++) {int temp = array[i];int j = i-gap;for(;j>=0;j-=gap){if(array[j] > temp){//将小的赋值给大的array[j+gap] = array[j];}else {break;}}//不小就自己给自己赋值array[j+gap] = temp;}}
3.选择排序
思想:每次从排序的元素中选择最小或者最大的,放在序列的起始位置,直到要排序的元素全部拍完。
缺陷:效率不高,实际很少使用
时间复杂度:O(N^2),最坏情况每个元素两两之间都要比较
空间复杂度:O(1)
稳定性:不稳定
代码如下:
*/public static void swap(int[]array,int i,int j){int temp = array[j];array[j] = array[i];array[i] = temp;}public static void selectSort(int[]array){for(int i=0;i< array.length;i++){int mindex = i;//从第二个位置开始寻找最下值的线标for(int j=i+1;j< array.length;j++){if(array[j]<array[mindex]){mindex = j;}}//找到的最小值下标与当前位置交换swap(array,mindex,i);}}
}
代码二:
4.堆排序(以大根堆为例)
排升序建立大根堆,排降序建立小根堆
时间复杂度:O(n*logn) 每一次的排序为logn,进行n次排序
空间复杂度:O(1) //不占用额外的空间
稳定性:不稳定
/*** 升序建立大根堆*/public static void headSort(int[]array){bigHead(array);int end = array.length-1;while (end>=0){swap(array,0,end);shiftDown(array, end,0 );end--;}}/*** 建立大根堆* @param arr*/public static void bigHead(int[]arr){for (int parent = (arr.length-1-1)/2; parent >=0 ; parent--) {shiftDown(arr,arr.length-1,parent);}}/***向下排序* @param array* @param end* @param parent*/public static void shiftDown(int[]array,int end,int parent){//左子树int child = 2*parent+1;while (child < end){//先判断右节点是否存在if(child+1 <end && array[child+1] >array[child]){child +=1;}if(array[child] > array[parent]){swap(array,child,parent);parent = child;child = 2*parent+1;}else {break;}}}/*** 用来交换数据的函数* @param array* @param i* @param j*/public static void swap(int[]array,int i,int j){int temp = array[j];array[j] = array[i];array[i] = temp;}5.冒泡排序
时间复杂度:O(N^2)
空间复杂度:O(1)
稳定性:稳定
代码实现:
public static void bubbleSort(int[]array){for (int i = 0; i < array.length-1; i++) {//定义flag进行优化,如果一趟下来都没有交换元素,则已经有序//直接break跳出,进行下一趟的比较boolean flag = false;for (int j = 1; j <array.length-i-1 ; j++) {if(array[j] > array[j+1]){swap(array,j,j+1);flag = true;}}//在优化的情况下如果数据 1 2 3 4 5//时间复杂度为:O(N)if(flag == false){break;}}}