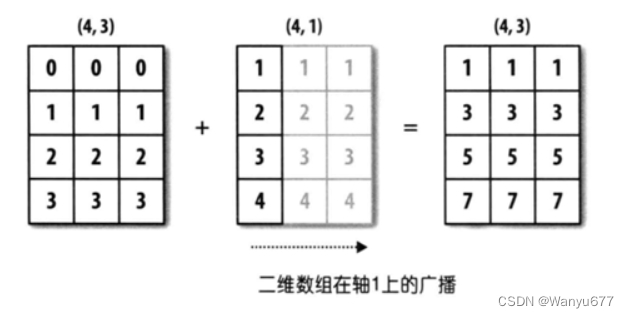
min下面的x称为优化向量或者是决策变量



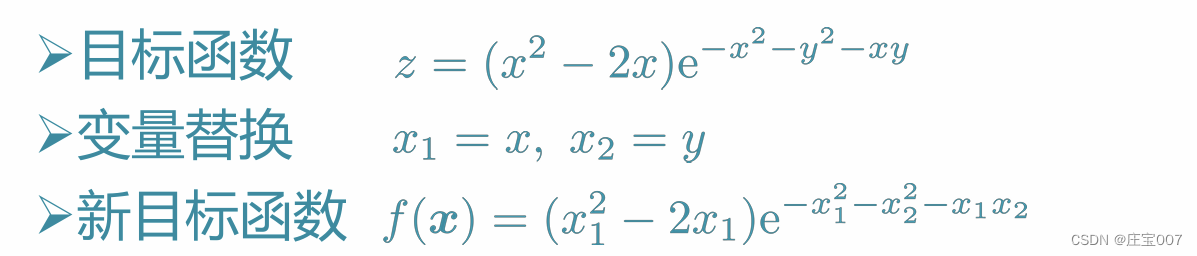
匿名函数法
>> f=@(x)(x(1)^2-2*x(1))*exp(-x(1)^2-x(2)^2-x(1)*x(2)); x0=[0; 0]; [x,b,c,d]=fminsearch(f,x0),
x =
0.6111
-0.3056
b =
-0.6414
c =
1
d =
包含以下字段的 struct:
iterations: 72
funcCount: 137
algorithm: 'Nelder-Mead simplex direct search'
message: '优化已终止:↵ 当前的 x 满足使用 1.000000e-04 的 OPTIONS.TolX 的终止条件,↵F(X) 满足使用 1.000000e-04 的 OPTIONS.TolFun 的收敛条件↵'
使用函数fminunc():
>> [x,b,c,d]=fminunc(f,[0;.0])
Local minimum found.
Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.
<stopping criteria details>
x =
0.6110
-0.3055
b =
-0.6414
c =
1
d =
包含以下字段的 struct:
iterations: 7
funcCount: 27
stepsize: 1.8220e-04
lssteplength: 1
firstorderopt: 1.8030e-06
algorithm: 'quasi-newton'
message: '↵Local minimum found.↵↵Optimization completed because the size of the gradient is less than↵the value of the optimality tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The first-order optimality measure, 6.010135e-07, is less ↵than options.OptimalityTolerance = 1.000000e-06.↵↵'

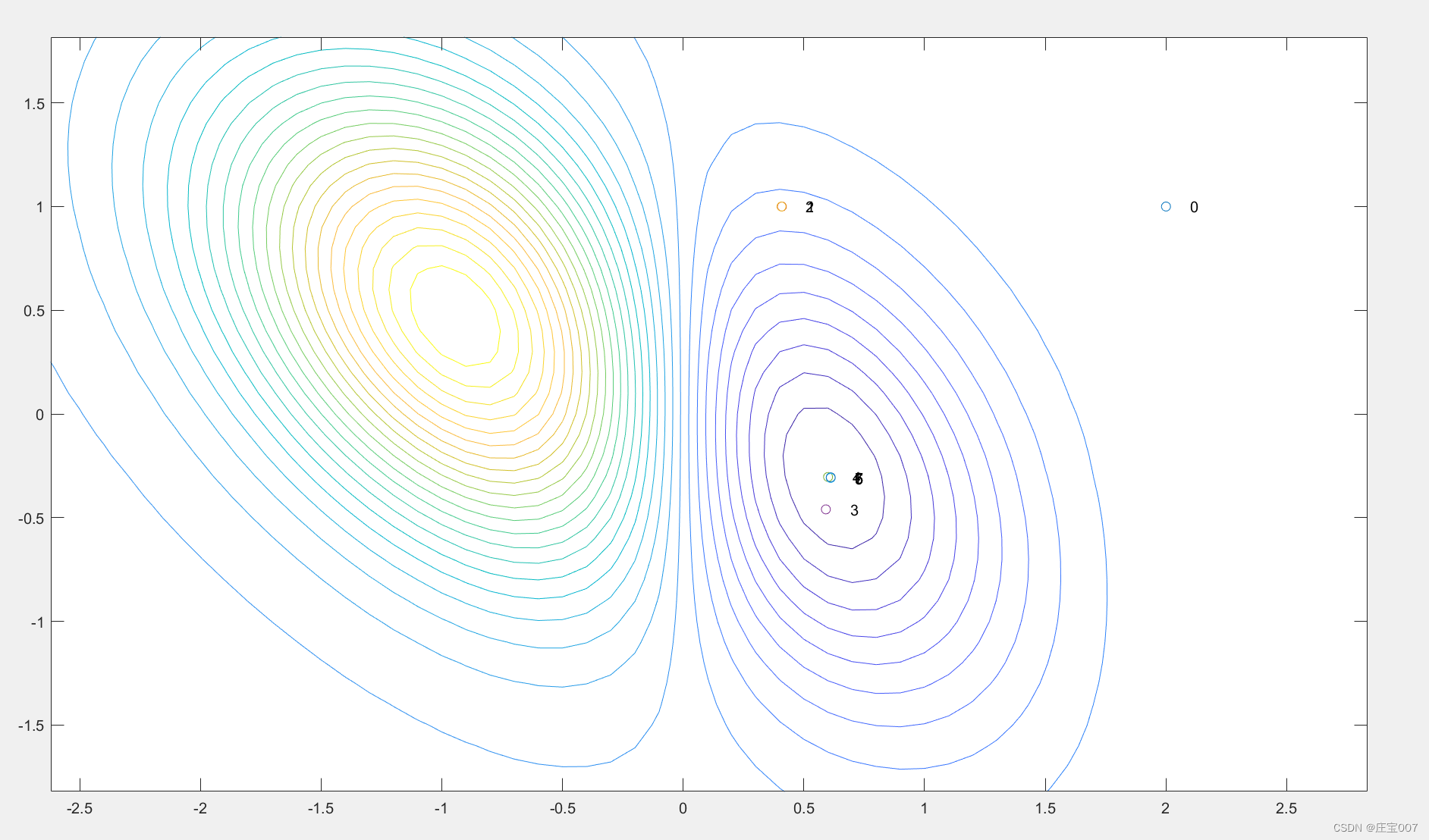
绘制三维等高线 ,获得并叠印中间结果
>> [x,y]=meshgrid(-3:.1:3, -2:.1:2); z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y); contour(x,y,z,30);ff=optimset;
ff.OutputFcn=@myout; x0=[2 1];
x=fminunc(f,x0,ff)Local minimum found.Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.<stopping criteria details>x =0.6110 -0.3055
最优化求解函数的另一种调用方法
建立最优化问题的“结构体”模型
>> problem.solver='fminunc'; problem.options=optimset; problem.objective=@(x)(x(1)^2-2*x(1))*exp(-x(1)^2-x(2)^2-x(1)*x(2)); problem.x0=[2; 1]; [x,b,c,d]=fminunc(problem)Local minimum found.Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.<stopping criteria details>x =0.6110-0.3055b =-0.6414c =1d = 包含以下字段的 struct:iterations: 7funcCount: 66stepsize: 1.7059e-04lssteplength: 1firstorderopt: 7.4506e-09algorithm: 'quasi-newton'message: '↵Local minimum found.↵↵Optimization completed because the size of the gradient is less than↵the value of the optimality tolerance.↵↵<stopping criteria details>↵↵Optimization completed: The first-order optimality measure, 7.437017e-09, is less ↵than options.OptimalityTolerance = 1.000000e-06.↵↵'