14.跳跃游戏Ⅱ-编程知识

14.跳跃游戏Ⅱ

文章目录

题目简介
题目解答
- 解法一：贪心算法+动态规划
- - 代码：
  - 复杂度分析：
题目链接

大家好，我是晓星航。今天为大家带来的是跳跃游戏Ⅱ 相关的讲解！😀

题目简介

在这里插入图片描述

题目解答

解法一：贪心算法+动态规划

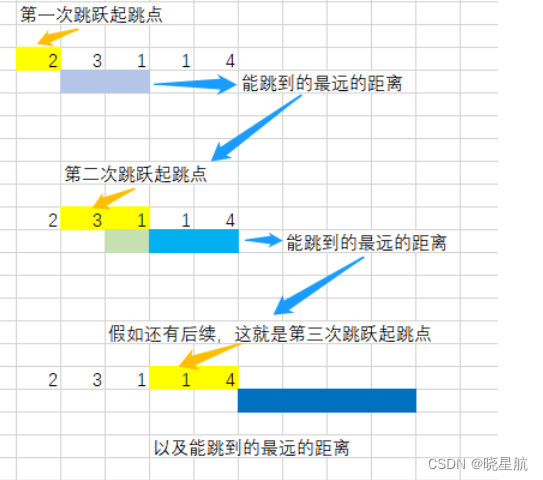
思路：想象你在玩大富翁，回合制游戏，随身带的钱决定你每回合最多可以走多少格，需要以最短的回合数到达终点。格子里面的数字代表“钱”，每回合你需要停留在格子里休息得到补充的“钱”才能继续行走。每次走到一个格子的时候，你需要估计预算在下一个回合能走多少格，哪个格子的钱最多，下一回合就去那个格子。但是前面的格子里有多少钱有战争迷雾看不到，要到了才知道。 border 指本回合能走的最远位置，即钱用完了就不能继续往前了 maxPosition 就是钱
在这里插入图片描述

代码：

class Solution {public int jump(int[] nums) {// 记录当前能跳跃到的位置的边界下标int border = 0;// 记录在边界范围内，能跳跃的最远位置的下标int maxPosition = 0;// 记录所用步数int steps = 0;for(int i=0;i<nums.length-1;i++){// 继续往下遍历，统计边界范围内，哪一格能跳得更远，每走一步就更新一次能跳跃的最远位置下标// 其实就是在统计下一步的最优情况maxPosition = Math.max(maxPosition,nums[i]+i);// 如果到达了边界，那么一定要跳了，下一跳的边界下标就是之前统计的最优情况maxPosition，并且步数加1if(i==border){border = maxPosition;steps++;}}return steps;}
}