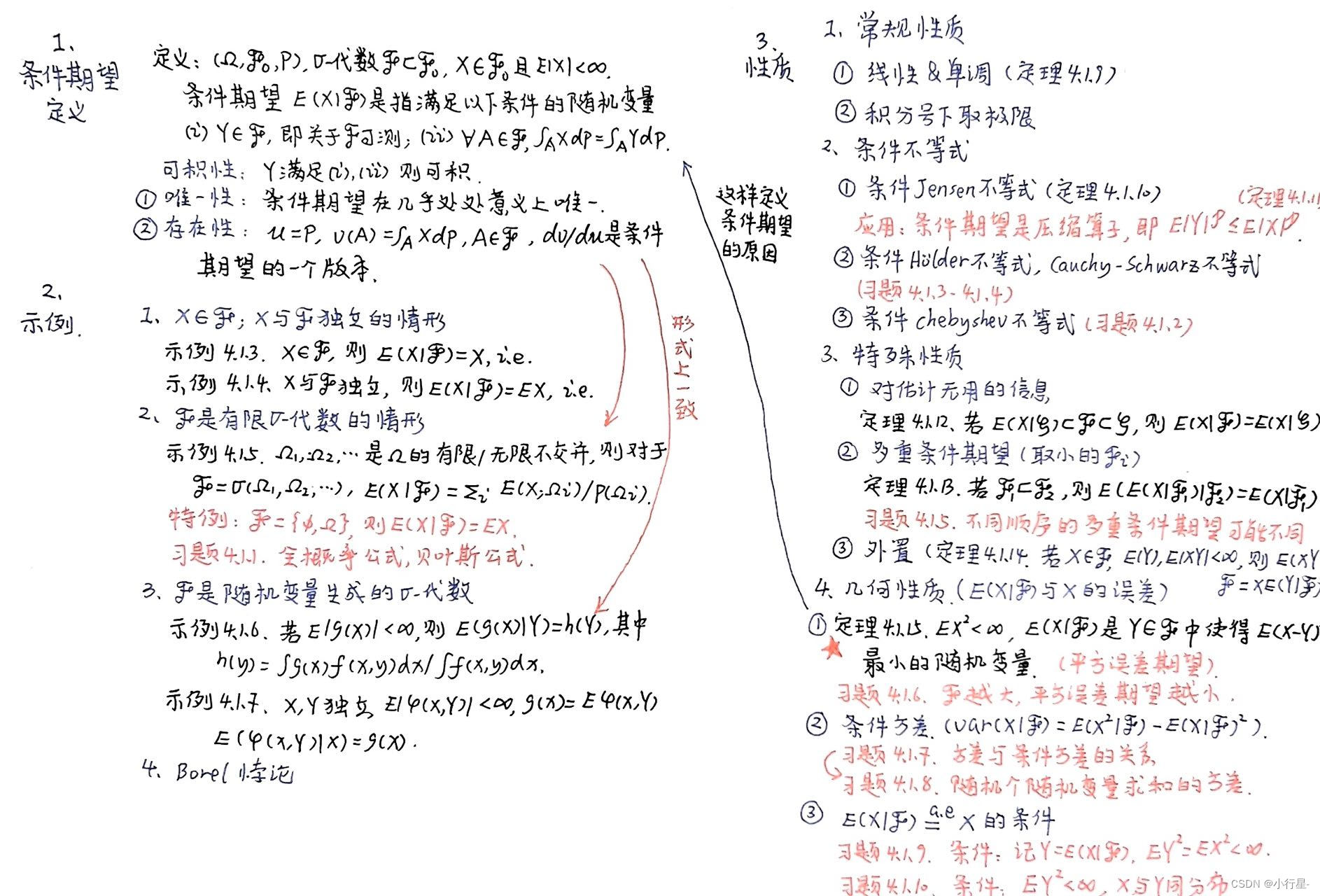
1.1. 离散时间鞅-条件期望
- 条件期望
- 1. 条件期望的定义
- 1.1. 条件期望的定义
- 1.2. 条件期望的存在唯一性
- 2. 条件期望的示例
- 3. 条件期望的性质
- 3.1. 常规性质
- 3.2. 条件不等式
- 3.3. 特殊性质
- 3.4. 几何性质
- 4. 正则条件概率
条件期望
条件期望可以认为是在掌握部分信息 F \mathcal{F} F下对随机变量 X X X的最佳估计, 即对于每一个 A ∈ F A\in \mathcal{F} A∈F,我们知道事件 A A A是否发生, E ( X ∣ F ) E(X|F) E(X∣F)是在所获得信息下对 X X X值的“最佳猜测”(定理4.1.15说明条件期望是与 X X X平均二次误差最小的随机变量). 依据这个概念定义条件期望并且给出条件期望的示例(条件期望在不同 σ \sigma σ代数下的具体表示.)
基于掌握的部分信息 F \mathcal{F} F, 将与 X X X平均二次误差最小的随机变量定义为条件期望, 由此给出了条件期望的定义 第一节 , 对于不同的 F \mathcal{F} F(平凡, 有限 σ \sigma σ代数, 随机变量生成的 σ \sigma σ代数), 条件期望有具体的表示, 这个和本科的条件期望定义联系起来 第二节 .
条件期望有期望的类似性质, 也有独特的性质(重期望, 外置等), 并且具有几何性质, 即 E ( X ∣ F ) E(X|F) E(X∣F)是在所获得信息下对 X X X值的“最佳猜测” 第三节 , 关于随机变量生成的 σ \sigma σ代数的条件期望可以写成条件概率的积分, 最后主要分析可以有这种表示的条件, 即正则条件概率 第四节 .
1. 条件期望的定义
1.1. 条件期望的定义
定义4.1.1.条件期望 给定概率空间 ( Ω , F o , P ) \left(\Omega, \mathcal{F}_{o},P\right) (Ω,Fo,P), σ \sigma σ-代数 F ⊂ F o \mathcal{F} \subset \mathcal{F}_{o} F⊂Fo,随机变量 X ∈ F o X \in \mathcal{F}_{o} X∈Fo满足 E ∣ X ∣ < ∞ E|X|<\infty E∣X∣<∞. 给定 F \mathcal{F} F下 X X X的条件期望 E ( X ∣ F ) E(X \mid \mathcal{F}) E(X∣F) 是满足以下条件的任意随机变量 Y Y Y
( i ) (i) (i) Y ∈ F Y \in \mathcal{F} Y∈F, 即是 F \mathcal{F} F可测;
( i i ) (ii) (ii) 对所有 A ∈ F , ∫ A X d P = ∫ A Y d P A \in \mathcal{F}, \int_{A} X d P=\int_{A} Y d P A∈F,∫AXdP=∫AYdP.
任意满足 ( i ) (i) (i)和 ( i i ) (ii) (ii)的随机变量 Y Y Y被称为 E ( X ∣ F ) E(X \mid \mathcal{F}) E(X∣F)的一个版本.
命题4.1.1. 条件期望的等价定义 Y ∈ F Y \in \mathscr{F} Y∈F 等于 E [ X ∣ F ] E[X\mid \mathscr{F}] E[X∣F] 的充要条件是: 对任意有界的 Y ∈ F Y \in \mathscr{F} Y∈F 有
E [ X θ ] = E [ Y θ ] E[X\theta]=E[Y \theta] E[Xθ]=E[Yθ].
证明:充分性显然. 又若 η = E [ ξ ∣ G ] \eta=E[\xi \mid \mathscr{G}] η=E[ξ∣G], 则由定义当 θ = 1 A , A ∈ G \theta=1_{A}, A \in \mathscr{G} θ=1A,A∈G 时该式是成立的. 一般情况由单调类定理推出.
1.2. 条件期望的存在唯一性
引理 4.1.1.条件期望的可积性 . 上述满足 ( i ) (i) (i)和 ( i i ) (ii) (ii)的随机变量 Y Y Y可积.
对于 A = { Y > 0 } ∈ F A=\{Y > 0\}\in \mathcal{F} A={Y>0}∈F, 有
E ∣ Y ∣ = ∫ A Y d P − ∫ A c Y d P = ∫ A X d P − ∫ A c ( − X ) d P ≤ E ∣ X ∣ E|Y|=\int_A Y dP-\int_{A^c} Y dP=\int_A XdP-\int_{A^c}(-X)dP\leq E|X| E∣Y∣=∫AYdP−∫AcYdP=∫AXdP−∫Ac(−X)dP≤E∣X∣
下面的定理4.4.1和定理4.4.1*证明了条件期望的存在性和唯一性,
定理 4.4.1 条件期望的唯一性(a.s.) 如果随机变量 Y , Y ′ Y,Y' Y,Y′满足 ( i ) (i) (i)和 ( i i ) (ii) (ii), 则 Y = Y ′ , a . s . Y=Y', a.s. Y=Y′,a.s..
证明:取 Y ′ Y' Y′满足条件 ( i ) ( i i ) (i)(ii) (i)(ii), 令 A = { Y − Y ′ ≥ ϵ > 0 } A=\left\{Y-Y^{\prime} \geq \epsilon>0\right\} A={Y−Y′≥ϵ>0},
0 = ∫ A X − X d P = ∫ A Y − Y ′ d P ≥ ϵ P ( A ) 0=\int_{A} X-X d P=\int_{A} Y-Y^{\prime} d P \geq \epsilon P(A) 0=∫AX−XdP=∫AY−Y′dP≥ϵP(A)
可得 P ( A ) = 0 P(A)=0 P(A)=0, 交换 Y Y Y和 Y ′ Y' Y′, 则 Y = Y ′ , a . s . Y=Y', a.s. Y=Y′,a.s.. 因此 Y = E ( X ∣ F ) Y=E(X|\mathcal{F}) Y=E(X∣F)是a.s.意义下的.
定理4.1.2 . 对于 B ∈ F B\in\mathcal{F} B∈F, 在 B B B上, 若 X 1 = X 2 X_{1}=X_{2} X1=X2,则 E ( X 1 ∣ F ) = E ( X 2 ∣ F ) E\left(X_{1} \mid \mathcal{F}\right)=E\left(X_{2} \mid \mathcal{F}\right) E(X1∣F)=E(X2∣F) a.s.
通过定理4.4.1相同的方法可证, 这个定理直接说明条件期望的唯一性.
定理 4.4.1. 条件期望存在性(猜测+验证) 对于 ∀ A ∈ F \forall A \in \mathcal{F} ∀A∈F, 令 μ ( A ) : = P ( A ) \mu(A):=P(A) μ(A):=P(A), ν ( A ) : = ∫ A X d P \nu(A):=\int_{A} X d P ν(A):=∫AXdP, 则 ν ≪ μ \nu \ll \mu ν≪μ, 且 d v / d μ dv/d\mu dv/dμ是条件期望.
证明:
- (1) 猜测 d v / d μ dv/d\mu dv/dμ是条件期望的一个版本, 对于 X ≥ 0 X\geq 0 X≥0, 利用习题1.5.4可以证明 ν \nu ν是测度,利用Radon-Nikodym 定理可以验证其满足条件 ( i ) ( i i ) (i)(ii) (i)(ii).
- (2) 对于一般的 X X X, 利用 X = X + − X − X=X^{+}-X^{-} X=X+−X−即可.
这个定理的证明说明限制在子集 A = { ω : Y ( ω ) ∈ B } A=\{\omega: Y(\omega)\in B\} A={ω:Y(ω)∈B}上, 把子集的概率归一化后求得的期望值是条件期望的一个版本. 下面的例子都是以这种形式给出(即本科学到的条件期望的定义).
2. 条件期望的示例
可以认为 F \mathcal{F} F描述了我们所掌握的信息,即对于每一个 A ∈ F A\in \mathcal{F} A∈F,我们知道事件 A A A是否发生了, E ( X ∣ F ) E(X|F) E(X∣F)是在所获得信息下对 X X X值的“最佳猜测”. 这个是条件期望的几何性质, 也是给出条件期望如此定义的原因(个人感觉从这个角度来看比较好理解).
下面示例的证明方法都是“猜测和验证”, 即猜测条件期望具体的表示公式, 然后检查它是否满足条件期望的定义 ( i ) (i) (i)和 ( i i ) (ii) (ii). 可以看到后面几个例子都是按照定理4.4.1*这个条件期望的版本给出的. 即限制在子集 A = { ω : Y ( ω ) ∈ B } A=\{\omega: Y(\omega)\in B\} A={ω:Y(ω)∈B}上, 把子集的概率归一化后求得的期望值是条件期望的一个版本.
2.1. X ∈ F X \in \mathcal{F} X∈F, X X X与 F \mathcal{F} F独立的情形
示例 4.1.3. X ∈ F X \in \mathcal{F} X∈F的情形 如果 X ∈ F X \in \mathcal{F} X∈F, 则 E ( X ∣ F ) = X E(X \mid \mathcal{F})=X E(X∣F)=X; i.e., 即已知 X X X,则“最佳猜测”是 X X X本身. 特例是 X = c X=c X=c, c c c是常数.
示例 4.1.4. X X X与 F \mathcal{F} F独立的情形 假设 X X X与 F \mathcal{F} F独立, 即对于所有 B ∈ R B \in \mathcal{R} B∈R, A ∈ F A \in \mathcal{F} A∈F,有
P ( { X ∈ B } ∩ A ) = P ( X ∈ B ) P ( A ) P(\{X \in B\} \cap A)=P(X \in B) P(A) P({X∈B}∩A)=P(X∈B)P(A)这种情形下, E ( X ∣ F ) = E X E(X \mid \mathcal{F})=E X E(X∣F)=EX; 即如果对 X X X一无所知, 则“最佳猜测”是 E X E X EX.
2.2. X X X是有限 σ \sigma σ代数情形
我们将条件期望的新定义与本科概率课程中教授的第一个定义联系起来.
示例 4.1.5.有限 σ \sigma σ代数时的条件期望 假设 Ω 1 , Ω 2 , . . . \Omega_1,\Omega_2,... Ω1,Ω2,...是 Ω \Omega Ω有限划分为不相交的集,每个集都有正概率,设 F = σ ( Ω 1 , Ω 2 , . . . ) \mathcal{F}=\sigma(\Omega_1,\Omega_2,...) F=σ(Ω1,Ω2,...)是由这些集合生成的 σ \sigma σ域. F \mathcal{F} F的结构为
F = { ∅ , ∑ i = 1 m Ω n i : m = 0 , 1 , ⋯ , n ; 1 ≤ n 1 < n 2 < ⋯ n m ≤ n , } \mathscr{F}=\left\{\emptyset, \sum_{i=1}^{m} \Omega_{n_{i}}: m=0,1, \cdots, n ; 1 \leq n_{1}<n_{2}<\cdots n_{m} \leq n,\right\} F={∅,i=1∑mΩni:m=0,1,⋯,n;1≤n1<n2<⋯nm≤n,}
设 X ∈ L 1 ( F ) X \in L^{1}(\mathscr{F}) X∈L1(F), 则 E [ X ∣ F ] = ∑ i = 1 n α i 1 Ω i , 其中 , α i : = 1 P ( Ω i ) E [ X 1 Ω i ] E[X \mid \mathscr{F}]=\sum_{i=1}^{n} \alpha_{i} 1_{\Omega_{i}},\text{其中}, \alpha_{i}:=\frac{1}{P\left(\Omega_{i}\right)} E\left[X 1_{\Omega_{i}}\right] E[X∣F]=∑i=1nαi1Ωi,其中,αi:=P(Ωi)1E[X1Ωi].
注释:(i) 换句话说, Ω i \Omega_i Ωi中的信息告诉我们, 我们的结果位于分区的哪个元素中, 并且给定这个信息, 对X的最佳猜测是 X X X对 Ω i \Omega_i Ωi的平均值; (ii)一个退化但是重要的情形是 F = { ∅ , Ω } \mathcal{F}=\{\emptyset, \Omega\} F={∅,Ω}, 有 E ( X ∣ F ) = E X E(X \mid \mathcal{F})=E X E(X∣F)=EX.
这和本科学过的全概率公式联系起来了,令
P ( A ∣ G ) = E ( 1 A ∣ G ) , P ( A ∣ B ) = P ( A ∩ B ) / P ( B ) P(A \mid \mathcal{G})=E\left(1_{A} \mid \mathcal{G}\right), P(A \mid B) =P(A \cap B) / P(B) P(A∣G)=E(1A∣G),P(A∣B)=P(A∩B)/P(B)
在这个例子里面,在 Ω i \Omega_{i} Ωi上,有 P ( A ∣ F ) = P ( A ∣ Ω i ) P(A \mid \mathcal{F})=P\left(A \mid \Omega_{i}\right) P(A∣F)=P(A∣Ωi),即
习题 4.1.1. 全概率公式, Bayes公式
I. 利用示例4.1.5证明全概率公式
P ( A ) = ∑ i = 1 n P ( A ∣ Ω i ) P ( Ω i ) P(A)=\sum_{i=1}^{n} P\left(A \mid \Omega_{i}\right) P\left(\Omega_{i}\right) P(A)=i=1∑nP(A∣Ωi)P(Ωi)
II. 令 G ∈ G G \in \mathcal{G} G∈G, (i) 利用示例4.1.5证明
P ( G ∣ A ) = ∫ G P ( A ∣ G ) d P / ∫ Ω P ( A ∣ G ) d P P(G \mid A)=\int_{G} P(A \mid \mathcal{G}) d P / \int_{\Omega} P(A \mid \mathcal{G}) d P P(G∣A)=∫GP(A∣G)dP/∫ΩP(A∣G)dP
(ii) 当 G \mathcal{G} G是由集的划分生成的 σ \sigma σ-代数, 这将变成一般的贝叶斯公式
P ( G i ∣ A ) = P ( A ∣ G i ) P ( G i ) / ∑ j P ( A ∣ G j ) P ( G j ) P\left(G_{i} \mid A\right)=P\left(A \mid G_{i}\right) P\left(G_{i}\right) / \sum_{j} P\left(A \mid G_{j}\right) P\left(G_{j}\right) P(Gi∣A)=P(A∣Gi)P(Gi)/j∑P(A∣Gj)P(Gj)
证明:I. 在示例4.1.5的结论中对 E [ X ∣ F ] E[X \mid \mathscr{F}] E[X∣F] 取期望, 得到
E [ X ] = ∑ i = 1 n 1 P ( Ω i ) E [ X 1 Ω i ] P ( Ω i ) . E[X]=\sum_{i=1}^{n} \frac{1}{P\left(\Omega_{i}\right)} E\left[X 1_{\Omega_{i}}\right] P\left(\Omega_{i}\right) . E[X]=i=1∑nP(Ωi)1E[X1Ωi]P(Ωi).
特别当 X = 1 A , A ∈ F X=1_{A}, A \in \mathscr{F} X=1A,A∈F 时, 可得全概率公式.
II. (ii) 由(i) 结合全概率公式可得.(i) 根据条件期望的定义可得
P ( G ∣ A ) = P ( G ∩ A ) P ( A ) = ∫ G 1 A d P ∫ Ω 1 A d P = ∫ G P ( A ∣ G ) d P ∫ Ω P ( A ∣ G ) d P P(G \mid A)=\frac{P(G \cap A)}{P(A)}=\frac{\int_{G} 1_{A} d P}{\int_{\Omega} 1_{A} d P}=\frac{\int_{G} P(A \mid \mathcal{G}) d P}{\int_{\Omega} P(A \mid \mathcal{G}) d P} P(G∣A)=P(A)P(G∩A)=∫Ω1AdP∫G1AdP=∫ΩP(A∣G)dP∫GP(A∣G)dP
2.3. X X X是随机变量生成的 σ \sigma σ域
给定 σ \sigma σ域的条件期望的定义包含对随机变量的条件作为特殊情况 E ( X ∣ Y ) = E ( X ∣ σ ( Y ) ) E(X \mid Y)=E(X \mid \sigma(Y)) E(X∣Y)=E(X∣σ(Y)), 其中, σ ( Y ) \sigma(Y) σ(Y) 是由 Y Y Y生成的 σ \sigma σ-代数. 由于 E [ ξ ∣ G ] E[\xi \mid \mathscr{G}] E[ξ∣G] 关于 G \mathscr{G} G 可测, 因而存在Borel函数 φ \varphi φ 使得 φ ( η ) = E [ ξ ∣ η ] \varphi(\eta)=E[\xi \mid \eta] φ(η)=E[ξ∣η], 因此我们自然定义 E [ ξ ∣ η = x ] = φ ( x ) E[\xi \mid \eta=x]=\varphi(x) E[ξ∣η=x]=φ(x), φ \varphi φ 在通常的意义下自然不是唯一的. 例如, 在 Y Y Y 的值域之外, 它可以任意取值, 只要保证 φ \varphi φ 是Borel可测就行.
定理 4.1.6 给定随机变量条件期望的唯一版本 对任意 B ∈ B B \in \mathscr{B} B∈B, μ ( B ) : = P ( Y − 1 ( B ) ) , ν ( B ) : = ∫ Y − 1 ( B ) X d P \mu(B):=P\left(Y^{-1}(B)\right), \nu(B):=\int_{Y^{-1}(B)} X d P μ(B):=P(Y−1(B)),ν(B):=∫Y−1(B)XdP, 则
ν ≪ μ , φ = d ν / d μ , μ − a . e . \nu \ll \mu, \varphi={d \nu}/{d \mu}, \mu-a.e. ν≪μ,φ=dν/dμ,μ−a.e.
证明: ν ≪ μ \nu \ll \mu ν≪μ 是显然的. 又对于任意有界Borel 函数 ψ \psi ψ, 有
∫ R ψ ( x ) φ ( x ) d μ = E [ ψ ( η ) φ ( η ) ] = E [ ψ ( η ) E [ ξ ∣ η ] ] = E [ E [ ψ ( η ) ξ ∣ η ] ] = E [ ψ ( η ) ξ ] = ∫ R ψ ( x ) ν ( d x ) \begin{aligned} \int_{\mathbb{R}} \psi(x) \varphi(x) d \mu &=E[\psi(\eta) \varphi(\eta)] =E[\psi(\eta) E[\xi \mid \eta]] \\ &=E[E[\psi(\eta) \xi \mid \eta]] =E[\psi(\eta) \xi]=\int_{\mathbb{R}} \psi(x) \nu(d x) \end{aligned} ∫Rψ(x)φ(x)dμ=E[ψ(η)φ(η)]=E[ψ(η)E[ξ∣η]]=E[E[ψ(η)ξ∣η]]=E[ψ(η)ξ]=∫Rψ(x)ν(dx)
这就证明了结论. 在上面所铺开的式子中, 最后一步成立的理由如下: 设 ψ \psi ψ 是简单函数 ψ ( x ) = ∑ i = 1 n a i 1 B i ( x ) \psi(x)=\sum_{i=1}^{n} a_{i} 1_{B_{i}}(x) ψ(x)=∑i=1nai1Bi(x), 则
E [ ψ ( η ) ξ ] = ∑ i = 1 n a i E [ 1 B i ( η ) ξ ] = ∑ i = 1 n a i ∫ η − 1 ( B i ) ξ d P = ∑ i = 1 n a i ν ( B i ) = ∫ ψ d ν . E[\psi(\eta) \xi] =\sum_{i=1}^{n} a_{i} E\left[1_{B_{i}}(\eta) \xi\right]=\sum_{i=1}^{n} a_{i} \int_{\eta^{-1}\left(B_{i}\right)} \xi d P =\sum_{i=1}^{n} a_{i} \nu\left(B_{i}\right)=\int \psi d \nu . E[ψ(η)ξ]=i=1∑naiE[1Bi(η)ξ]=i=1∑nai∫η−1(Bi)ξdP=i=1∑naiν(Bi)=∫ψdν.
一般情况可通过简单函数逼近得到.
示例 4.1.6 (某随机变量函数关于另一个随机变量的条件期望)] 假设 X X X 和 Y Y Y联合密度 f ( x , y ) f(x, y) f(x,y), 即
P ( ( X , Y ) ∈ B ) = ∫ B f ( x , y ) d x d y for B ∈ R 2 P((X, Y) \in B)=\int_{B} f(x, y) d x d y \quad \text { for } B \in \mathcal{R}^{2} P((X,Y)∈B)=∫Bf(x,y)dxdy for B∈R2
假设对所有 y y y,有 ∫ f ( x , y ) d x > 0 \int f(x, y) d x>0 ∫f(x,y)dx>0. 则如果 E ∣ g ( X ) ∣ < ∞ E|g(X)|<\infty E∣g(X)∣<∞,有
E ( g ( X ) ∣ Y ) = ∫ g ( x ) f ( x , Y ) d x / ∫ f ( x , Y ) d x E(g(X) \mid Y)=\int g(x) f(x, Y) d x / \int f(x, Y) d x E(g(X)∣Y)=∫g(x)f(x,Y)dx/∫f(x,Y)dx
证明:由示例4.1.5,我们可以知道
P ( X = x ∣ Y = y ) = P ( X = x , Y = y ) P ( Y = y ) = f ( x , y ) ∫ f ( x , y ) d x P(X=x \mid Y=y)=\frac{P(X=x, Y=y)}{P(Y=y)}=\frac{f(x, y)}{\int f(x, y) d x} P(X=x∣Y=y)=P(Y=y)P(X=x,Y=y)=∫f(x,y)dxf(x,y)
那么可以猜测该定理的结论成立,下面去验证对 A = { ω : Y ( ω ) ∈ B } A=\{\omega: Y(\omega) \in B\} A={ω:Y(ω)∈B}, B ∈ R B \in \mathcal{R} B∈R,有
E ( h ( Y ) ; A ) = ∫ B ∫ h ( y ) f ( x , y ) d x d y = ∫ B ∫ g ( x ) f ( x , y ) d x d y = E ( g ( X ) 1 B ( Y ) ) = E ( g ( X ) ; A ) \begin{aligned} E(h(Y) ; A) &=\int_{B} \int h(y) f(x, y) d x d y=\int_{B} \int g(x) f(x, y) d x d y \\ &=E\left(g(X) 1_{B}(Y)\right)=E(g(X) ; A) \end{aligned} E(h(Y);A)=∫B∫h(y)f(x,y)dxdy=∫B∫g(x)f(x,y)dxdy=E(g(X)1B(Y))=E(g(X);A)
示例 4.1.7 (二元独立随机变量函数关于某变量的条件期望) 假设 X X X, Y Y Y独立. 令 φ \varphi φ是满足 E ∣ φ ( X , Y ) ∣ < ∞ E|\varphi(X, Y)|<\infty E∣φ(X,Y)∣<∞的函数,有
E ( φ ( X , Y ) ∣ X ) = g ( X ) E(\varphi(X, Y) \mid X)=g(X) E(φ(X,Y)∣X)=g(X)
其中, g ( x ) = E ( φ ( x , Y ) ) g(x)=E(\varphi(x, Y)) g(x)=E(φ(x,Y)).
证明:显然 g ( X ) ∈ σ ( X ) g(X) \in \sigma(X) g(X)∈σ(X). 验证 (ii), 如果 A ∈ σ ( X ) A \in \sigma(X) A∈σ(X), 则 A = { X ∈ C } A=\{X \in C\} A={X∈C}, 由变量代换
以及 ( X , Y ) (X, Y) (X,Y)是乘积测度 (定理 2.1.11), 则 g g g的定义和再次的变量代换
∫ A φ ( X , Y ) d P = E { φ ( X , Y ) 1 C ( X ) } = ∬ ϕ ( x , y ) 1 C ( x ) ν ( d y ) μ ( d x ) = ∫ 1 C ( x ) g ( x ) μ ( d x ) = ∫ A g ( X ) d P \begin{aligned} \int_{A} \varphi(X, Y) d P &=E\left\{\varphi(X, Y) 1_{C}(X)\right\} =\iint \phi(x, y) 1_{C}(x) \nu(d y) \mu(d x) \\ &=\int 1_{C}(x) g(x) \mu(d x)=\int_{A} g(X) d P \end{aligned} ∫Aφ(X,Y)dP=E{φ(X,Y)1C(X)}=∬ϕ(x,y)1C(x)ν(dy)μ(dx)=∫1C(x)g(x)μ(dx)=∫Ag(X)dP
对示例4.1.7求期望 设 X ∈ L 1 ( F ) , Y X \in L^{1}(\mathscr{F}), Y X∈L1(F),Y 的分布函数为 F , h F, h F,h 为有界 Borel函数. 则
E [ h ( Y ) X ] = ∫ − ∞ ∞ h ( y ) E [ X ∣ Y = y ] d F ( y ) E[h(Y) X]=\int_{-\infty}^{\infty} h(y) E[X \mid Y=y] d F(y) E[h(Y)X]=∫−∞∞h(y)E[X∣Y=y]dF(y)
证明: Method 1 . 在示例4.1.7中,令 φ ( x , y ) = h ( y ) x \varphi(x, y)=h(y)x φ(x,y)=h(y)x, 则
E ( h ( Y ) X ∣ Y ) = g ( Y ) E(h(Y)X \mid Y)=g(Y) E(h(Y)X∣Y)=g(Y)
其中, g ( y ) = E ( h ( y ) X ) g(y)=E(h(y)X) g(y)=E(h(y)X). 对上式求期望可证.
Method 2 记 φ ( η ) : = E [ ξ ∣ η ] \varphi(\eta):=E[\xi \mid \eta] φ(η):=E[ξ∣η]. 有
E [ h ( η ) ξ ] = E [ E [ h ( η ) ξ ∣ η ] ] = E [ h ( η ) φ ( η ) ] = ∫ − ∞ ∞ h ( x ) φ ( x ) d F ( x ) = ∫ − ∞ ∞ h ( x ) E [ ξ ∣ η = x ] d F ( x ) \begin{aligned} E[h(\eta) \xi] &=E[E[h(\eta) \xi \mid \eta]] =E[h(\eta) \varphi(\eta)] \\ &=\int_{-\infty}^{\infty} h(x) \varphi(x) d F(x) =\int_{-\infty}^{\infty} h(x) E[\xi \mid \eta=x] d F(x) \end{aligned} E[h(η)ξ]=E[E[h(η)ξ∣η]]=E[h(η)φ(η)]=∫−∞∞h(x)φ(x)dF(x)=∫−∞∞h(x)E[ξ∣η=x]dF(x)
2.4. Borel悖论
示例 4.1.8.Borel paradox 若 X X X在地球上均匀分布,那么看起来 θ \theta θ和大圆上的角度 ϕ \phi ϕ在它们的可能取值上都应该是均匀分布. 实际上 θ \theta θ均匀分布, 但 ϕ \phi ϕ不是.
设 X X X是地球上随机选择的一个点,设 θ \theta θ是它的经度, ϕ \phi ϕ是它的纬度.通常我们可以选择 θ ∈ [ 0 , 2 π ) \theta\in [0,2\pi) θ∈[0,2π)和 ϕ ∈ ( − π / 2 , π / 2 ] \phi \in (- \pi/2,\pi/2] ϕ∈(−π/2,π/2], 但我们同样可以选择 θ ∈ [ 0 , π ) \theta\in[0,\pi) θ∈[0,π)和 ϕ ∈ ( − π , π ] \phi\in (−\pi,\pi] ϕ∈(−π,π].新的经度指定了该点所在的大圆, ϕ \phi ϕ给出了该角度.
证明:如果意识到在新的或传统的公式中 θ \theta θ独立于 ϕ \phi ϕ, 即条件分布是无条件分布, 这就不再是悖论. 考虑到赤道附近的陆地比北极附近多,所以不均匀.
3. 条件期望的性质
3.1. 常规性质
定理 4.1.9 (条件期望的常规性质:线性和单调) 假设 E ∣ X ∣ , E ∣ Y ∣ < ∞ E|X|, E|Y|<\infty E∣X∣,E∣Y∣<∞. 条件期望是线性单调的.
定理 4.1.9 (条件期望的收敛定理) 设 ξ 0 \xi_{0} ξ0可积随机变量, { ξ n , n ≥ 1 } \left\{\xi_{n}, n \geq 1\right\} {ξn,n≥1}为随机变量列
- (单调收敛定理)若 ξ 0 ≤ ξ n ↑ ξ \xi_{0} \leq \xi_{n} \uparrow \xi ξ0≤ξn↑ξ, 或 ξ 0 ≥ ξ n ↓ ξ \xi_{0} \geq \xi_{n} \downarrow \xi ξ0≥ξn↓ξ, 则 lim n → ∞ E [ ξ n ∣ G ] = E [ ξ ∣ G ] \lim _{n \rightarrow \infty} E\left[\xi_{n} \mid \mathscr{G}\right]=E[\xi \mid \mathscr{G}] limn→∞E[ξn∣G]=E[ξ∣G];
- (Fatou引理)若 ξ n ≥ ξ 0 \xi_{n} \geq \xi_{0} ξn≥ξ0, 则 E [ lim inf n → ∞ ξ n ∣ G ] ≤ lim inf n → ∞ E [ ξ n ∣ G ] E\left[\liminf _{n \rightarrow \infty} \xi_{n} \mid \mathscr{G}\right] \leq \liminf _{n \rightarrow \infty} E\left[\xi_{n} \mid \mathscr{G}\right] E[liminfn→∞ξn∣G]≤liminfn→∞E[ξn∣G]. 若 ξ n ≤ ξ 0 \xi_{n} \leq \xi_{0} ξn≤ξ0, 则 E [ lim sup n → ∞ ξ n ∣ G ] ≥ lim sup n → ∞ E [ ξ n ∣ G ] E\left[\limsup _{n \rightarrow \infty} \xi_{n} \mid \mathscr{G}\right] \geq \limsup _{n \rightarrow \infty} E\left[\xi_{n} \mid \mathscr{G}\right] E[limsupn→∞ξn∣G]≥limsupn→∞E[ξn∣G];
- (控制收敛定理)若 ∣ ξ n ∣ ≤ ξ , ξ n → ξ \left|\xi_{n}\right| \leq \xi, \xi_{n} \rightarrow \xi ∣ξn∣≤ξ,ξn→ξ a.s., 则 E [ lim n → ∞ ξ n ∣ G ] = lim n → ∞ E [ ξ n ∣ G ] E\left[\lim _{n \rightarrow \infty} \xi_{n} \mid \mathscr{G}\right]=\lim _{n \rightarrow \infty} E\left[\xi_{n} \mid \mathscr{G}\right] E[limn→∞ξn∣G]=limn→∞E[ξn∣G]
证明的思路是 单调收敛定理 ⇒ \Rightarrow ⇒Fatou引理 ⇒ \Rightarrow ⇒控制收敛定理. 由一致可积性所保证的收敛定理不再成立.
-
(i) 设 θ = l i m n E [ ξ n ∣ G ] \theta=lim_nE\left[\xi_{n} \mid \mathscr{G}\right] θ=limnE[ξn∣G], 则 θ ∈ G \theta \in \mathscr{G} θ∈G. (ii) 因为 ξ n \xi_{n} ξn 单升, 所以 E [ ξ n ∣ G ] E\left[\xi_{n} \mid \mathscr{G}\right] E[ξn∣G] 单升. 又 E [ ξ n ∣ G ] ≥ E\left[\xi_{n} \mid \mathscr{G}\right] \geq E[ξn∣G]≥ E [ ξ 0 ∣ G ] E\left[\xi_{0} \mid \mathscr{G}\right] E[ξ0∣G], 所以由单调收敛定理, 对任意 A ∈ G A \in \mathscr{G} A∈G 有
∫ A θ d P = lim n → ∞ ∫ A E [ ξ n ∣ G ] d P = lim n → ∞ ∫ A ξ n d P = ∫ A ξ d P \int_{A} \theta d P =\lim _{n \rightarrow \infty} \int_{A} E\left[\xi_{n} \mid \mathscr{G}\right] d P=\lim _{n \rightarrow \infty} \int_{A} \xi_{n} d P=\int_{A} \xi d P ∫AθdP=n→∞lim∫AE[ξn∣G]dP=n→∞lim∫AξndP=∫AξdP
所以 l i m n E [ ξ n ∣ G ] = E [ ξ ∣ G ] lim_nE\left[\xi_{n} \mid \mathscr{G}\right]=E[\xi \mid \mathscr{G}] limnE[ξn∣G]=E[ξ∣G]. -
记 η n = inf k ≥ n ξ k \eta_{n}=\inf _{k \geq n} \xi_{k} ηn=infk≥nξk. 则 ξ 0 ≤ η n ↑ lim inf n → ∞ ξ n , E [ η n ∣ G ] ≤ E [ ξ n ∣ G ] \xi_{0} \leq \eta_{n} \uparrow \liminf _{n \rightarrow \infty} \xi_{n}, E\left[\eta_{n} \mid \mathscr{G}\right] \leq E\left[\xi_{n} \mid \mathscr{G}\right] ξ0≤ηn↑n→∞liminfξn,E[ηn∣G]≤E[ξn∣G]
因此由单调收敛定理可得,
E [ lim inf n → ∞ ξ n ∣ G ] = lim n → ∞ E [ η n ∣ G ] ≤ lim inf n → ∞ E [ ξ n ∣ G ] E\left[\liminf _{n \rightarrow \infty} \xi_{n} \mid \mathscr{G}\right] =\lim _{n \rightarrow \infty} E\left[\eta_{n} \mid \mathscr{G}\right] \leq \liminf _{n \rightarrow \infty} E\left[\xi_{n} \mid \mathscr{G}\right] E[n→∞liminfξn∣G]=n→∞limE[ηn∣G]≤n→∞liminfE[ξn∣G] -
用刚刚证明的Fatou引理有
E [ ξ ∣ G ] = E [ lim n ξ n ∣ G ] ≤ lim inf n → ∞ E [ ξ n ∣ G ] ≤ lim sup n → ∞ E [ ξ n ∣ G ] ≤ E [ lim n ξ n ∣ G ] = E [ ξ ∣ G ] . \begin{aligned} E[\xi \mid \mathscr{G}] &=E\left[\lim _{n} \xi_{n} \mid \mathscr{G}\right] \leq \liminf _{n \rightarrow \infty} E\left[\xi_{n} \mid \mathscr{G}\right] \\ & \leq \limsup _{n \rightarrow \infty} E\left[\xi_{n} \mid \mathscr{G}\right] \leq E\left[\lim _{n} \xi_{n} \mid \mathscr{G}\right]=E[\xi \mid \mathscr{G}] . \end{aligned} E[ξ∣G]=E[nlimξn∣G]≤n→∞liminfE[ξn∣G]≤n→∞limsupE[ξn∣G]≤E[nlimξn∣G]=E[ξ∣G].
3.2. 条件不等式
定理4.1.11.条件Jensen不等式 如果 φ \varphi φ是凸函数, E ∣ X ∣ , E ∣ φ ( X ) ∣ < ∞ E|X|, E|\varphi(X)|<\infty E∣X∣,E∣φ(X)∣<∞,则 φ ( E ( X ∣ F ) ) ≤ E ( φ ( X ) ∣ F ) \varphi(E(X \mid \mathcal{F})) \leq E(\varphi(X) \mid \mathcal{F}) φ(E(X∣F))≤E(φ(X)∣F).
证明: Method 1 . 令 S = { ( a , b ) : a , b ∈ Q , a x + b ≤ φ ( x ) S=\{(a, b): a, b \in \mathbf{Q}, a x+b \leq \varphi(x) S={(a,b):a,b∈Q,ax+b≤φ(x) for all x } x\} x},则 φ ( x ) = sup { a x + b : ( a , b ) ∈ S } \varphi(x)=\sup \{a x+b:(a, b) \in S\} φ(x)=sup{ax+b:(a,b)∈S}. 若 φ ( x ) ≥ a x + b \varphi(x) \geq a x+b φ(x)≥ax+b,由条件期望的线性性和单调性,可得
E ( φ ( X ) ∣ F ) ≥ a E ( X ∣ F ) + b , a.s. E(\varphi(X) \mid \mathcal{F}) \geq a E(X \mid \mathcal{F})+b, \text { a.s. } E(φ(X)∣F)≥aE(X∣F)+b, a.s.
在 ( a , b ) ∈ S (a, b) \in S (a,b)∈S上取上界,可得 E ( φ ( X ) ∣ F ) ≥ φ ( E ( X ∣ F ) ) , a.s. E(\varphi(X) \mid \mathcal{F}) \geq \varphi(E(X \mid \mathcal{F})), \text { a.s. } E(φ(X)∣F)≥φ(E(X∣F)), a.s. .
Method 2 . 和积分时一样, 我们同样利用凸函数的性质:
φ ( x ) − φ ( y ) ≥ φ + ′ ( y ) ( x − y ) . \varphi(x)-\varphi(y) \geq \varphi_{+}^{\prime}(y)(x-y) . φ(x)−φ(y)≥φ+′(y)(x−y).
因此 φ ( ξ ) − φ ( E [ ξ ∣ G ] ) ≥ φ + ′ ( E [ ξ ∣ G ] ) ( ξ − E [ ξ ∣ G ] ) \varphi(\xi)-\varphi(E[\xi \mid \mathscr{G}]) \geq \varphi_{+}^{\prime}(E[\xi \mid \mathscr{G}])(\xi-E[\xi \mid \mathscr{G}]) φ(ξ)−φ(E[ξ∣G])≥φ+′(E[ξ∣G])(ξ−E[ξ∣G]).
相比期望, 现在出现的新情况是右端未必可积, 故上式不能直接用来取条件期望(引理4.1.1).
令 A n : = { ∣ E [ ξ ∣ G ] ∣ ≤ n } A_{n}:= \{|E[\xi \mid \mathscr{G}]| \leq n\} An:={∣E[ξ∣G]∣≤n},
ξ n : = ξ 1 A n \xi_{n}:=\xi 1_{A_{n}} ξn:=ξ1An, 上式以 ξ n \xi_{n} ξn 代 ξ \xi ξ 并求关于 G \mathscr{G} G的条件期望
E [ φ ( ξ n ) ∣ G ] ≥ φ ( E [ ξ n ∣ G ] ) E\left[\varphi\left(\xi_{n}\right) \mid \mathscr{G}\right] \geq \varphi\left(E\left[\xi_{n} \mid \mathscr{G}\right]\right) E[φ(ξn)∣G]≥φ(E[ξn∣G])
对于右式, E [ ξ n ∣ G ] = 1 A n E [ ξ ∣ G ] E\left[\xi_{n} \mid \mathscr{G}\right]=1_{A_{n}} E[\xi \mid \mathscr{G}] E[ξn∣G]=1AnE[ξ∣G]; 对于左式,
E [ φ ( ξ n ) ∣ G ] = E [ φ ( ξ ) 1 A n + φ ( 0 ) 1 A n c ∣ G ] = E [ φ ( ξ ) ∣ G ] 1 A n + φ ( 0 ) 1 A n c , \begin{gathered} E\left[\varphi\left(\xi_{n}\right) \mid \mathscr{G}\right]=E\left[\varphi(\xi) 1_{A_{n}}+\varphi(0) 1_{A_{n}^{c}} \mid \mathscr{G}\right]\\ =E[\varphi(\xi) \mid \mathscr{G}] 1_{A_{n}}+\varphi(0) 1_{A_{n}^{c}}, \end{gathered} E[φ(ξn)∣G]=E[φ(ξ)1An+φ(0)1Anc∣G]=E[φ(ξ)∣G]1An+φ(0)1Anc,
取 n → ∞ n \rightarrow \infty n→∞, 用条件期望的控制收敛定理可得.
推论 4.1.11.条件期望是 L p L^{p} Lp中的收缩算子 条件期望是 L p L^{p} Lp中的收缩算子, 即 E ( ∣ E ( X ∣ F ) ∣ p ) ≤ E ∣ X ∣ p E\left(|E(X \mid \mathcal{F})|^{p}\right) \leq E|X|^{p} E(∣E(X∣F)∣p)≤E∣X∣p.
证明:取 φ = ∣ x ∣ p \varphi=|x|^p φ=∣x∣p,利用定理4.1.10可得 ∣ E ( X ∣ F ) ∣ p ≤ E ( ∣ X ∣ p ∣ F ) |E(X \mid \mathcal{F})|^{p} \leq E\left(|X|^{p} \mid \mathcal{F}\right) ∣E(X∣F)∣p≤E(∣X∣p∣F), 取期望
E ( ∣ E ( X ∣ F ) ∣ p ) ≤ E ( E ( ∣ X ∣ p ∣ F ) ) = E ∣ X ∣ p E\left(|E(X \mid \mathcal{F})|^{p}\right) \leq E\left(E\left(|X|^{p} \mid \mathcal{F}\right)\right)=E|X|^{p} E(∣E(X∣F)∣p)≤E(E(∣X∣p∣F))=E∣X∣p
习题4.1.4.条件Holder不等式, Minkowski不等式 1. 若 ξ ∈ L p , η ∈ L q , 1 < p , q < ∞ , p − 1 + q − 1 = 1 \xi \in L^{p}, \eta \in L^{q}, 1<p, q<\infty, p^{-1}+q^{-1}=1 ξ∈Lp,η∈Lq,1<p,q<∞,p−1+q−1=1, 则
E [ ∣ ξ η ∥ G ] ≤ ( E [ ∣ ξ ∣ p ∣ G ] ) 1 / p ( E [ ∣ η ∣ q ∣ G ] ) 1 / q E[\mid \xi \eta \| \mathscr{G}] \leq\left(E\left[|\xi|^{p} \mid \mathscr{G}\right]\right)^{1 / p}\left(E\left[|\eta|^{q} \mid \mathscr{G}\right]\right)^{1 / q} E[∣ξη∥G]≤(E[∣ξ∣p∣G])1/p(E[∣η∣q∣G])1/q
2. 若 ξ , η ∈ L p \xi, \eta \in L^{p} ξ,η∈Lp, 则 ( E [ ∣ ξ + η ∣ p ∣ G ] ) 1 / p ≤ ( E [ ∣ ξ ∣ p ∣ G ] ) 1 / p + ( E [ ∣ η ∣ p ∣ G ] ) 1 / p \left(E\left[|\xi+\eta|^{p} \mid \mathscr{G}\right]\right)^{1 / p} \leq\left(E\left[|\xi|^{p} \mid \mathscr{G}\right]\right)^{1 / p}+\left(E\left[|\eta|^{p} \mid \mathscr{G}\right]\right)^{1 / p} (E[∣ξ+η∣p∣G])1/p≤(E[∣ξ∣p∣G])1/p+(E[∣η∣p∣G])1/p
证明:利用定理4.1.16正则条件概率直接从Holder不等式得到条件Holder不等式.
习题 4.1.3.条件Cauchy-Schwarz不等式 证明条件Cauchy-Schwarz不等式, 即
E ( X Y ∣ G ) 2 ≤ E ( X 2 ∣ G ) E ( Y 2 ∣ G ) E(X Y \mid \mathcal{G})^{2} \leq E\left(X^{2} \mid \mathcal{G}\right) E\left(Y^{2} \mid \mathcal{G}\right) E(XY∣G)2≤E(X2∣G)E(Y2∣G)
证明:利用条件期望的线性性和单调性可得下式, 再利用 b 2 − 4 a c ≤ 0 b^{2}-4 a c \leq 0 b2−4ac≤0可证.
0 ≤ E ( ( X + θ Y ) 2 ∣ G ) = E ( X 2 ∣ G ) θ 2 + 2 E ( X Y ∣ G ) θ + E ( Y 2 ∣ G ) 0 \leq E\left((X+\theta Y)^{2} \mid \mathcal{G}\right)=E\left(X^{2} \mid \mathcal{G}\right) \theta^{2}+2 E(X Y \mid \mathcal{G}) \theta+E\left(Y^{2} \mid \mathcal{G}\right) 0≤E((X+θY)2∣G)=E(X2∣G)θ2+2E(XY∣G)θ+E(Y2∣G)
习题 4.1.2.条件Chebyshev不等式 如果 a > 0 a>0 a>0,则 P ( ∣ X ∣ ≥ a ∣ F ) ≤ a − 2 E ( X 2 ∣ F ) P(|X| \geq a \mid \mathcal{F}) \leq a^{-2} E\left(X^{2} \mid \mathcal{F}\right) P(∣X∣≥a∣F)≤a−2E(X2∣F).
证明: a 2 1 ( ∣ X ∣ > a ) ≤ X 2 a^{2} 1_{(|X|>a)} \leq X^{2} a21(∣X∣>a)≤X2, 由条件期望的单调性和线性性可证.
3.3. 特殊性质
引理4.1.12. 不同 σ \sigma σ代数条件期望相同的条件 如果 F ⊂ G \mathcal{F} \subset \mathcal{G} F⊂G, E ( X ∣ G ) ∈ F E(X \mid \mathcal{G}) \in \mathcal{F} E(X∣G)∈F, 则 E ( X ∣ F ) = E ( X ∣ G ) E(X \mid \mathcal{F})=E(X \mid \mathcal{G}) E(X∣F)=E(X∣G).
下面的引理直观的说明了如果多出的信息对随机变量的估计是无效的, 那么 F \mathcal{F} F下和更多信息 G \mathcal{G} G下对随机变量的估计是一样的.
证明:(i) E ( X ∣ G ) ∈ F E(X \mid \mathcal{G}) \in \mathcal{F} E(X∣G)∈F, 满足 X X X条件期望的第一个条件; (ii) F ⊂ G \mathcal{F} \subset \mathcal{G} F⊂G可证第二个.
定理 4.1.13. 多重条件期望-较小的 σ \sigma σ-代数总是获胜 如果 F 1 ⊂ F 2 \mathcal{F}_{1} \subset \mathcal{F}_{2} F1⊂F2,则 (i) E ( E ( X ∣ F 1 ) ∣ F 2 ) = E ( X ∣ F 1 ) E\left(E\left(X \mid \mathcal{F}_{1}\right) \mid \mathcal{F}_{2}\right)=E\left(X \mid \mathcal{F}_{1}\right) E(E(X∣F1)∣F2)=E(X∣F1)\
(ii) E ( E ( X ∣ F 2 ) ∣ F 1 ) = E ( X ∣ F 1 ) E\left(E\left(X \mid \mathcal{F}_{2}\right) \mid \mathcal{F}_{1}\right)=E\left(X \mid \mathcal{F}_{1}\right) E(E(X∣F2)∣F1)=E(X∣F1); 换句话说, .
证明: ( i ) (i) (i) 由于 E ( X ∣ F 1 ) ∈ F 2 E\left(X \mid \mathcal{F}_{1}\right) \in \mathcal{F}_{2} E(X∣F1)∈F2, 易证; ( i i ) (ii) (ii) 利用定理4.1.12可得.
习题 4.1.5. 不同顺序的多重条件期望可能不同 举例说明在 Ω = { a , b , c } \Omega=\{a, b, c\} Ω={a,b,c}上,有可能
E ( E ( X ∣ F 1 ) ∣ F 2 ) ≠ E ( E ( X ∣ F 2 ) ∣ F 1 ) E\left(E\left(X \mid \mathcal{F}_{1}\right) \mid \mathcal{F}_{2}\right) \neq E\left(E\left(X \mid \mathcal{F}_{2}\right) \mid \mathcal{F}_{1}\right) E(E(X∣F1)∣F2)=E(E(X∣F2)∣F1).
证明:令 F 1 = σ ( { a } ) \mathcal{F}_{1}=\sigma(\{a\}) F1=σ({a}), F 2 = σ ( { c } ) \mathcal{F}_{2}=\sigma(\{c\}) F2=σ({c}). 取 X ( b ) = 1 , X ( a ) = X ( c ) = 0 X(b)=1, X(a)=X(c)=0 X(b)=1,X(a)=X(c)=0.
定理 4.1.14. 外置: 关于 F \mathcal{F} F的条件期望, X ∈ F X\in \mathcal{F} X∈F会像常数一样被带到“积分”外]
如果 X ∈ F X \in \mathcal{F} X∈F, E ∣ Y ∣ , E ∣ X Y ∣ < ∞ E|Y|, E|X Y|<\infty E∣Y∣,E∣XY∣<∞,则 E ( X Y ∣ F ) = X E ( Y ∣ F ) E(X Y \mid \mathcal{F})=X E(Y \mid \mathcal{F}) E(XY∣F)=XE(Y∣F).
证明:分步依次证明示性函数,简单函数,非负函数,一般函数.
3.4. 几何性质
定理 4.1.15. 条件期望是与 X X X平均二次误差最小的随机变量 若 E X 2 < ∞ E X^{2}<\infty EX2<∞, E ( X ∣ F ) E(X \mid \mathcal{F}) E(X∣F)是最小化"平均二次误差" E ( X − Y ) 2 E(X-Y)^{2} E(X−Y)2的随机变量 Y ∈ F Y \in \mathcal{F} Y∈F.
记 T ξ = E [ ξ ∣ G ] T \xi=E[\xi \mid \mathscr{G}] Tξ=E[ξ∣G], 则 T T T为 L p ( F ) L^{p}(\mathscr{F}) Lp(F)上的幂等算子(即 T 2 = T T^{2}=T T2=T), 其值域为 L p ( G ) L^{p}(\mathscr{G}) Lp(G).
(i) 若 p = 2 p=2 p=2, 则条件期望是从 L 2 ( F ) L^{2}(\mathscr{F}) L2(F)到 L 2 ( G ) L^{2}(\mathscr{G}) L2(G)的投影算子, 即 G \mathscr{G} G中最接近 X X X的点.
(ii) 习题4.1.6的 几何含义是子空间 G \mathscr{G} G越大, 投影越接近, 或者统计含义是信息越多意味着均方误差越小. 特例 G = { ∅ , Ω } \mathcal{G}= \{\emptyset, \Omega\} G={∅,Ω}.
习题 4.1.6. 子 σ \sigma σ代数越大, 条件期望的误差越小 如果 G ⊂ F \mathcal{G} \subset \mathcal{F} G⊂F, E X 2 < ∞ E X^{2}<\infty EX2<∞,则
E ( { X − E ( X ∣ F ) } 2 ) + E ( { E ( X ∣ F ) − E ( X ∣ G ) } 2 ) = E ( { X − E ( X ∣ G ) } 2 ) E\left(\{X-E(X \mid \mathcal{F})\}^{2}\right)+E\left(\{E(X \mid \mathcal{F})-E(X \mid \mathcal{G})\}^{2}\right)=E\left(\{X-E(X \mid \mathcal{G})\}^{2}\right) E({X−E(X∣F)}2)+E({E(X∣F)−E(X∣G)}2)=E({X−E(X∣G)}2)
证明:(i) 令 Z Z Z是 L 2 ( F ) L^{2}(\mathcal{F}) L2(F)上的任意点,由定理4.1.14可得
E ( X − Y ) 2 = E { X − E ( X ∣ F ) + Z } 2 = E { X − E ( X ∣ F ) } 2 + E Z 2 E(X-Y)^{2}=E\{X-E(X \mid \mathcal{F})+Z\}^{2}=E\{X-E(X \mid \mathcal{F})\}^{2}+E Z^{2} E(X−Y)2=E{X−E(X∣F)+Z}2=E{X−E(X∣F)}2+EZ2
当 Z = 0 Z=0 Z=0,可以最小化 E ( X − Y ) 2 E(X-Y)^{2} E(X−Y)2.
(ii)在定理4.1.15中, 令 Z = E ( X ∣ F ) − E ( X ∣ G ) ∈ F Z=E(X \mid \mathcal{F})-E(X \mid \mathcal{G}) \in \mathcal{F} Z=E(X∣F)−E(X∣G)∈F.
习题 4.1.9-4.1.10. E ( Y ∣ G ) E(Y \mid \mathcal{G}) E(Y∣G), Y Y Y几乎处处相等的条件
(i) E Y 2 = E [ E ( Y ∣ G ) ] 2 < ∞ E Y^{2}=E [E(Y \mid \mathcal{G})]^{2}<\infty EY2=E[E(Y∣G)]2<∞, 则 E ( Y ∣ G ) = Y E(Y \mid \mathcal{G})=Y E(Y∣G)=Y a.s.;
(ii) E Y 2 < ∞ E Y^{2}<\infty EY2<∞, E ( Y ∣ G ) E(Y \mid \mathcal{G}) E(Y∣G)与 Y Y Y有相同分布, 则 E ( Y ∣ G ) = Y E(Y \mid \mathcal{G})=Y E(Y∣G)=Y a.s.;
(iii) E ∣ Y ∣ < ∞ E|Y|<\infty E∣Y∣<∞, E ( Y ∣ G ) E(Y \mid \mathcal{G}) E(Y∣G)与 Y Y Y有相同分布, 则 E ( Y ∣ G ) = Y E(Y \mid \mathcal{G})=Y E(Y∣G)=Y a.s.
证明:(i) 在习题4.1.6中令 G = { ∅ , Ω } \mathcal{G}=\{\emptyset, \Omega\} G={∅,Ω}可证;
(ii) E ( Y ∣ G ) E(Y \mid \mathcal{G}) E(Y∣G)与 Y Y Y有相同分布, 自然 E Y 2 = E X 2 < ∞ E Y^{2}=E X^{2}<\infty EY2=EX2<∞, 由(i)可证;
(iii) 令 X = Y − c X=Y-c X=Y−c, 由Jensen不等式和 E ( Y ∣ G ) E(Y \mid \mathcal{G}) E(Y∣G)与 Y Y Y有相同分布, 可得 E ( ∥ X ∥ G ) = E ( X ∣ G ) E(\| X \| \mathcal{G})=E(X \mid \mathcal{G}) E(∥X∥G)=E(X∣G) a.s. on { E ( X ∣ G ) > 0 } \{E(X \mid \mathcal{G})>0\} {E(X∣G)>0}. 故
sgn ( X ) = sgn ( E ( X ∣ G ) ) , a . s . \operatorname{sgn}(X)=\operatorname{sgn}(E(X \mid \mathcal{G})),a.s. sgn(X)=sgn(E(X∣G)),a.s.. 由 c c c的任意性可证.
习题 4.1.7-4.1.8 随机个随机变量求和的方差公式 定义条件方差 v a r ( X ∣ F ) = E ( X 2 ∣ F ) − E ( X ∣ F ) 2 {var}(X \mid \mathcal{F})=E\left(X^{2} \mid \mathcal{F}\right)-E(X \mid \mathcal{F})^{2} var(X∣F)=E(X2∣F)−E(X∣F)2. 则
- (i) v a r ( X ) = E ( v a r ( X ∣ F ) ) + v a r ( E ( X ∣ F ) ) {var}(X)=E({var}(X \mid \mathcal{F}))+{var}(E(X \mid \mathcal{F})) var(X)=E(var(X∣F))+var(E(X∣F)).
- (ii) 令 Y 1 , Y 2 , … Y_{1}, Y_{2}, \ldots Y1,Y2,…i.i.d,期望 μ \mu μ,方差 σ 2 , N \sigma^{2}, N σ2,N是独立正整数值的随机变量, E N 2 < ∞ E N^{2}<\infty EN2<∞, 且 X = Y 1 + ⋯ + Y N X=Y_{1}+\cdots+Y_{N} X=Y1+⋯+YN, 则 v a r ( X ) = σ 2 E N + μ 2 v a r ( N ) {var}(X)=\sigma^{2} E N+\mu^{2} {var}(N) var(X)=σ2EN+μ2var(N).
证明:(i) 直接计算; (ii) 利用(i)直接计算即可.
4. 正则条件概率
初等概率论中,我们知道条件期望可以写为条件概率的积分,因此我们现在的问题是 E ( X ∣ F ) = ∫ X μ ( w , d x ) \mathbf{E}(X \mid \mathcal{F})=\int X {\mu}\left(w,dx\right) E(X∣F)=∫Xμ(w,dx)是否成立. 因此, 需要满足两个条件: ( i ) (i) (i) 对每个 ω ∈ Ω \omega \in \Omega ω∈Ω, 上式关于 F \mathcal{F} F可测; ( i i ) (ii) (ii) 为了保证可积性,对 ∀ A ∈ σ ( X ) \forall A \in \sigma(X) ∀A∈σ(X), 要求 P ( A ∣ F ) \mathbf{P}(A \mid \mathcal{F}) P(A∣F) 是概率测度. 这就直接给出了正则条件概率的定义.
但是满足这两个条件比想象中的复杂. 可以证明条件概率 P ( A ∣ G ) P(A \mid \mathscr{G}) P(A∣G)并不总是满足条件. 例如 A 1 , A 2 , … A_{1}, A_{2}, \ldots A1,A2,…互不相交, 虽然有
P ( X ∈ ∪ n A n ∣ G ) = ∑ n P ( X ∈ A n ∣ G ) a.s. P\left(X \in \cup_{n} A_{n} \mid \mathcal{G}\right)=\sum_{n} P\left(X \in A_{n} \mid \mathcal{G}\right) \quad \text { a.s. } P(X∈∪nAn∣G)=n∑P(X∈An∣G) a.s.
但是如果 S \mathcal{S} S包含足够多可数的不相交集合,例外集(exceptional sets)可能会堆积起来.
换句话说, 对于 ∀ A ∈ σ ( X ) \forall A \in \sigma(X) ∀A∈σ(X), 都存在 N A N_{A} NA 是一个关于 A A A 的零测集, 使得在 N A N_{A} NA 上 P ( A ∣ G ) \mathbf{P}(A \mid \mathcal{G}) P(A∣G)可能不是概率测度. 取遍 σ ( X ) \sigma(X) σ(X) 上所有的集合,这些不满足的零测集集合起来不一定还是零测集, 这意味着对每个 ω ∈ Ω \omega \in \Omega ω∈Ω不一定都是概率测度.
正则条件概率 令 ( Ω , F , P ) (\Omega, \mathcal{F}, P) (Ω,F,P)是概率空间, X : ( Ω , F ) → ( S , S ) X:(\Omega, \mathcal{F}) \rightarrow(S, \mathcal{S}) X:(Ω,F)→(S,S)是可测映射, σ \sigma σ代数 G ⊂ F . μ : Ω × S → [ 0 , 1 ] \mathcal{G} \subset \mathcal{F} . \mu: \Omega \times \mathcal{S} \rightarrow[0,1] G⊂F.μ:Ω×S→[0,1]被称为是给定 G \mathcal{G} G下 X X X的正则条件概率, 如果
- (i) 对于每个 A ⊂ S , ω → μ ( ω , A ) A\subset S, \omega \rightarrow \mu(\omega, A) A⊂S,ω→μ(ω,A)是 P ( X ∈ A ∣ G ) P(X \in A \mid \mathcal{G}) P(X∈A∣G)的一个版本.
- (ii) 对于几乎每个 ω ∈ Ω , A → μ ( ω , A ) \omega\in \Omega, A \rightarrow \mu(\omega, A) ω∈Ω,A→μ(ω,A)是 ( S , S ) (S, \mathcal{S}) (S,S)上的概率测度.
当 S = Ω S=\Omega S=Ω, X X X是到自身的映射, μ \mu μ被称为正则条件概率.
示例. “给定随机变量的条件概率"是正则条件概率 假设 X X X, Y Y Y有联合密度 f ( x , y ) > 0 f(x, y)>0 f(x,y)>0. 如果 μ ( y , A ) = ∫ A f ( x , y ) d x / ∫ f ( x , y ) d x \mu(y, A)=\int_{A} f(x, y) d x / \int f(x, y) d x μ(y,A)=∫Af(x,y)dx/∫f(x,y)dx
则 μ ( Y ( ω ) , A ) \mu(Y(\omega), A) μ(Y(ω),A)是给定 σ ( Y ) \sigma(Y) σ(Y)下 X X X的正则条件概率.
证明:验证正则条件概率的两个条件, (i) 在示例 4.1.6(条件期望的公式)的定义中取 g = 1 A g=1_{A} g=1A; (ii) 控制收敛定理意味着 A → μ ( y , A ) A \rightarrow \mu(y, A) A→μ(y,A)是概率测度.
定理 4.1.16. 条件期望是关于正则条件概率的积分 令 μ ( ω , A ) \mu(\omega, A) μ(ω,A)是正则条件概率,对于 X X X给定 F . \mathcal{F} . F.如果 f : ( S , S ) → ( R , R ) f:(S, \mathcal{S}) \rightarrow (\mathbf{R}, \mathcal{R}) f:(S,S)→(R,R)满足 E ∣ f ( X ) ∣ < ∞ E|f(X)|<\infty E∣f(X)∣<∞,则
E ( f ( X ) ∣ F ) = ∫ μ ( ω , d x ) f ( x ) . a . s . E(f(X) \mid \mathcal{F})=\int \mu(\omega, d x) f(x).a.s. E(f(X)∣F)=∫μ(ω,dx)f(x).a.s..
证明:对于示性函数 f = 1 A f=1_A f=1A,只需证明 E [ 1 A ∣ F ] = ∫ A μ ( ω , d x ) E[1_A|\mathcal{F}]=\int_A\mu(\omega,dx) E[1A∣F]=∫Aμ(ω,dx), 根据定义 P ( A ∣ F ) = μ ( ω , A ) P(A|\mathcal{F})=\mu(\omega,A) P(A∣F)=μ(ω,A), 上式显然成立. 分步依次证明简单函数,非负函数,一般函数.
本节考虑随机变量取值于nice空间的正则条件概率, 其中 nice空间是指存在1-1映射 φ : S → R \varphi: S \rightarrow \mathbf{R} φ:S→R使得 φ \varphi φ和 φ − 1 \varphi^{-1} φ−1可测的空间.
定理 4.1.17 取值nice空间, 存在给定 G \mathcal{G} G下正则条件概率 若 X X X, Y Y Y取值于nice空间 ( S , S ) (S, \mathcal{S}) (S,S)和 G = σ ( Y ) \mathcal{G}=\sigma(Y) G=σ(Y). 存在函数 μ : Ω o × S → [ 0 , 1 ] \mu: \Omega_{o} \times \mathcal{S} \rightarrow[0,1] μ:Ωo×S→[0,1]使得\
- (i) 对每个 A , μ ( ω , A ) A, \mu(\omega, A) A,μ(ω,A)是 P ( X ∈ A ∣ G ) P(X \in A \mid \mathcal{G}) P(X∈A∣G)的一个版本;\
- (ii) 对几乎每个 ω , A → μ ( ω , A ) \omega, A \rightarrow \mu(\omega, A) ω,A→μ(ω,A)是 ( S , S ) (S, \mathcal{S}) (S,S)上的概率测度.
注释:(1) 考虑 ϕ X \phi{X} ϕX. 先证明有一个版本为 P ( φ ( X ) ≤ q ∣ G ) P(\varphi(X) \leq q \mid \mathcal{G}) P(φ(X)≤q∣G)的 ω → G ( q , ω ) , q ∈ Q \omega \rightarrow G(q, \omega), q\in Q ω→G(q,ω),q∈Q的存在性, 由于 q ∈ Q q\in Q q∈Q, 容易验证可列可加性; 利用条件期望的单调收敛定理可以证明一个版本为 P ( φ ( X ) ≤ x ∣ G ) P(\varphi(X) \leq x \mid \mathcal{G}) P(φ(X)≤x∣G)的分布函数 F ( x , ω ) F(x, \omega) F(x,ω)的存在性; 由此可得测度 v v v的存在性, 验证每个 B ∈ R , ν ( ω , B ) B \in \mathcal{R}, \nu(\omega, B) B∈R,ν(ω,B)是 P ( φ ( X ) ∈ B ∣ G ) P(\varphi(X) \in B \mid \mathcal{G}) P(φ(X)∈B∣G)的一个版本,(2) 回到 X X X. 可以证明 μ ( ω , A ) = ν ( ω , B ) \mu(\omega, A)=\nu(\omega, B) μ(ω,A)=ν(ω,B), 满足条件(i)(ii).
证明: (1) 利用条件期望的单调性并且摒弃可数个空集,可以发现存在集合 Ω o \Omega_{o} Ωo使得 P ( Ω o ) = 1 P\left(\Omega_{o}\right)=1 P(Ωo)=1,并且一族随机变量 G ( q , ω ) , q ∈ Q G(q, \omega), q \in \mathbf{Q} G(q,ω),q∈Q使得 q → G ( q , ω ) q \rightarrow G(q, \omega) q→G(q,ω)是不减的, ω → G ( q , ω ) \omega \rightarrow G(q, \omega) ω→G(q,ω)是 P ( φ ( X ) ≤ q ∣ G ) P(\varphi(X) \leq q \mid \mathcal{G}) P(φ(X)≤q∣G)的一个版本.
(2) 令 F ( x , ω ) = inf { G ( q , ω ) : q > x } F(x, \omega)=\inf \{G(q, \omega): q>x\} F(x,ω)=inf{G(q,ω):q>x}.
由定理3.2.12得 F F F是分布函数. G ( q n , ω ) ↓ F ( x , ω ) G\left(q_{n}, \omega\right) \downarrow F(x, \omega) G(qn,ω)↓F(x,ω), 条件期望的单调收敛定理得 F ( x , ω ) F(x, \omega) F(x,ω)是 P ( φ ( X ) ≤ x ∣ G ) P(\varphi(X) \leq x \mid \mathcal{G}) P(φ(X)≤x∣G)的一个版本.
(3) 对于每个 ω ∈ Ω o \omega \in \Omega_{o} ω∈Ωo, 存在 ( R , R ) (\mathbf{R}, \mathcal{R}) (R,R)上的唯一测度 ν ( ω , ⋅ ) \nu(\omega, \cdot) ν(ω,⋅)使得 $\nu(\omega,(-\infty, x])=F(x, \omega) $. 为验证每个 B ∈ R , ν ( ω , B ) B \in \mathcal{R}, \nu(\omega, B) B∈R,ν(ω,B)是 P ( φ ( X ) ∈ B ∣ G ) P(\varphi(X) \in B \mid \mathcal{G}) P(φ(X)∈B∣G)的一个版本, 可以看到这个表述是正确的 B B B类(包括 ω → ν ( ω , B ) \omega \rightarrow \nu(\omega, B) ω→ν(ω,B)的可测性 ) 是 λ \lambda λ类,包括所有具有形式 ( a 1 , b 1 ] ∪ ⋯ ( a k , b k ] \left(a_{1}, b_{1}\right] \cup \cdots\left(a_{k}, b_{k}\right] (a1,b1]∪⋯(ak,bk]的集合,其中 − ∞ ≤ a i < b i ≤ ∞ -\infty \leq a_{i}<b_{i} \leq \infty −∞≤ai<bi≤∞,
因此由 π − λ \pi-\lambda π−λ 定理可得结论成立.
根据nice空间的定义,存在1-1 映射 φ : S → R \varphi: S \rightarrow \mathbf{R} φ:S→R使得 φ \varphi φ, φ − 1 \varphi^{-1} φ−1可测. 如果 A ∈ S A \in \mathcal{S} A∈S, B = φ ( A ) B=\varphi(A) B=φ(A), 则 B = ( φ − 1 ) − 1 ( A ) ∈ R B=\left(\varphi^{-1}\right)^{-1}(A) \in \mathcal{R} B=(φ−1)−1(A)∈R, 并且 μ ( ω , A ) = ν ( ω , B ) \mu(\omega, A)=\nu(\omega, B) μ(ω,A)=ν(ω,B).
定理 4.1.18 取值nice空间且 G = σ ( Y ) \mathcal{G}=\sigma(Y) G=σ(Y), 存在正则条件概率 若 X X X, Y Y Y取值于nice空间 ( S , S ) (S, \mathcal{S}) (S,S)和 G = σ ( Y ) \mathcal{G}=\sigma(Y) G=σ(Y). 存在函数 μ : S × S → [ 0 , 1 ] \mu: S \times \mathcal{S} \rightarrow[0,1] μ:S×S→[0,1]使得
- (i) 对每个 A , μ ( Y ( ω ) , A ) A, \mu(Y(\omega), A) A,μ(Y(ω),A)是 P ( X ∈ A ∣ G ) P(X \in A \mid \mathcal{G}) P(X∈A∣G)的一个版本;
- (ii) 对几乎每个 ω , A → μ ( Y ( ω ) , A ) \omega, A \rightarrow \mu(Y(\omega), A) ω,A→μ(Y(ω),A)是 ( S , S ) (S, \mathcal{S}) (S,S)上的概率测度.
对照定理4.1.17的证明.
证明:(1) 由于 G ( q , ω ) ∈ σ ( Y ) G(q, \omega) \in \sigma(Y) G(q,ω)∈σ(Y), 可以令 G ( q , ω ) = H ( q , Y ( ω ) ) G(q, \omega)=H(q, Y(\omega)) G(q,ω)=H(q,Y(ω)).
(2) 令 F ( x , y ) = inf { G ( q , y ) : q > x } F(x, y)=\inf \{G(q, y): q>x\} F(x,y)=inf{G(q,y):q>x}. 存在集合 A 0 A_{0} A0, P ( Y ∈ A 0 ) = 1 P\left(Y \in A_{0}\right)=1 P(Y∈A0)=1使得当 y ∈ A 0 , F y \in A_{0}, F y∈A0,F 是一个分布函数, F ( x , Y ( ω ) ) F(x, Y(\omega)) F(x,Y(ω))是 P ( φ ( X ) ≤ x ∣ Y ) P(\varphi(X) \leq x \mid Y) P(φ(X)≤x∣Y)的一个版本.
对于每个 y ∈ A o y \in A_{o} y∈Ao, 存在 ( R , R ) (\mathbf{R}, \mathcal{R}) (R,R)上唯一测度 ν ( y , ⋅ ) \nu(y, \cdot) ν(y,⋅)使得 ν ( y , ( − ∞ , x ] ) = F ( x , y ) ) \nu(y,(-\infty, x])=F(x, y)) ν(y,(−∞,x])=F(x,y)). 为验证每个 B ∈ R , ν ( Y ( ω ) , B ) B \in \mathcal{R}, \nu(Y(\omega), B) B∈R,ν(Y(ω),B)是
P ( φ ( X ) ∈ B ∣ Y ) P(\varphi(X) \in B \mid Y) P(φ(X)∈B∣Y)
的一个版本, 上述条件成立的 B B B的集类 (可得 ω → ν ( Y ( ω ) , B ) \omega \rightarrow \nu(Y(\omega), B) ω→ν(Y(ω),B)可测 ) 是一个 λ \lambda λ-类, 包含形式为 ( a 1 , b 1 ] ∪ ⋯ ( a k , b k ] \left(a_{1}, b_{1}\right] \cup \cdots\left(a_{k}, b_{k}\right] (a1,b1]∪⋯(ak,bk]的集类, 其中 − ∞ ≤ a i < b i ≤ ∞ -\infty \leq a_{i}<b_{i} \leq \infty −∞≤ai<bi≤∞,
由 π − λ \pi-\lambda π−λ定理可证.
如果 A ∈ S A \in \mathcal{S} A∈S, B = φ ( A ) B=\varphi(A) B=φ(A) 则 B = ( φ − 1 ) − 1 ( A ) ∈ R B=\left(\varphi^{-1}\right)^{-1}(A) \in \mathcal{R} B=(φ−1)−1(A)∈R, 令 μ ( y , A ) = ν ( y , B ) \mu(y, A)=\nu(y, B) μ(y,A)=ν(y,B), 可得正则条件概率的存在性.