算法学习笔记（3）-差分-编程知识

#差分

差分和前缀和互为逆运算：

给定一个原数组s，差分数组h，两者的关系如下所示：

s[i] = h[1] + h[2] + h[3] + …… +h[i]

针对于上面的公式，由差分数组h推导而来

h[1] = s[1]

h[2] = s[2] - s[1]

h[3] = s[3] - [2]

……

h[n] = s[n] - s[n-1]

将上述公式加起来接得到了：s[i] = h[1] + h[2] + h[3] + …… +h[i]

因此原数组s是差分数组h的前缀和，差分数组h为原数组s的差分。

差分的用途：

构造一个数组的差分矩阵（差分数组），是为了针对频繁的对数组中某个区间进行同一操作。

示例：

将序列中[l,r]之间的每一个数加上c这一操作，可以执行n次，每次的c都不相同，如果直接对原数组进行操作，每次操作都会花费O(n)的时间复杂度，总体的时间复杂度就变成了O(n^2)。但是如果使用该数组的差分矩阵（差分数组）进行操作，会将每一次的操作的时间复杂度降为O(1)，整体的时间复杂度就变成了O(n)，说白了利用了一种特殊的数学性质，利用空间来换时间。然后根据前缀和和差分就能得到具体的答案。

#一维差分

所谓的一维差分就是在我们已有一维数组的基础上构造一个差分数组，此时差分数组需要初始化操作，时间复杂度O(n);

具体的代码示例：

//c++基础差分示例代码
h[0] = s[0]
for (int i = 1 ; i < n ; i++){h[i] = s[i] - s[i-1] ;}//c++可以边获取元素边进行差分操作
int n,m,s[100005],h[100005] ;
//差分操作-对一个区间进行操作
void Add(int c , int l , int r)
{h[l] += c ;h[r+1] -= c ;
}
int main()
{
scanf("%d %d",&n,&m) ;
//初始化差分数组for (int i = 1 ; i <= n ; i++)
{scanf("%d",&s[i]) ;Add(s[i],i,i) ;
}
//详细说明一下这个初始化操作的过程-我们初始化是从1 - n,闭区间进行的操作
// s[1] , h[1] += s[1] , h[2] -= s[1] ,                 h[1] = s[1]
// s[2] , h[2] += s[2] , h[3] -= s[2] ,第一个差分出来了, h[2] = s[2] - s[1]
// s[3] , h[3] += s[3] , h[4} -= s[3] ,第二个差分出来了, h[3] = s[3] - s[2]
//以此类推                                              h[n] = s[n] - s[n-1]
}

//python代码示例-1
s = [0] * 100005
h = [0] * 100005//差分操作-对一个区间进行操作
def add(c , l , r)h[l] += c h[r+1] -= c n,m = map(int,input().split())for i in range(1,n):s[i] = int(input())add(s[i],i,i)//python代码示例-2
s = [map(int,input().split())]
h = [0] * len(s)
h[0] = s[0]
for i in range(1,n) :h[i] = s[i] - s[i - 1]

恢复操作完成的数组-采用前缀和进行恢复-二者互为逆运算：

具体的代码示例：
//c++代码示例-利用前缀和来进行恢复，二者互为逆运算
for (int i = 1 ; i < n ; i++)
{h[i] += h[i-1] ;printf("%d",h[i]) ;
}
#python代码示例
for i in range(1,n) :h[i] += h[i-1]print(h[i])

##实战演练

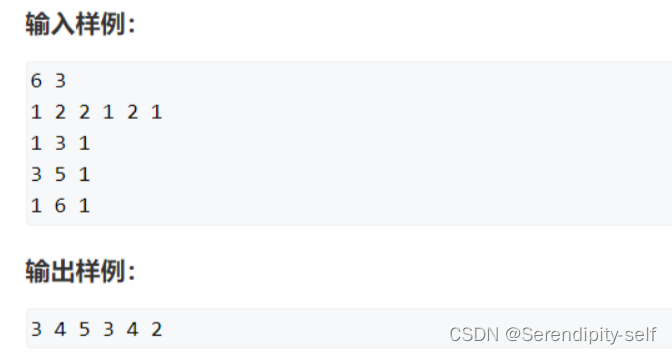
//c++代码示例
#include <iostream>
using namespace std ;const int N = 100001 ;
int n,m ;
int s[N],h[N] ;void add(int c,int l,int r)
{h[l] += c ;h[r+1] -= c ;
}
//示例1
int main()
{scanf("%d%d",n,m) ;for (int i = 1 ; i <= n ; i++){scanf("%d",&s[i]) ;}for (int i = 1 ; i<= n ; i++){add(s[i],i,i) ;}while (m--){int l,r,c ;scanf("%d%d%",&l,&r,&c) ;add(c,l,r) ;}for (int i = 1 ; i<= n ; i++){h[i] += h[i-1] ;printf("%d ",h[i]) ;}return 0 ;
}
//示例2
int main()
{cin >> n >> m ;for (int i = 1 ; i<=n ; i++){cin >> s[i] ;h[i] = h[i] - h[i-1] ;}while (m--){int l,r,c ;cin >> l >> r >> c ;h[l] += c ;h[r+1} -= c ;}for (int i = 1 ; i <= n ; i++){h[i] = h[i] + h[i - 1] ;cout << h[i] << " " ;}return 0 ;
}

//python代码示例n,m = map(int,input().split())s = [map(int,input().split())]
h = [0] * (len(s))
h[0] = s[0]for i in range(1,n):h[i] = h[i] - h[i-1]for _ in range(m):l,r,c = map(int,input().split())h[l] += ch[r+1] -= cfor i in range(1,n):h[i] = h[i] + h[i - 1]print(h[i],end = " ")

#二维差分

所谓的二维差分就类似在二维数组进行一个数值更新的过程，你也可以理解成为由上一步的结果推导出来下一步的结果。

具体的操作是选取了一块区域进行操作，因此在考虑区域更改，就要考虑方向性问题：

1.差分数组的更新过程
//c++示例代码
void insert(int x1, int y1, int x2,int y2)
{h[x1][y1] += c ;h[x2+1][y1] -= c ;h[x1][y2+1] -= c ;h[x2+1][y2+1] += c ;
}
#python代码示例
def void(x1,y1,x2,y2) :h[x1][y1] += c h[x2+1][y1] -= c h[x1][y2+1] -= c h[x2+1][y2+1] += c 
2.差分数组初始化
//c++代码
for (int i = 1 ; i <= n ; i++)
{for (int j = 1 ; j <= n ; j++){insert(i,j,i,j,s[i][j]) ;}
}
#python代码示例
for i in range(1,n+1):for j in range(1,n+1):insert(i,j,i,j,s[i][j)
3.对结果的恢复-逆运算求前缀和
//c++代码示例
for (int i = 1 ; i <= n ; i++)
{for (int j = 1 ; j <= n ; j++){h[i][j] += h[i-1][j] + h[i][j-1] + h[i-1][j-1] ;print("%d",h[i][j]) ;}puts("") ;
}
//python代码示例
for i in range(1,n+1):for j in range(1,n+1):h[i][j] += h[i-1][j] + h[i][j-1] + h[i-1][j-1]print(h[i][j],end=" ")print()

##实战演练

##代码示例

//c++代码示例
#include <iostream>
using namespace std ;const int N = 1010 ;
int n,m,q ;
int s[N][N],h[N][N] ;void insert(int x1, int y1, int x2, int y2, int c)
{h[x1][y1] += c ;h[x2+1][y1] -= c ;h[x1][y2+1] -= c ;h[x2+1][y2+1] += c ;
} int main()
{scanf("%d%d%",&n,&m,&q) ;for (int i = 1 ; i <= n ; i++){for (int j = 1 ; j <= m ; j++){scanf("%d",&s[i][j]) ;}}for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){insert(i,j,i,j,s[i][j]);}}while (q--){   int x1,x2,y1,y2,c ;cin >> x1 >> y1 >> x2 >> y2 >> c ;insert(x1,y1,x2,y2,c) ;}for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){h[i][j] += h[i-1][j] + h[i][j-1] - h[i-1][j-1];}}for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){printf("%d ",h[i][j]);}puts("");}   return 0;}

#python代码示例def insert(x1, y1, x2, y2, c):h[x1][y1] += ch[x2 + 1][y1] -= ch[x1][y2 + 1] -= ch[x2 + 1][y2 + 1] += cn, m, q = map(int, input().split())
h = [[0] * (m+2) for _ in range(n+2)]
mp = [[0] * (m+2)]
# print(mp)
for _ in range(n):mp.append([0] + list(map(int,input().split())) + [0])
# print(mp)for i in range(1, n+1):for j in range(1, m+1):insert(i, j, i, j, mp[i][j])for _ in range(q):x1,y1,x2,y2,c = map(int , input().split())insert(x1, y1, x2, y2, c)for i in range(1, n+1):for j in range(1, m+1):h[i][j] += h[i - 1][j] + h[i][j - 1] - h[i - 1][j - 1]
# print(h)
for i in range(1,n+1):for j in range(1,m+1):print(h[i][j], end=" ")print()