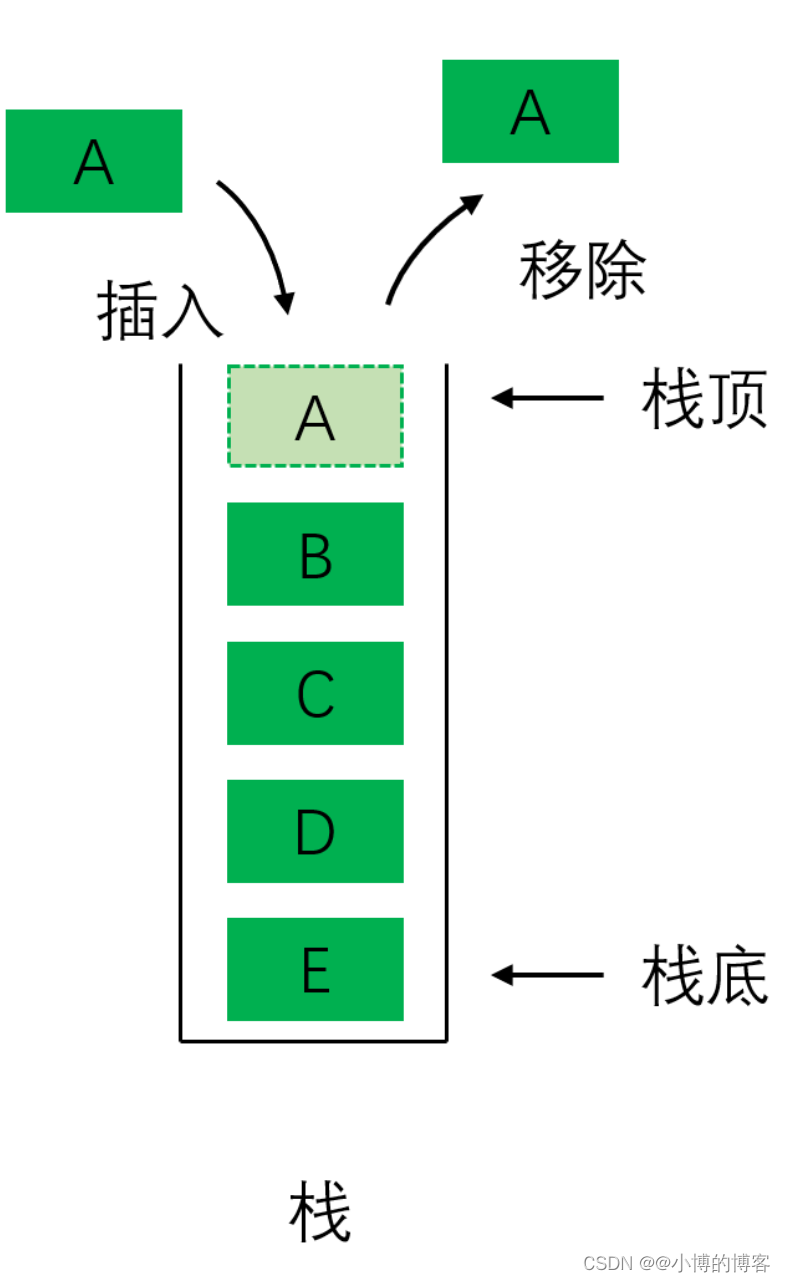
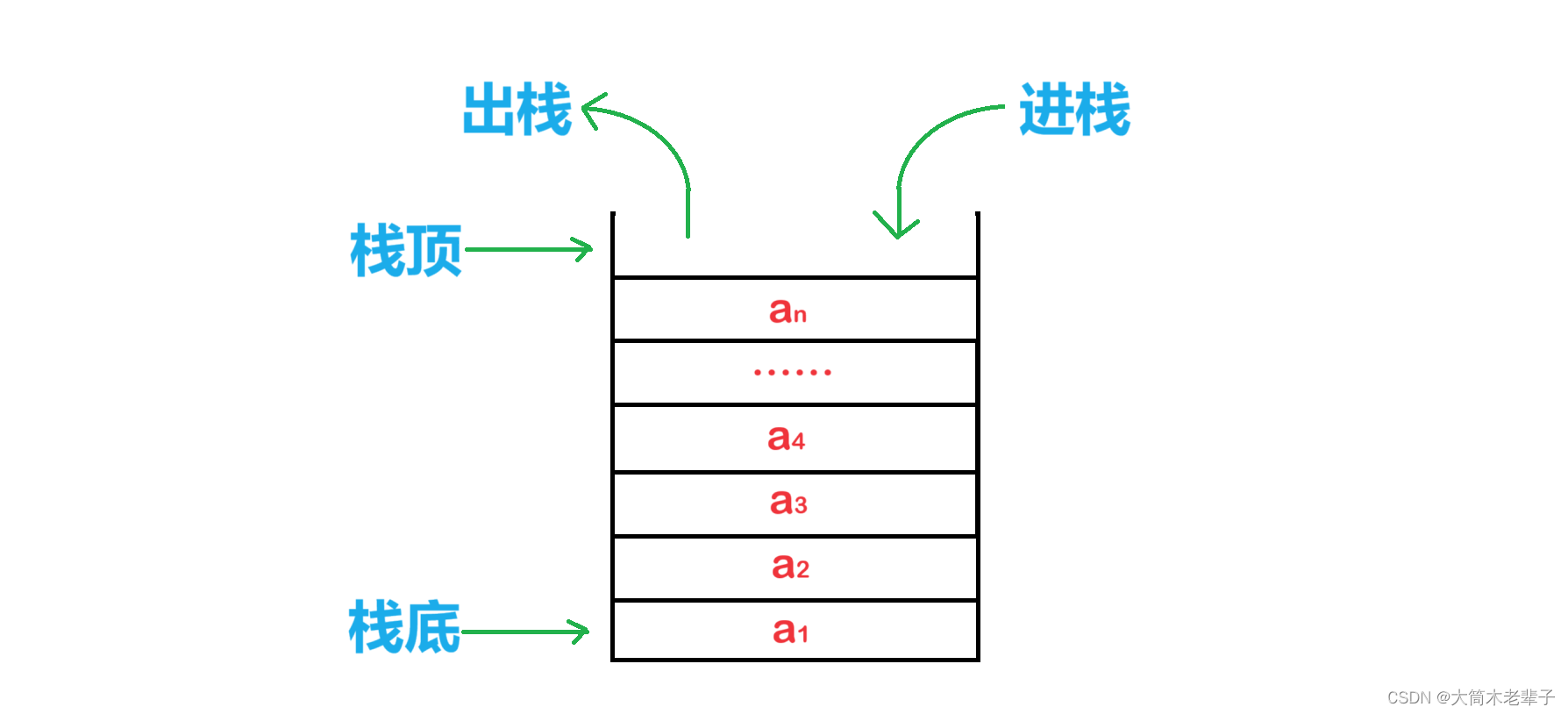
static Range Max/Min Query
ST表
利用的是动态规划的思想
状态:
//st[i][j]-->区间长度为1<<j,在区间[i,i+1<<j-1]上的最值状态转移方程:
st[i][j]=max(st[i][j-1],st[i+(1<<j-1)][j-1]);
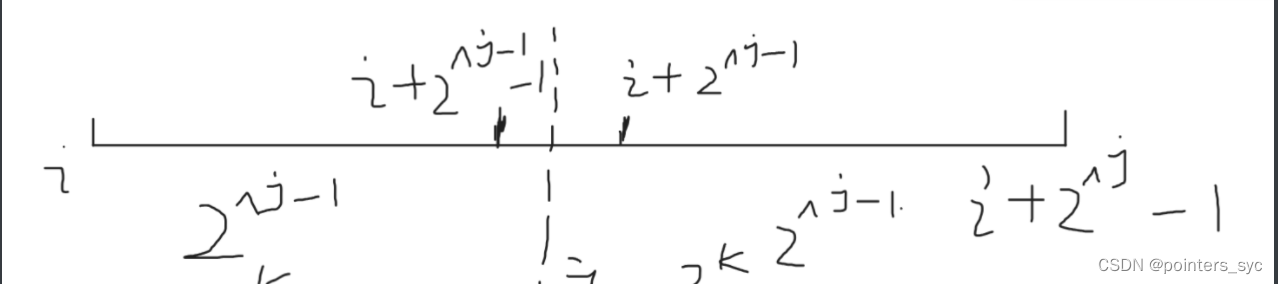
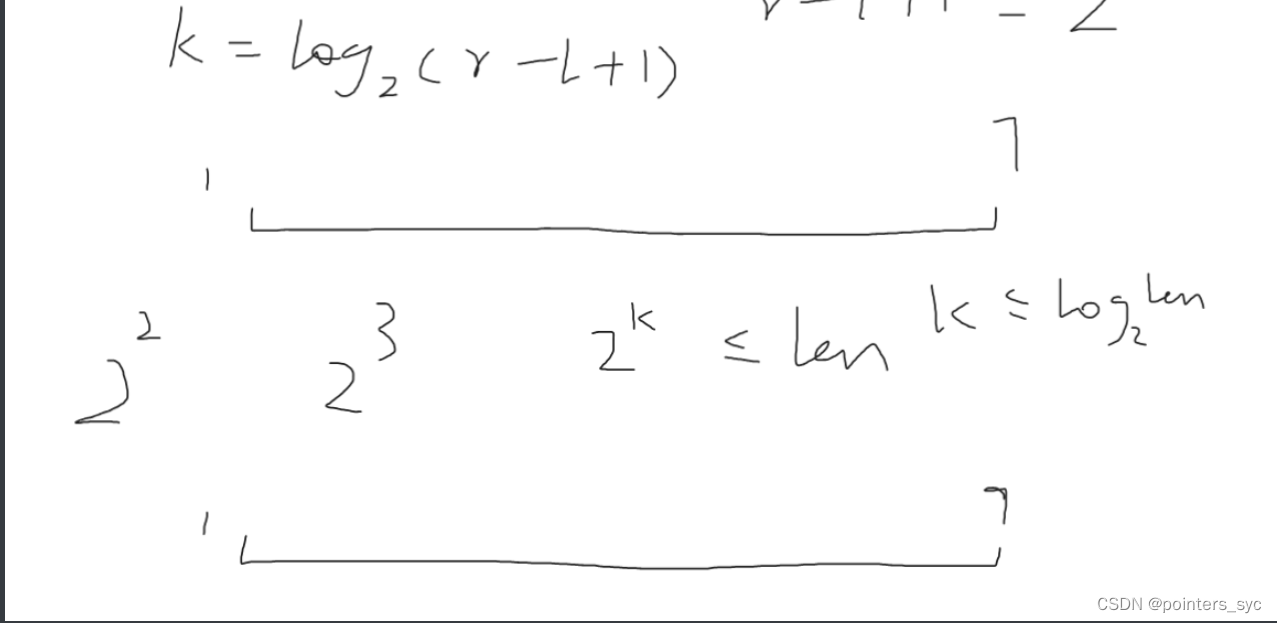
#include <iostream>
#include <cmath>using namespace std;
const int N=1e5+10;
int n,T,a[N],st[N][31];
//st[i][j]-->区间长度为1<<j,在区间[i,i+1<<j-1]上的最值
//st[i][j]=max(st[i][j-1],st[i+(1<<j-1)][j-1]); //创建st表时间复杂度为O(nlogn)
void createST(){//先给倍增区间的st[i][j]赋值for(int j=1;j<=log2(n);j++){//外层必须是区间长度,因为只有把区间长度为1的都算了,才能二分着算区间长度为2的 for(int i=1;i+(1<<j)-1<=n;i++){st[i][j]=max(st[i][j-1],st[i+(1<<j-1)][j-1]); }}
}
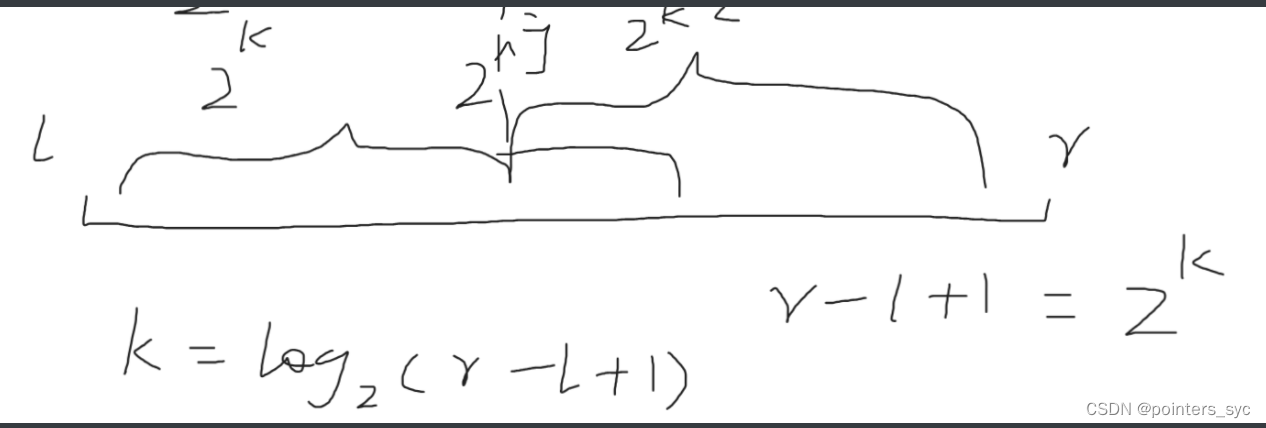
//查询时间复杂度为O(1)
int query(int l,int r){//1<<k为最小交叉区间 int k=log2(r-l+1);return max(st[l][k],st[r+1-(1<<k)][k]);
}
int main(){cin>>n>>T;for(int i=1;i<=n;i++){scanf("%d",&a[i]);st[i][0]=a[i];} createST();while(T--){int l,r;scanf("%d %d",&l,&r);printf("%d\n",query(l,r));}return 0;
}