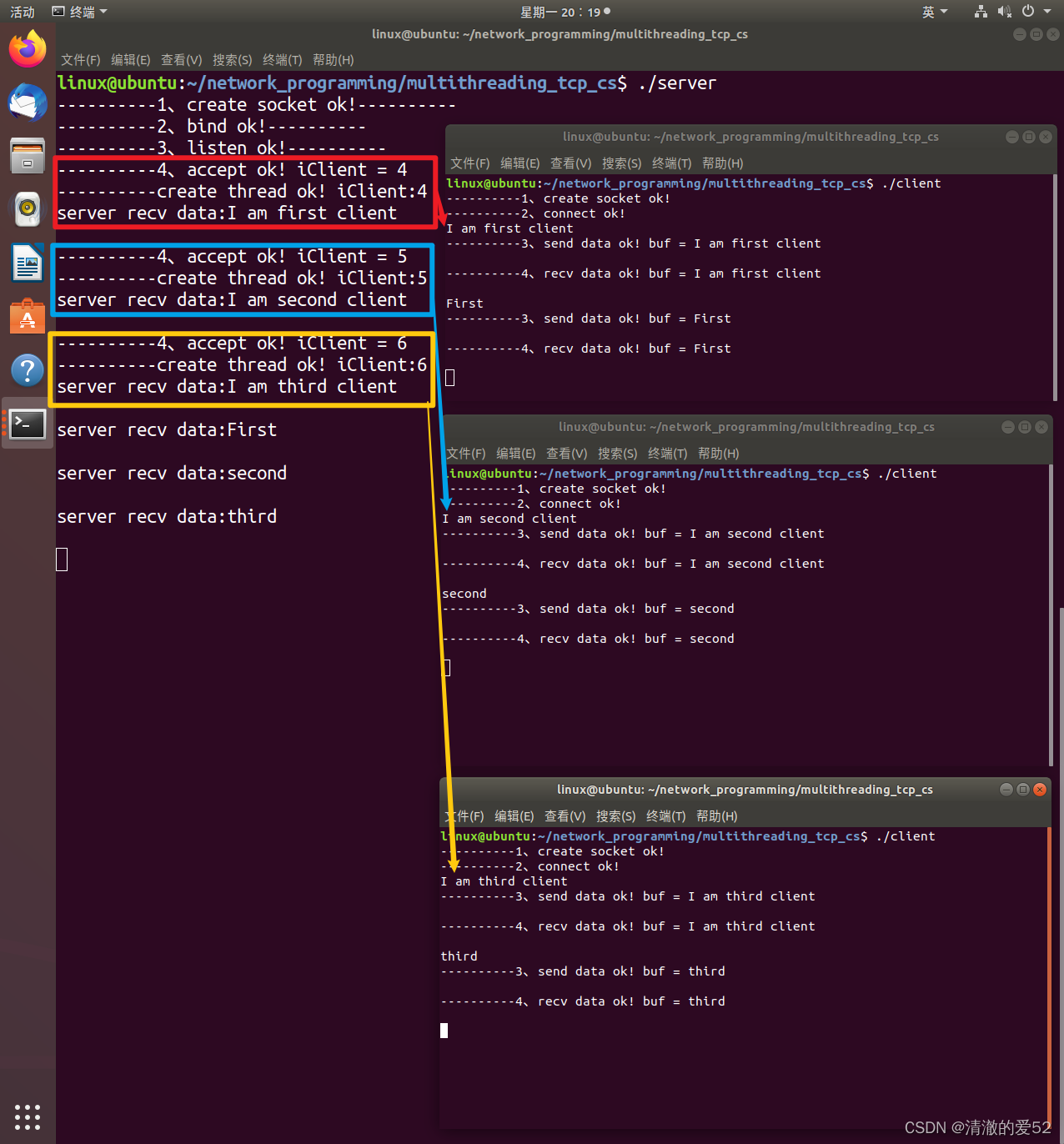
M 有效算法

本题考验二分知识,思路是二分k的取值,就按第一组样例来说当我们k取值为1的时候我们遍历数组想让|8-x|<=k1的话x的取值范围是7-9,想让|3-x|<=k2的话x的取值范围是1-5,两者x的区间不重合,说明肯定没有x能同时让|8-x|<=k1和|3-x|<=k2,所以不成立,当k=2的时候我们发现每一组x的区间都有重合的地方,那么此时a数组一定是可以全都变成x的,并且当k>2时毫无疑问绝对都可以符合,k的取值是否达标具有单调性,所以可以用二分来枚举。
题解如下:
#define _CRT_SECURE_NO_WARNINGS
#include<bits/stdc++.h>
#include<unordered_map>
using namespace std;
#define for1 for(int i = 1;i <= n;i++)
#define for0 for(int i = 0;i < n;i++)
#define forn1 for(int j = 1;j <= n;j++)
#define forn0 for(int j = 0;j < n;j++)
#define form1 for (int j = 1; j <= m; j++)
#define form0 for (int j = 0; j < m; j++)
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define arrn int* arr = new int[n+2];arr[0] = 0,arr[n+1]=0
#define carr cin >> arr[i]
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define endl '\n'
#define mod 1000000007
#define t() int _; cin >> _; while (_--)
int a[300010];
int b[300010];
int n;
bool cheak(int k)
{long long ml = a[1] - 1ll * b[1] * k;long long mr = a[1] + 1ll * b[1] * k;for (int i = 2; i <= n; i++){long long ll = a[i] - 1ll * b[i] * k;long long rr = a[i] + 1ll * b[i] * k;if (ll > ml)ml = ll;if (rr < mr)mr = rr;}if (mr < ml)return false;return true;
}
int main() {IOS;int t;cin >> t;while (t--){cin >> n;for(int i = 1; i <= n; i++)cin >> a[i];for(int i = 1; i <= n; i++)cin >> b[i];int l = 0, r = 1e9;while (l <= r){int mid = (l + r) >> 1;if (cheak(mid))r = mid-1;else l = mid+1;}cout << l << endl;}return 0;
}