原篇：（ACM算法）tarjan算法求LCA - 知乎 (zhihu.com)

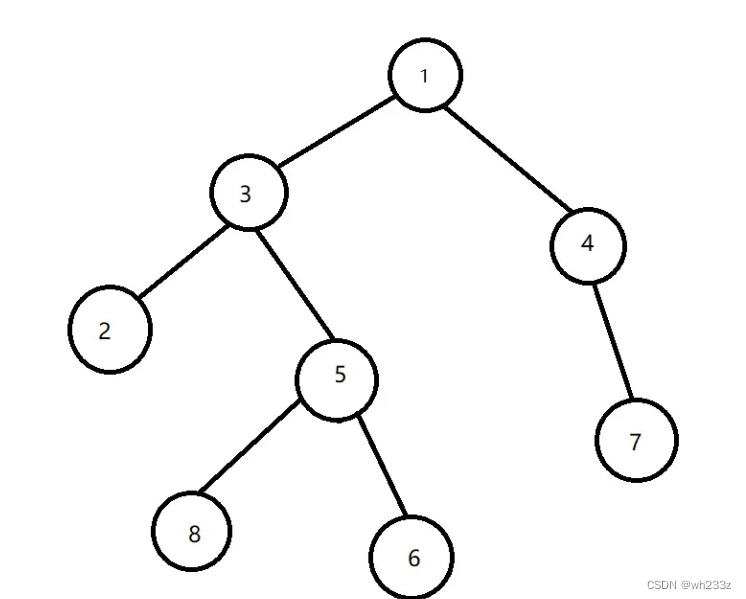
顾名思义，就是求两个节点最近的共同祖先，就好比下图，2和3的共同祖先为3，2和4的共同祖先为1。

关于LCA求解有3种算法。

1.标记回溯法（也称暴力枚举，从一个点开始向上标记他的父节点，直接标记到根节点为止，然后另另一个点也开始向上回溯，当这个点被标记过，则找到这两个点的共同祖先），当数据过大时，很明显这个算法会超时，所以本文不过多解释此方法。

2.ST倍增法（本文也不重点介绍次方法，读者可看其他博客阅读此方法）

3.targan算法（本文重点介绍）

tarjan算法就这几个步骤：
1.标记当前节点x已访问，但是还没有回溯

2.枚举所有没有访问的过的子节点y，继续遍历子节点

3.合并y到x上

4.访问所有与当前节点有询问并且回溯过的y x,y的lca就是find(y)

5.标记当前节点回溯

首先targan是基于并查集实现的，没学过的读者可点击此传送门：何为并查集？-CSDN博客

具体过程看以下代码：

#include<bits/stdc++.h>
#define int long long 
#define endl "\n"
#define fi first
#define se second
#define PII pair<int,int> 
using namespace std;
const int N=5e5+5;
int fa[N],vis[N];
vector<int> v[N];
vector<PII> query[N];
int ans[N]; 
int find(int x){//并查集模板 if(fa[x]==x)  return x;else return fa[x]=find(fa[x]);
}
void tarjan(int x){vis[x]++;//第一次走过的路径标记为1 for(auto i :v[x]){if(!vis[i]){//若子节点没走过 继续遍历子节点 tarjan(i);fa[i]=x;//合并子节点到当前节点 }		}for(auto t : query[x]){int a=t.fi,b=t.se;if(vis[a]==2&&!ans[b]) ans[b]=find(a);// 若已经回溯并且b下标为空 }vis[x]++;//回溯的路径标记为2 
}
void solve(){	int n,m,q;cin >> n >> m >> q;for(int i=1;i<n;++i){int x,y;cin >> x >> y;v[x].push_back(y);//将x，y存入数组中 v[y].push_back(x);}for(int i=1;i<=n;++i) fa[i]=i;//预处理所有节点都是自己的父节点 for(int i=1;i<=m;++i){int x,y;cin >> x >> y;if(x==y){//特判 ans[i]=x;continue;}query[x].push_back({y,i});//存入查询的数字 query[y].push_back({x,i});}tarjan(q);for(int i=1;i<=m;++i){cout << ans[i] << endl;}return ;
}
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;//cin >> t;while(t--) solve();return 0;
}

经典例题：P3884 [JLOI2009] 二叉树问题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

解题思路：用层序遍历的思想求出树的深度和宽度，同时标记每个节点所在的层数，然后用tarjan算法求出a和b的共同祖先，最后套公式输出距离即可。

实现代码：

#include<bits/stdc++.h>
#define int long long 
#define endl "\n"
#define fi first
#define se second
#define PII pair<int,int> 
using namespace std;
const int N=105;
vector<int> v[N];
vector<int> s[N];
queue<PII> q;
int a,b;
int vis[N],fa[N],c[N];
vector<PII> query[N];
int ans1,ans2;
int k;
PII pa;
void check(int x){q.push({1,1});c[1]=1;int sum=0;int t=1;while(!q.empty()){pa=q.front();q.pop();if(pa.se==t) sum++;else{ans2=max(ans2,sum);t++;sum=1;}c[pa.fi]=pa.se;for(int i=0;i<s[pa.fi].size();++i){q.push({s[pa.fi][i],pa.se+1});}} ans1=t;ans2=max(ans2,sum);
}
int find(int x){if(fa[x]==x)  return x;else return fa[x]=find(fa[x]);
}
void tarjan(int x){vis[x]++; for(auto i :v[x]){if(!vis[i]){tarjan(i);fa[i]=x;}		}for(auto t : query[x]){int a=t.fi;if(vis[a]==2){k=find(a);break;} }vis[x]++;
}
void solve(){int n;cin >> n;for(int i=1;i<n;++i){int x,y;cin >> x >> y;v[x].push_back(y);v[y].push_back(x);s[x].push_back(y);}	for(int i=1;i<=n;++i) fa[i]=i; cin >> a >> b;query[a].push_back({b,1});query[b].push_back({a,1});check(1);cout << ans1 << endl << ans2 << endl;tarjan(1);//for(int i=1;i<=n;++i) cout << c[i] << endl; cout << (c[a]-c[k])*2+(c[b]-c[k]);return ;
}
signed main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);int t=1;//cin >> t;while(t--) solve();return 0;
}