交叉链表

. - 力扣(LeetCode)
如果链表的两条链的长度一样,链表两端对齐,解决这个问题将会变得非常简单,直接分别遍历两个链表,想等时的节点即为所求。我们想办法让链表对齐--分别从a和b遍历链表,分别求出以a开始和以b开始时的链表长度,求出a,b之差的绝对值k。然后再让较长一端先走k步,这样就对齐了。然后再同时遍历链表,两端相等时,这个节点即为所求。
其实,这就是一个快慢指针的解法,快慢指针每次都只走一步,只不过快指针先走使链表对齐。
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/typedef struct ListNode ListNode;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {ListNode* a = headA;ListNode* b = headB;int count1 = 0;int count2 = 0;while(a->next){a = a->next;count1++;} while(b->next){b = b->next;count2++;}if (a != b){return NULL;}a = headA;b = headB;int k = abs(count1 - count2);ListNode* LongA = a;ListNode* shortB = b;if(count2 > count1){LongA = b;shortB = a;}while(k--){LongA = LongA->next;}while(shortB && LongA){LongA = LongA->next;shortB = shortB->next;if (shortB == LongA)return shortB;}}环形链表
环形链表 一

. - 力扣(LeetCode)
如果只用一个指针遍历链表,会在环中死循环。在这到题中我们还是使用快慢指针的解法:定义fast和slow两个指针,fast每次走两步,slow每次走一步。如果没有环,fast会先走到尾节点。如果有环,fast会比slow先到环中,到slow走到环中时便成了追击相遇问题,fast比slow快,总会追到slow,如果fast == slow,就说明链表中有环。
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {ListNode* slow = head;ListNode* fast = head; while(fast && fast->next){fast = fast->next->next;slow = slow->next;if (fast == slow){return true;}}return false;
}延申讨论
当fast一次走三步,slow一次走一步的时候还能相遇吗?会不会错过?
设非环部分的长度为L,环的长度为C,fast距slow为N。
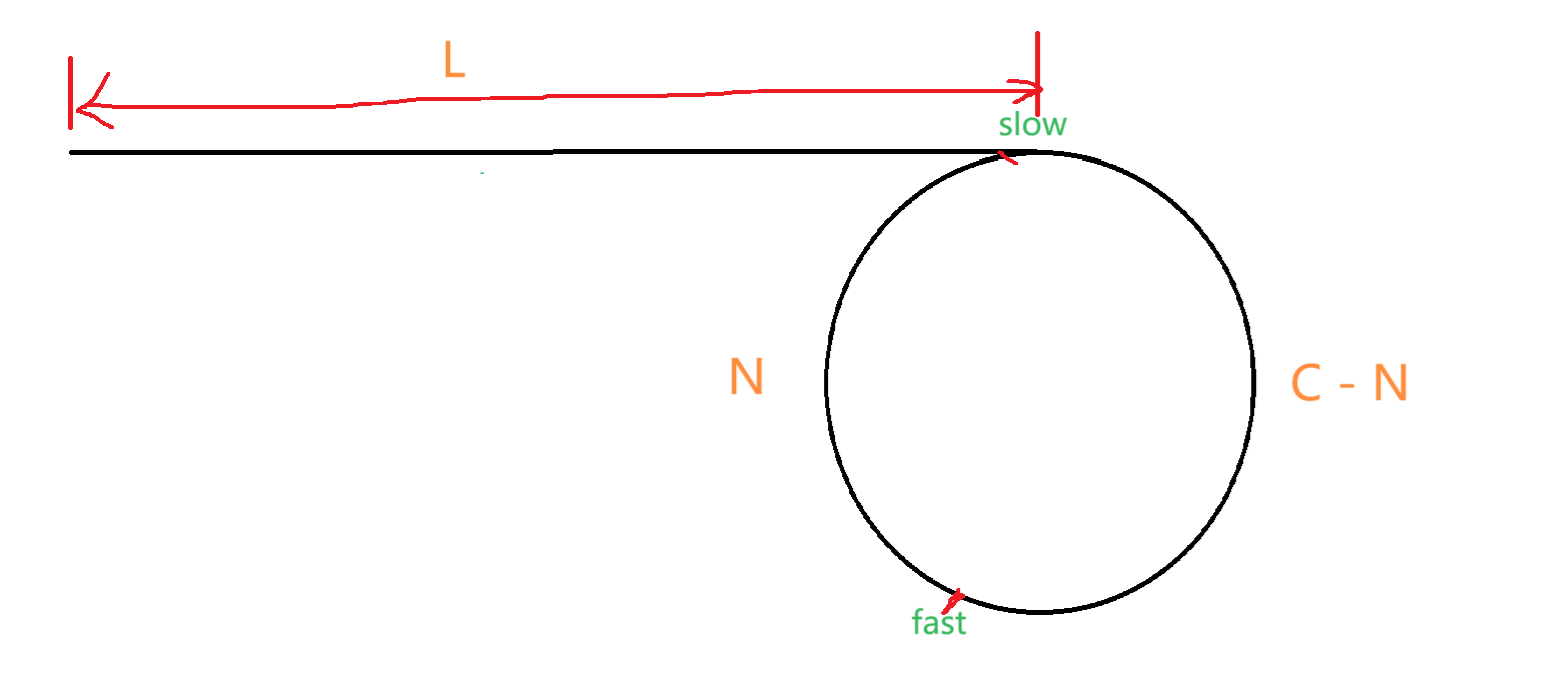
当slow进环后每走一步,相差的距离减少2
依次为 N
N - 2
N - 4
.........
如果N是偶数,那么就可以相遇。如果N为奇数,fast与slow的距离变为C - 1,进入下一次循环,若C - 1为偶数,fast 与slow之间的距离一次依次减少2,最后为0,相遇。若C - 1是奇数,那么fast与slow的距离依次减少2,最后fast与slow又会错过,距离又变为C - 1,依次重复,永远遇不到。
这样算出来,将永远遇不到,但是这样要满足一个条件,N是奇数,C - 1为奇数。我们还有一个条件没有用到fast移动的距离是slow的3倍,以此可得:


2 * L必为偶数,那么若C - 1为奇数,C就为偶数,N必为偶数,所以不相遇的条件不存在。
fast与slow必会相遇。
这种数理上的题就是为了筛选出的,为了考核。虽然可能没什么应用的意义,但是考查了数理能力,在面试的时候解出来会让面试官眼前一亮。
环形链表 二

. - 力扣(LeetCode)
定义fast和slow两个指针,slow每次走一步,fast每次走两步。设环长为C,非环部分长为L,当slow与fast相遇的时候,slow又走的距离为N。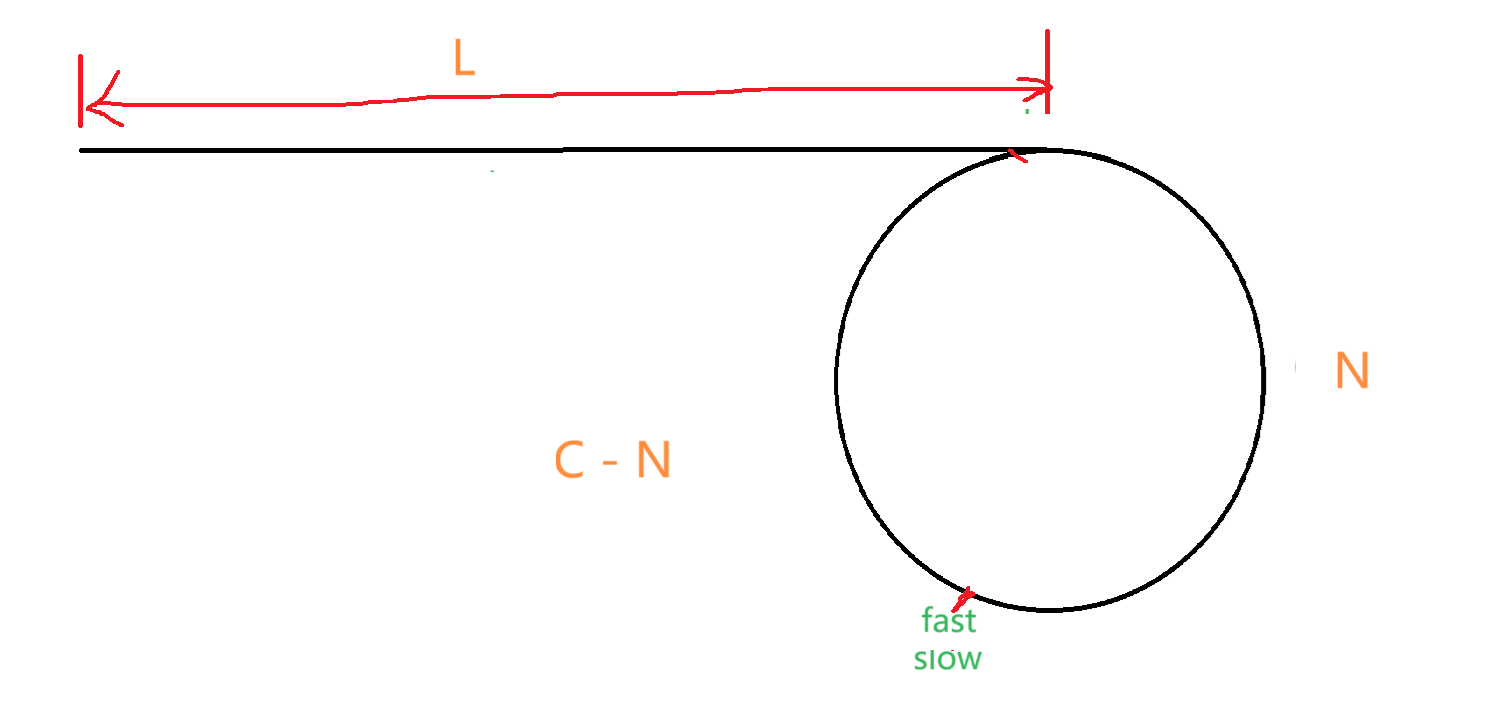
就和高中的物理题一样,我们要找等式关系。设fast所走的总路程为F,slow的为S,当slow与fast相遇时:
F = L + N + x * C (假设fast在环中已经走了x圈)
S = L + N
F是S的2倍。L + N + x * C = 2( L + N )
化简为: L = x *C - N = ( x - 1 ) * C + C - N
重新定义一个节点cmp从头开始一步一步走,设slow和fast相交的点为meet,同时开始一步一步走。所以cmp走了( x - 1 ) * C 过后还剩 C - N;meet走了(x - 1)* C回到原点到原点。这时,cmp和meet都相距环的起点C - N。当它们相遇时,这个节点即为所求。
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) {ListNode* slow = head;ListNode* fast = head; while(fast && fast->next){fast = fast->next->next;slow = slow->next;if (fast == slow){ListNode * new = head;while(slow != new){slow = slow->next;new = new->next;}return new;}}return NULL;
}