##O(n^2)算法时间复杂度的排序算法

目录

##O(n^2)算法时间复杂度的排序算法

##选择排序

##原理

##图例

##代码实现示例

##冒泡排序

##原理

##图例

##代码实现示例

##插入排序

##原理

##图例

##代码实现示例

##总结 

---

##选择排序

##原理

在一个无序的数组或者列表中，从第一个元素到最后一个元素中选择一个最小的元素与第一个元素进行交换，即第一个元素位置就变成了有序区域，而对于无序区域重复以上过程，一个完整的选择排序就实现完成了。

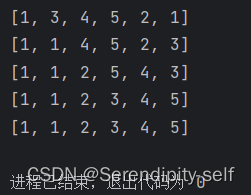
##图例

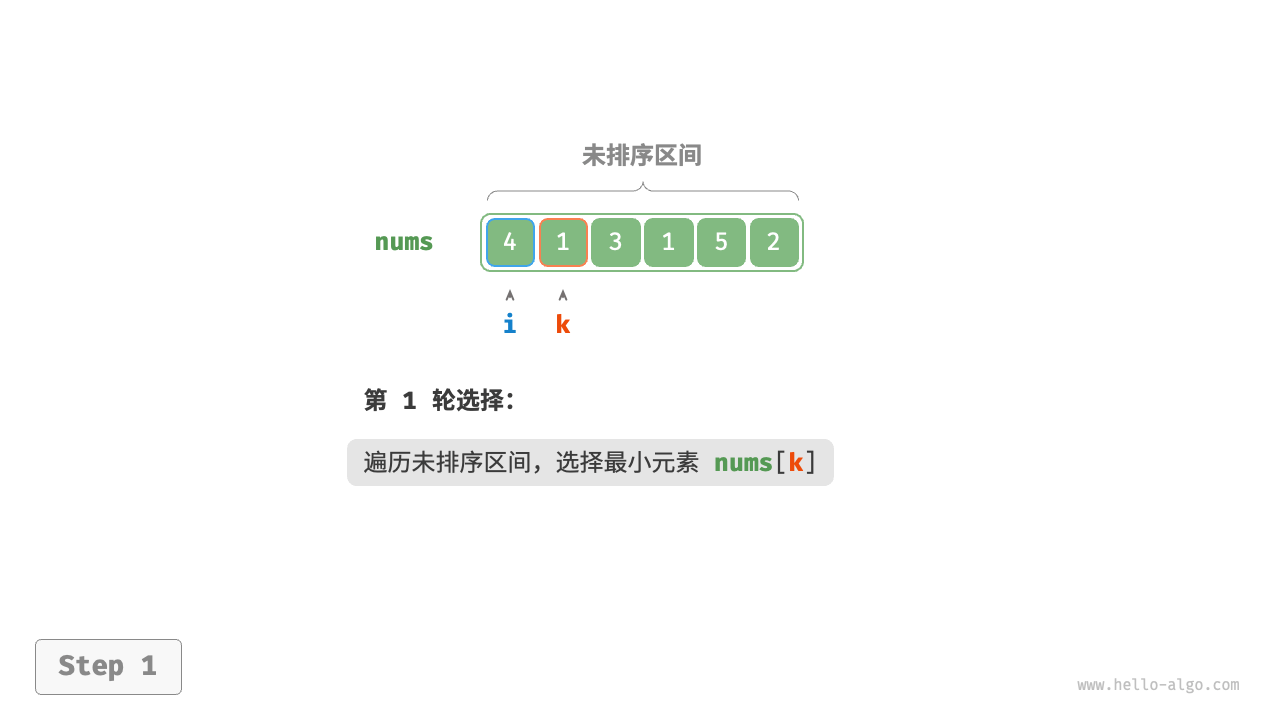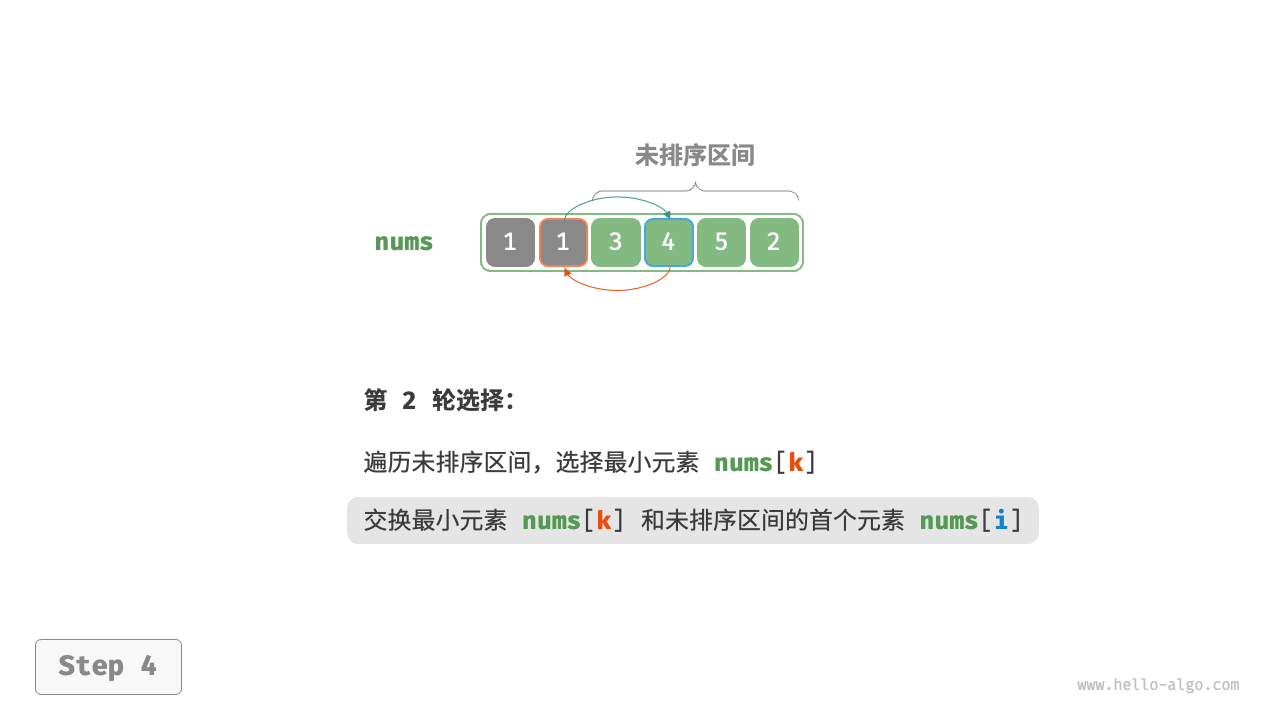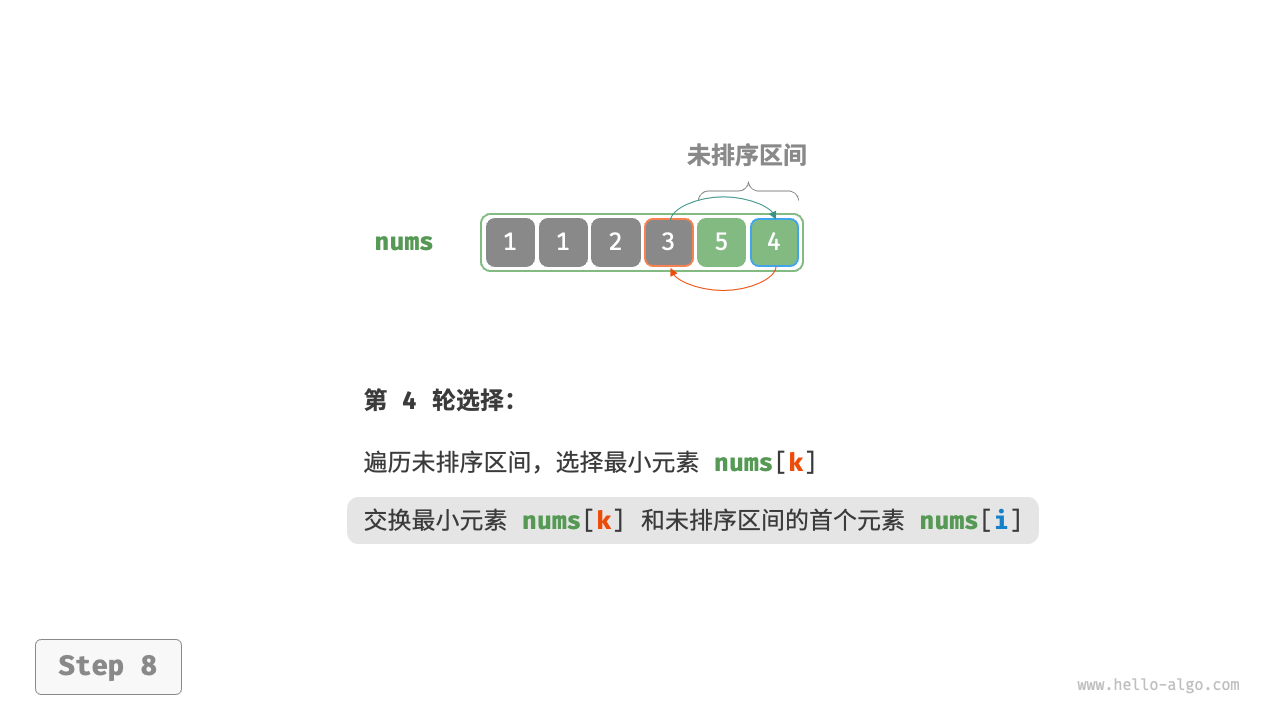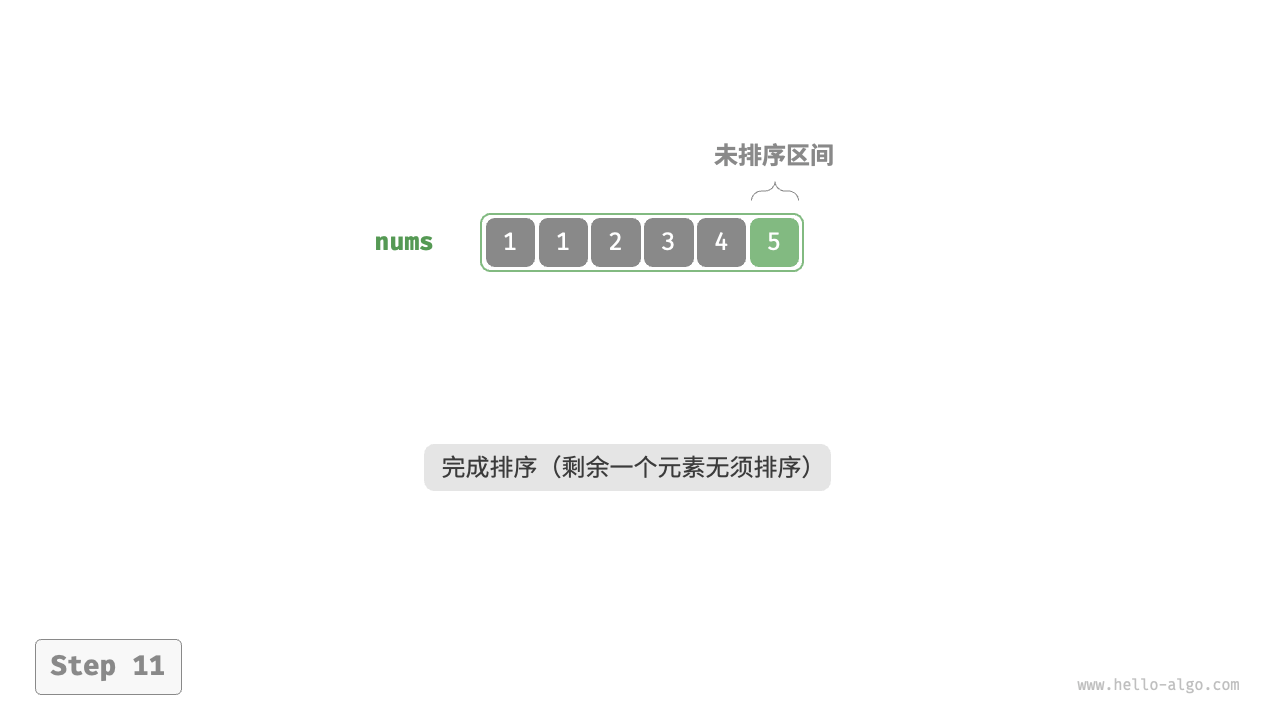
##代码实现示例

#python代码示例
def SelectionSort(ls) :n = len(ls)#这里为什么是n-1呢这里说明一下#我们要进行n-1轮的选择for i in range(n-1) :min = i #设置当前位置为最小值for j in range(i+1,n) : #从当前位置开始到最后一个位置进行选择if ls[j] < ls[min] :min = jls[min],ls[i] = ls[i],ls[min]print(ls) #查看每一轮的选择结果，便于理解
ls = [2,3,4,5,1,1]
SelectionSort(ls)

//c++代码示例
void selection_sort(vector<int> &a)
{int n = a.size() ;for (int i = 0 ; i < len - 1 ; i++){int min = i ;for (int j = i + 1 ; j < len ; j++){if (a[j] < a[min]){min = j ; //记录最小元素的索引}}if (min != i) //交换操作，也可以利用swap函数 swap(a[i],a[min]){int temp = a[min] ;a[min] = a[i] ;a[i] = temp ;}}
}

##冒泡排序

##原理

通过连续地比较与交换相邻元素实现排序。这个过程就像气泡从底部升到顶部一样，因此得名冒泡排序。(不仅仅可以实现递增顺序，同样也可以实现递减顺序)，每一次循环都会形成一个有序区域和无序区域。

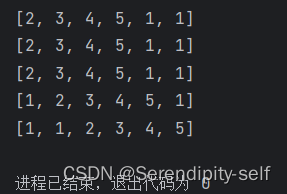
##图例

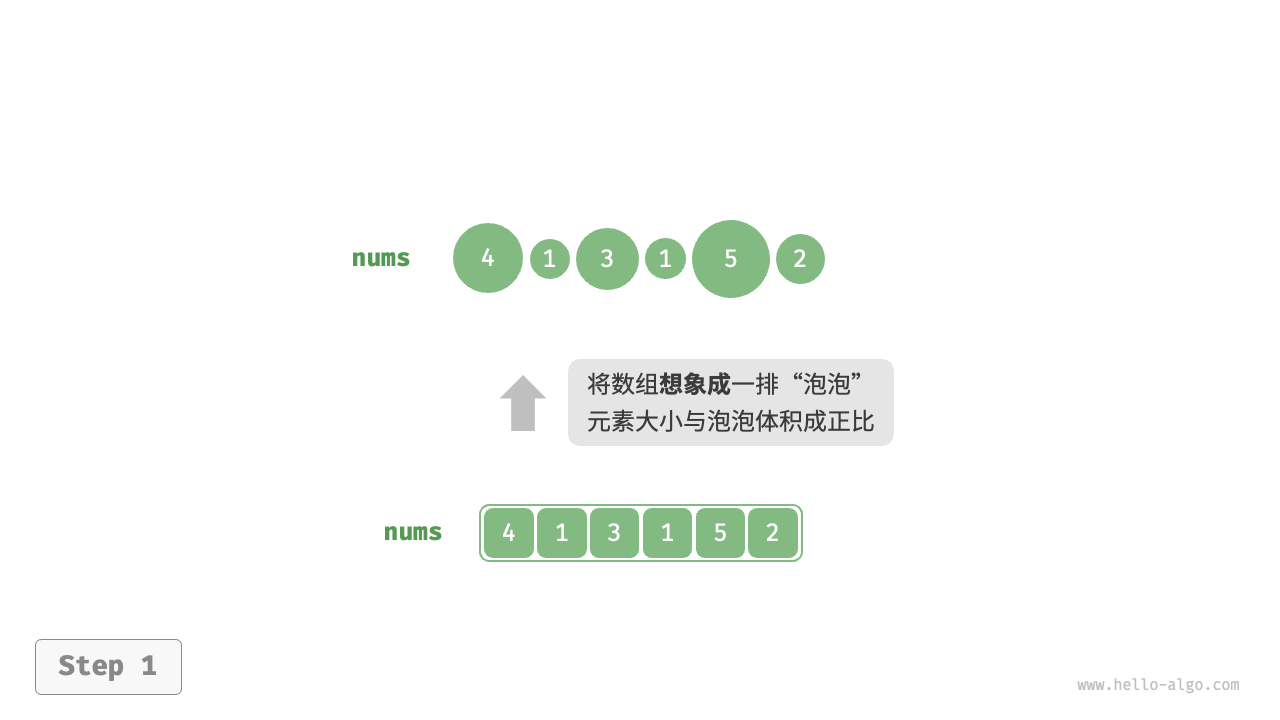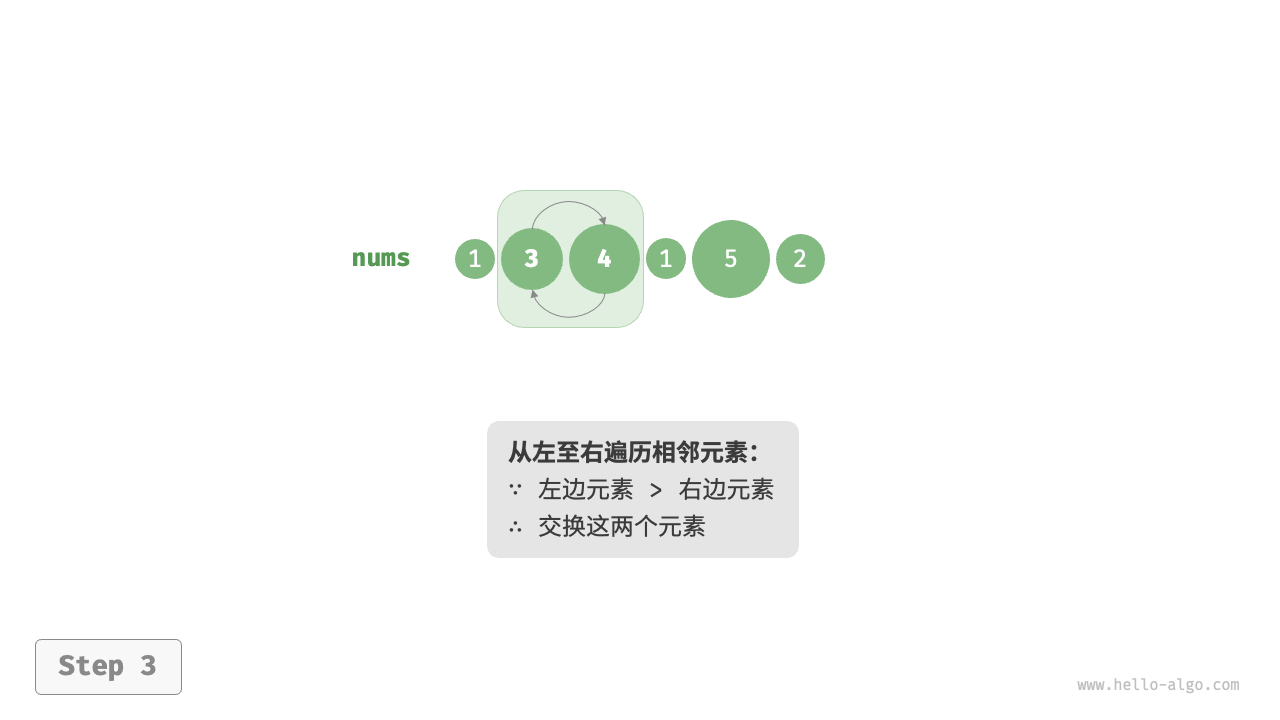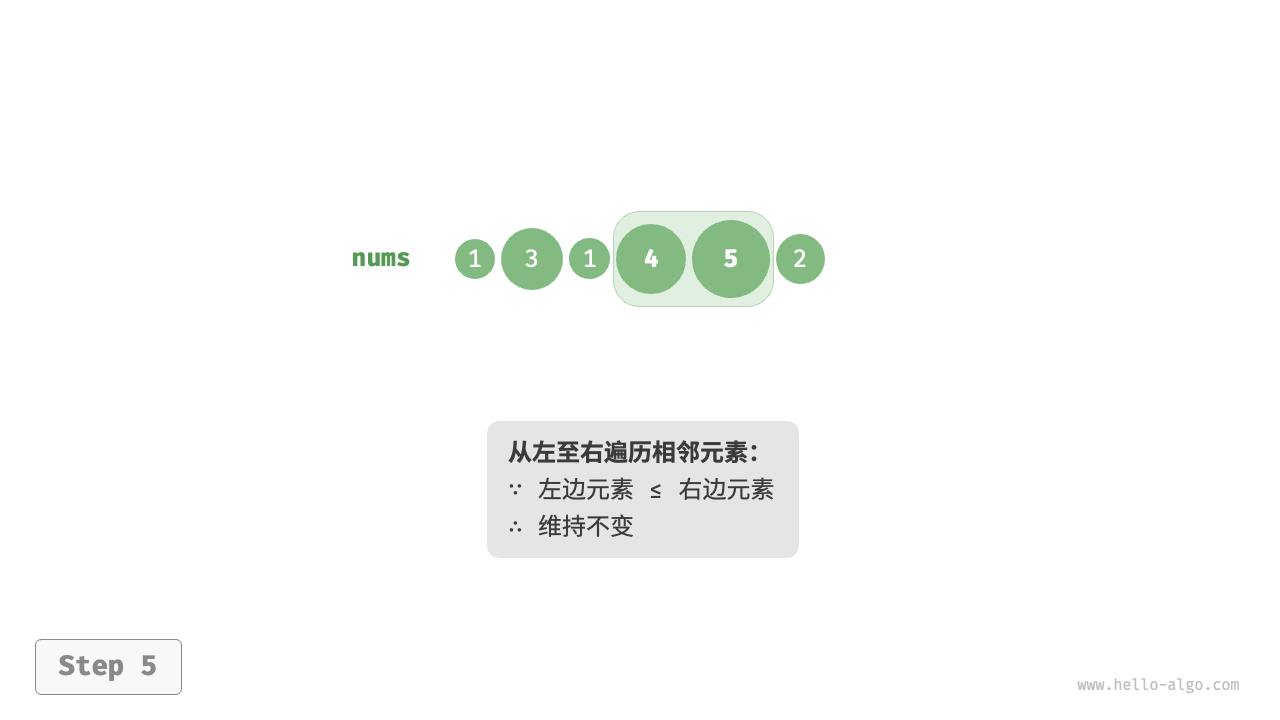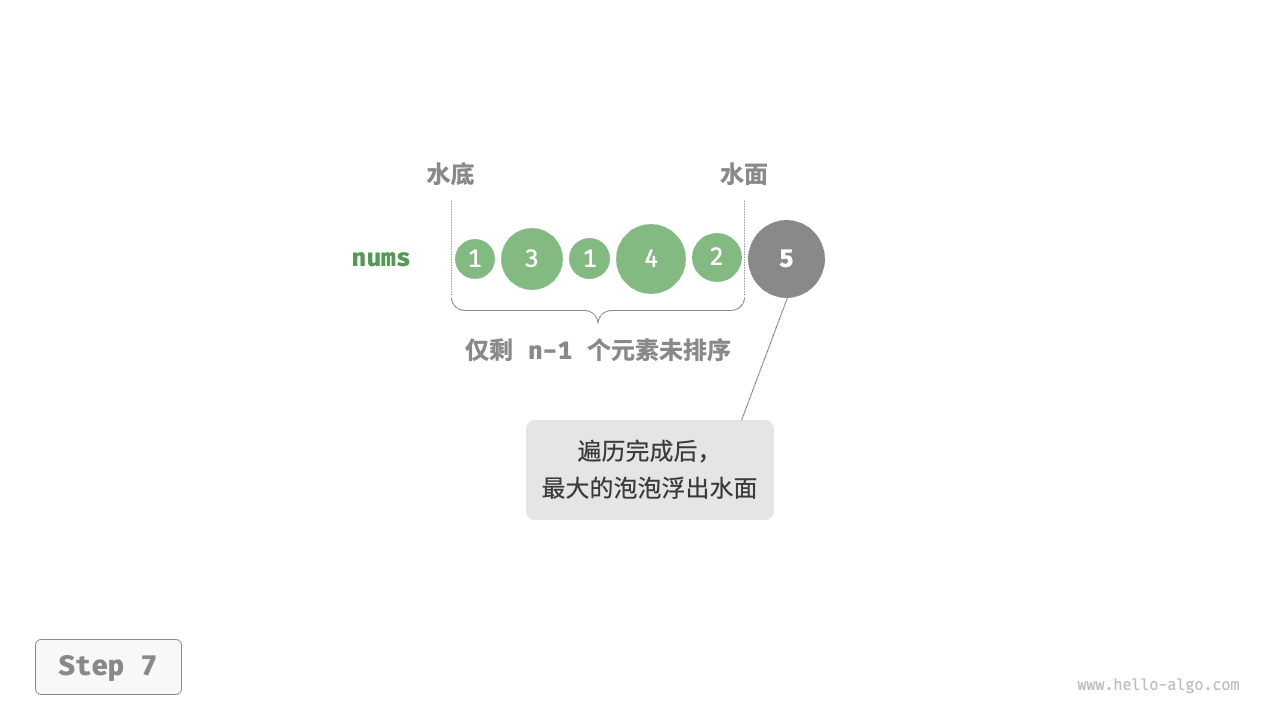
##代码实现示例

//c++代码示例
void bubble_sort(vector<int> &nums)
{int n = nums.size() ;//外循环未排序的区域为[0,i]for (int i = n - 1 ; i > 0 ; i--){//内循环，将未排序的区域[0,i]中的最大元素交换至区间的最右端for (int j = 0 ; j < i ; j++){if (nums[j+1] < nums[j]){//可以使用std::swap()函数，进行交换int temp = nums[j+1] ;nums[j+1] = nums[j] ;nums[j] = temp ;}}}
}

def BubbleSort(ls):n = len(ls)for i in range(n-1,0,-1) : #这里说明以下为什么不是range(n-1,-1,-1),因为自己不需要和自己比较for j in range(i) :if ls[j] > ls[j+1] :ls[j],ls[j+1] = ls[j+1],ls[j]print(ls) #查看交换结果，便于理解整个过程

##插入排序

##原理

我们在未排序区间选择一个基准元素，将该元素与其左侧已排序区间的元素逐一比较大小，并将该元素插入到正确的位置。

我们将基准元素作为一个有序区，然后遍历无序区将无序区的元素插入到有序区域的适合位置。

##图例

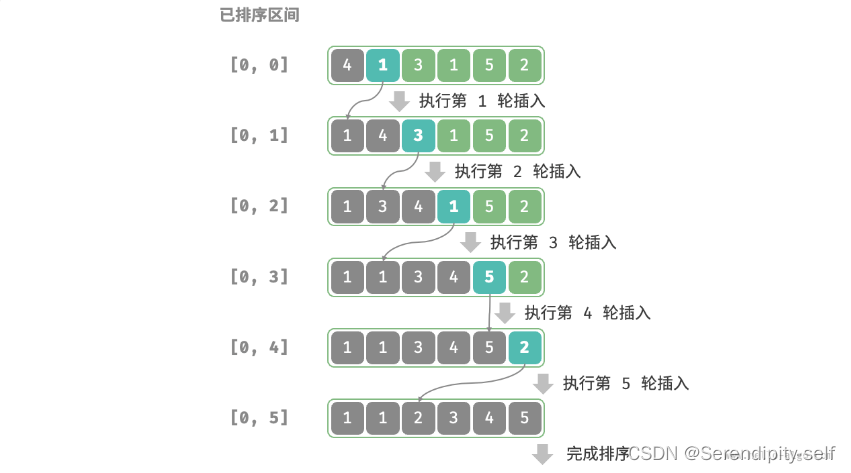
##代码实现示例

1

def InsertSort(ls) :n = len(ls)for i in range(1,n) : #选取第一个元素为基准值,循环下标从1开始x = ls[i] #记录未排序区间的待插入元素j = i - 1 #遍历有序区域，找到待插入的位置while j >= 0 : if x <= ls[j] : #若待插入元素小于当前有序区的元素，有序区元素后移一位ls[j+1] = ls[j]else :breakj -= 1ls[j+1] = x #将元素插入到指定位置print(ls) #查看每一步的插入

3

void bubble_sort(vector<int> &nums)
{int n = nums.size() ;for (int i = 1 ; i < n ; i++){base = nums[i] ;j = i - 1 ;while (j >= 0 && base < nums[j]){nums[j+1] = nums[j] ; 向右移动一位j-- ;}nums[j+1] = base ; }
}

##总结 

• 冒泡排序基于元素交换实现，需要借助一个临时变量，共涉及 3 个单元操作；插入排序基于元素赋值实现，仅需 1 个单元操作。因此，冒泡排序的计算开销通常比插入排序更高。
• 选择排序在任何情况下的时间复杂度都为 𝑂(n^2) 。如果给定一组部分有序的数据，插入排序通常比选择排序效率更高。
• 选择排序不稳定，无法应用于多级排序。