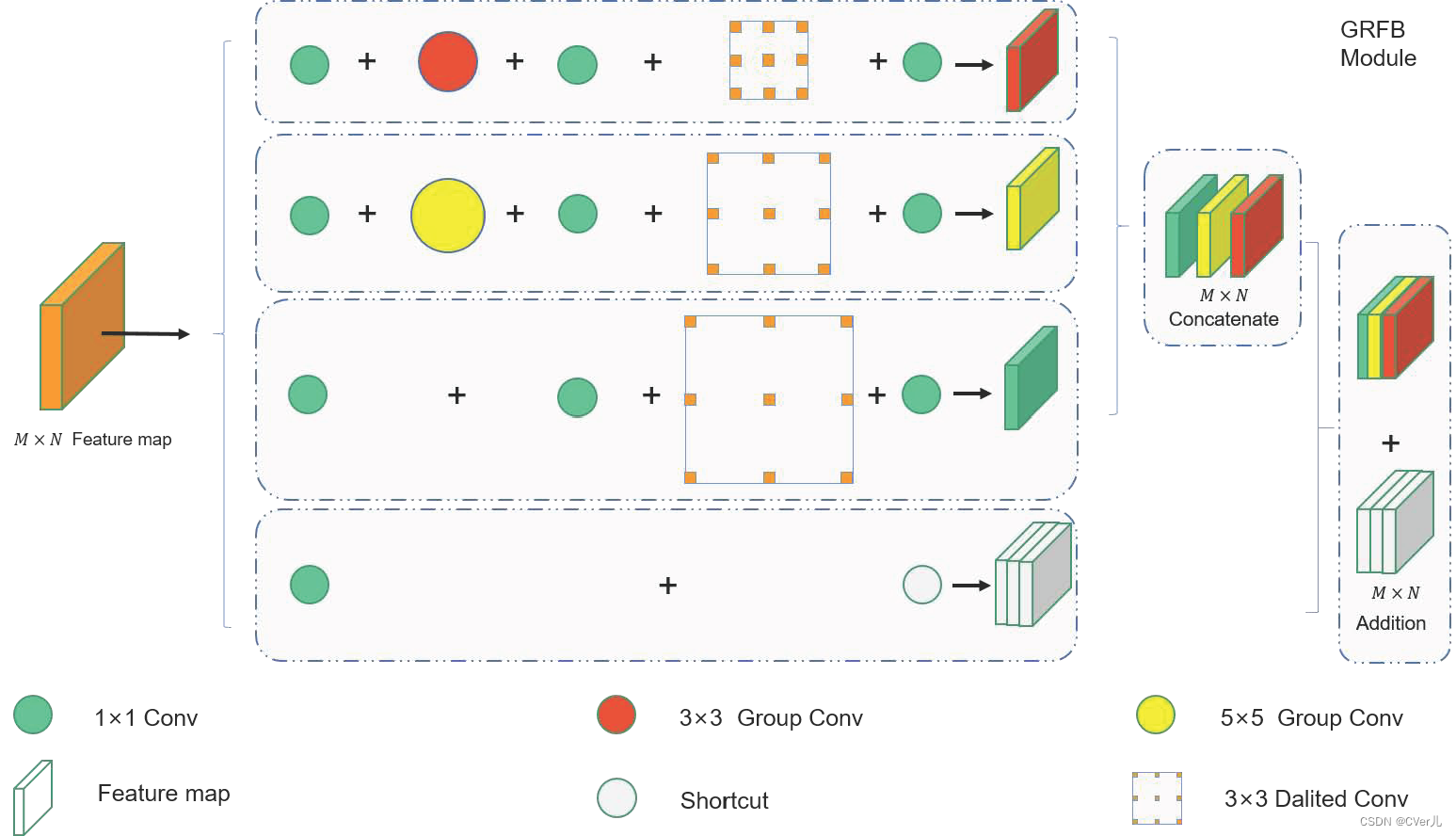
在一个无序数组里有99个不重复的正整数,范围是1~100,唯独缺少1个1~100中的整数。如何找出这个缺失的整数?
一个很简单也很高效的方法,先算出1~100之和,然后依次减去数组里的元素,最后得到的差值,就是那个缺失的整数。
假设数组长度是n,那么该解法的时间复杂度是O (n),空间复杂度是O (1)。
import random
#数组
def find_1(n):ll=[]#随机生成1-n的一个数作为缺失数rd= random.randint(1,n+1)# print(rd)#循环数据for i in range(1,n+1):if i!=rd:ll.append(i)print(ll)return ll#查找缺失的整数
def find_number(n):ll=find_1(n)#累计和sum1=sum(ll)#累计1..n和sum2=((1+n)*n)//2print(sum1,sum2)return sum2-sum1if __name__ == '__main__':# print(find_number(10))print(find_number(100)) 

扩展题1:
一个无序数组里有若干个正整数,范围是1~100,其中99个整数都出现了偶数次,只有1个整数出现了奇数次,如何找到这个出现奇数次的整数?
遍历整个数组,依次做异或运算。由于异或运算在进行运算时,相同为0,不同为1,
因此所有出现偶次的整数都会相互抵消成为0,只有唯一出现奇数的整数会被留下。

def find2(ll):lost=0for i in range(len(ll)):#异或运算lost=lost^ll[i]return lostif __name__ == '__main__':ll=[3,1,3,2,2,8,1]print(find2(ll))如果数组长度为n,该解法的时间复杂度是O(n),空间复杂度为O(1)。
扩展题2:
假设一个无序数组里有若干个正整数, 范围是1~ 100, 其中有98个整数出现了偶数次, 只有2个整数出现了奇数次, 如何找到这2个出现奇数次的整数?
使用分治算法,设这两个整数为A,B。
1、先将数组内元素异或得到A,B的异或值。
2、将该值对应的二进制位从右至左找到第一个为1的值sep,表示A,B对应的二进制表示在此处的位置相异,设A为1,B为0。
3、利用此区别,将数组中的其他元素和sep相与,为1和A划为一组,为0和B划为一组。
4、利用扩展1求解。

def find3(ll):# 用于存储两个出现奇数次的整数result=[0,0]# 第一次整体异或lost = 0for i in range(len(ll)):# 异或运算lost = lost ^ ll[i]# 如果异或结果为0,说明输入数组不符合题目if lost==0:raise ValueError# 确定两个整数的不同位,以此来做分组sep=1while lost & sep==0:sep<<=1# 第二次分组异或for i in range(len(ll)):if ll[i] & sep==0:result[0]^=ll[i]else:result[1]^=ll[i]return resultif __name__ == '__main__':ll=[3,1,3,2,2,8,1,4]print(find3(ll))
如果数组长度是n,该解法的时间复杂度是O(n)。把数组分成两部分,并不需要借助额外的存储空间,完全可以在按二进制位分组的同时来做异或运算,所以空间复杂度仍然是O(1) 。