二叉树基础oj练习【11道题】

二叉树基础oj练习

1.单值二叉树

题目：

单值二叉树

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。

示例 1：

img

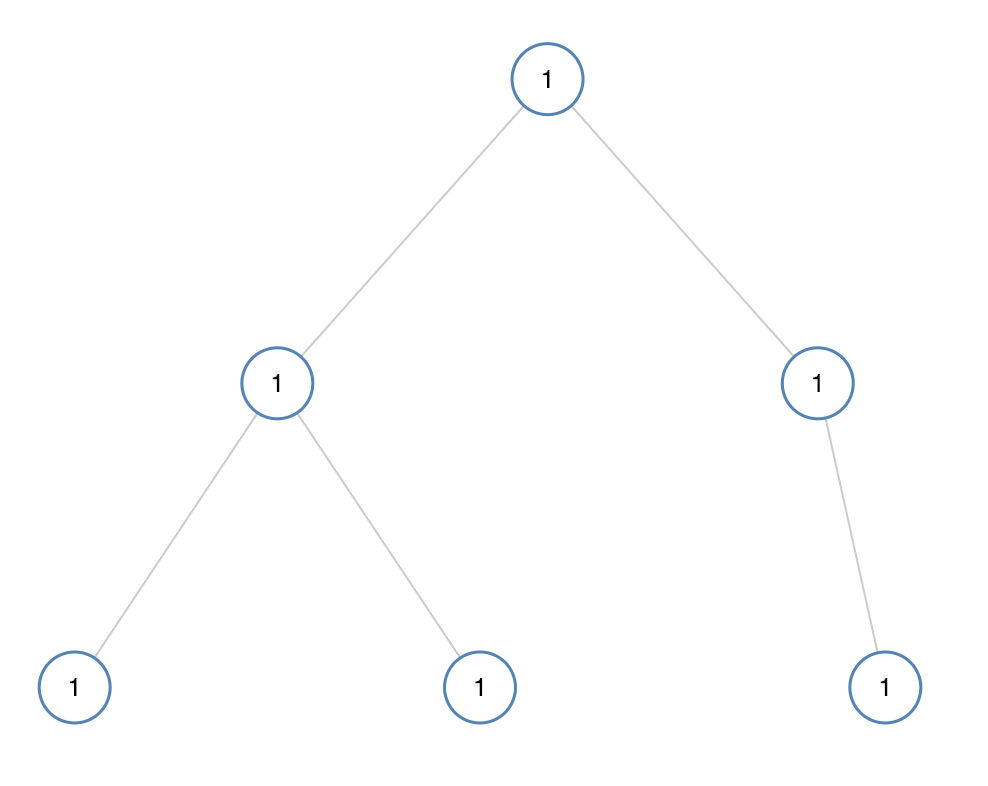
输入：[1,1,1,1,1,null,1]
输出：true

示例 2：

img

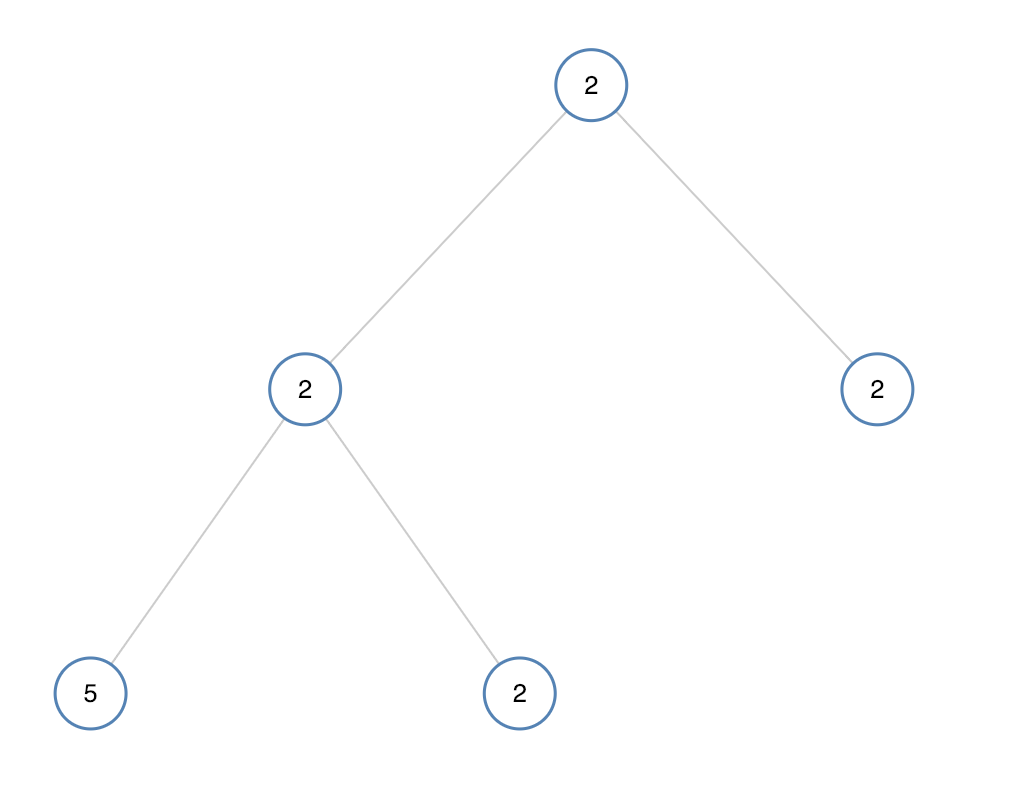
输入：[2,2,2,5,2]
输出：false

提示：

  1. 给定树的节点数范围是 [1, 100]。
  2. 每个节点的值都是整数，范围为 [0, 99] 。

思路：

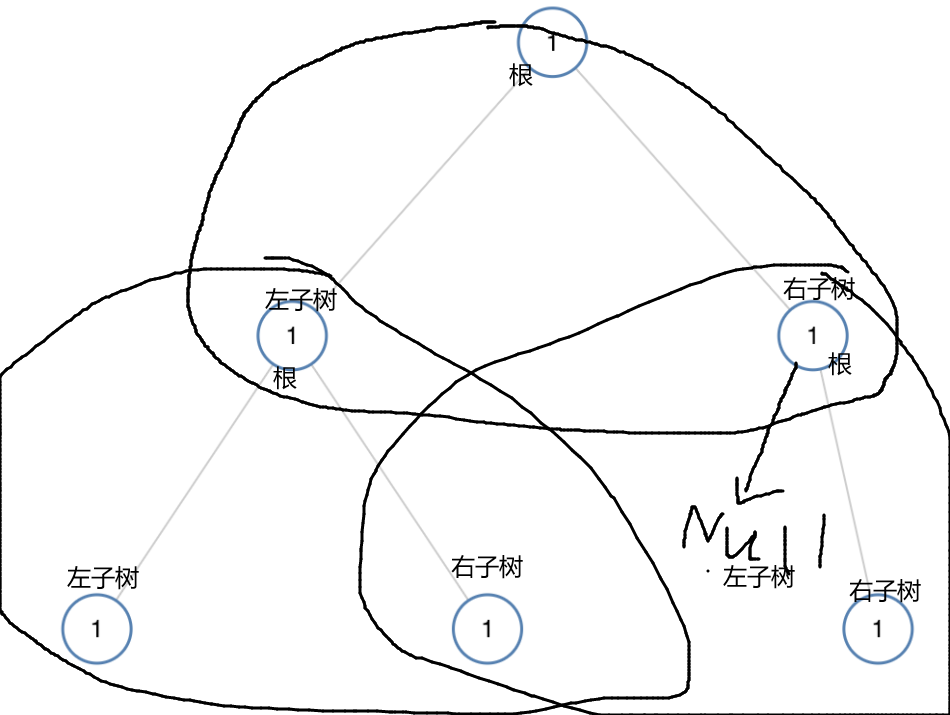
image-20240512232747144

如图所示，我们采取前序遍历二叉树，让每个根都去和他的左子树和右子树的值去比较。

一旦有不同就返回false，都相同就一直遍历，直至找到叶子结点，也就是root是NULL的时候，返回true。

代码：

struct TreeNode 
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isUnivalTree(struct TreeNode* root)
{// 如果一开始就是NULL 那就相当于全部节点都是NULL// 如果一直判断都找不到不一样的值，就说明全都是一样的，// 如果全部前序遍历的递归函数全部都返回true，那就是单值二叉树if (root == NULL)return true;// 让当前根节点，去和左右孩子对比if (root->left && root->left->val != root->val)return false; // 不一样就返回falseif (root->right && root->right->val != root->val)return false;// 这里其实就是前序遍历二叉树return isUnivalTree(root->left) && isUnivalTree(root->right);
}

2.二叉树的最大深度

题目：

二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

img

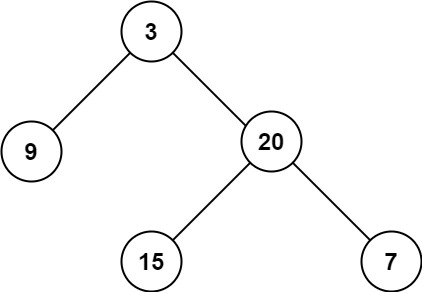
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

  • 树中节点的数量在 [0, 104] 区间内。
  • -100 <= Node.val <= 100

思路：

求出左子树的深度和右子树的深度，判断谁大， 大的就 + 1

代码：

struct TreeNode
{int val;struct TreeNode* left;struct TreeNode* right;};int maxDepth(struct TreeNode* root)
{if (root == NULL)return 0;// 计算左子树的深度 和 右子树的深度int leftdepth = maxDepth(root->left);int rightdepth = maxDepth(root->right);// 判断谁大，大的深度+1 就是最大深度return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
}

3.翻转二叉树

题目：

翻转二叉树

给定一棵二叉树的根节点 root，请左右翻转这棵二叉树，并返回其根节点。

示例 1：

img

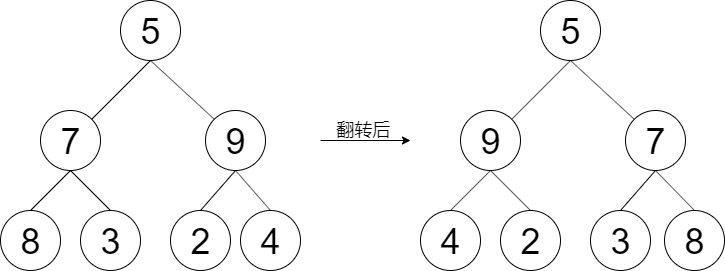
输入：root = [5,7,9,8,3,2,4]
输出：[5,9,7,4,2,3,8]

提示：

  • 树中节点数目范围在 [0, 100] 内
  • -100 <= Node.val <= 100

思路：

  • 如果root不为空，那就交换其左子树和右子树

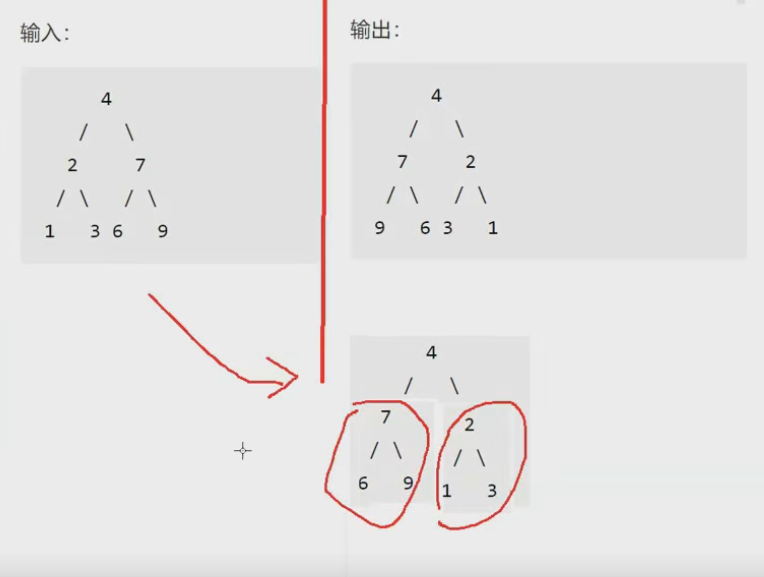
image-20240513120414247

然后让每个左子树和右子树都要调转顺序就行了

代码：

思路1：
struct TreeNode 
{int val;struct TreeNode* left;struct TreeNode* right;
};typedef struct TreeNode TreeNode;// 第一种思路 (前序)
TreeNode* mirrorTree(TreeNode* root)
{if (root == NULL)return  NULL;// 让根原本指向的左子树和右子树 调转  // 让指向左子树的指针，指向右子树，指向右子树的指针指向左子树TreeNode* tmp = root->left;root->left = root->right;root->right = tmp;// 每个左子树和右子树都要翻转mirrorTree(root->left);mirrorTree(root->right);ret
思路2：
// 第二种思路 (中序和后序结合)
TreeNode* mirrorTree(TreeNode* root)
{if (root == NULL){return NULL;}else{// 先让左子树翻转，翻转完会返回左子树的根节点，让指向右子树的指针指向这个节点// 右子树同理// 这样就实现了根节点的左右子树翻转TreeNode* right = root->right;root->right = mirrorTree(root->left);root->left = mirrorTree(right);return root;}}

4.二叉树的前序遍历

题目：

二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

img

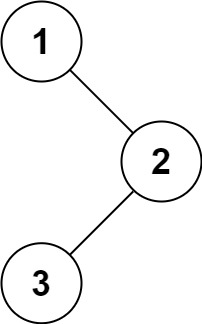
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

img

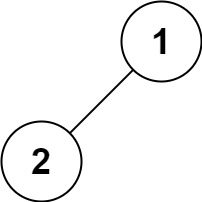
输入：root = [1,2]
输出：[1,2]

示例 5：

img

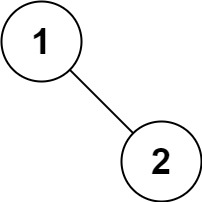
输入：root = [1,null,2]
输出：[1,2]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

思路：

  1. 其实就是要让二叉树前序遍历
  2. 但是题目需要我们将遍历到的节点的值放进数组里面，而我们又不知道二叉树有多少个节点，这样就不知道数组要开辟多少空间，
  3. 因此我们需要先编写一个获取二叉树节点个数的函数
  4. 然后就让前序遍历二叉树，把遍历到的值放进数组中就行了
  5. 但是需要注意的是，传数组的下标i进去的时候，需要传址调用（因为我们采用递归来实现前序遍历）

代码：

struct TreeNode 
{int val;struct TreeNode* left;struct TreeNode* right;};/** Note: The returned array must be malloced, assume caller calls free().*/typedef struct TreeNode TreeNode;// 获取二叉树的节点个数
int TreeSize(TreeNode* root)
{if (root == NULL){return 0;}return 1 + TreeSize(root->left) + TreeSize(root->right);
}// 前序遍历  （递归实现）
void _preorderTraversal(TreeNode* root, int* retArr, int* pi)
{if (root == NULL)return;retArr[(*pi)] = root->val; // i 的值我们通过解引用去拿到(*pi)++;_preorderTraversal(root->left, retArr, pi);_preorderTraversal(root->right, retArr, pi);
}int* preorderTraversal(struct TreeNode* root, int* returnSize)
{// 创建一个数组 空间个数是二叉树的节点数int* retArr = (int*)malloc(sizeof(int) * TreeSize(root));// 前序遍历 (要把二叉树节点的值 放进retArr数组中)int i = 0;_preorderTraversal(root, retArr, &i);// 这里是一定要传 i的地址的，不然每次递归的时候，都会开辟新的函数栈帧，i的值无法被改变。 传值调用// 传地址进去就是 传址调用*returnSize = TreeSize(root);return retArr;
}

要注意递归展开的过程，理解了就能知道为什么要传址调用了。

5.二叉树的中序遍历

题目：

二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

img

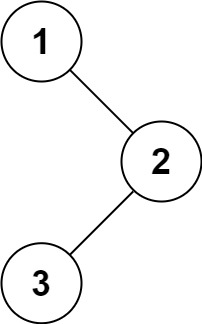
输入：root = [1,null,2,3]
输出：[1,3,2]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

思路：

中序遍历 - 左子树 ——根——右子树

除了要在递归的时候注意顺序，其他思路和前序是一样的。

代码：

typedef struct TreeNode TreeNode;// 获取二叉树节点个数
int TreeSize(TreeNode* root)
{if (root == NULL)return 0;// 二叉树节点个数 = 1 + 左子树节点个数 + 右子树节点个数return 1 + TreeSize(root->left) + TreeSize(root->right);
}// 中序遍历
void _inorderTraversal(TreeNode* root, int* retArr, int* pi)
{if (root == NULL)return;// 这里我们要中序遍历，【左子树 根 柚子树】_inorderTraversal(root->left, retArr, pi);retArr[(*pi)] = root->val;(*pi)++;_inorderTraversal(root->right, retArr, pi);
}int* inorderTraversal(struct TreeNode* root, int* returnSize)
{// 要将遍历到的节点放进数组中// 我们不知道二叉树节点多少，也就不知道数组要开辟多少空间。因此需要自己写一个获取二叉树节点个数的函数int size = TreeSize(root);int* retArr = (int*)malloc(sizeof(int) * size);//中序遍历）（递归实现）int i = 0;_inorderTraversal(root, retArr, &i);*returnSize = size;return retArr;
}

6.二叉树的后序遍历

题目：

二叉树的后序遍历

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

示例 1：

img

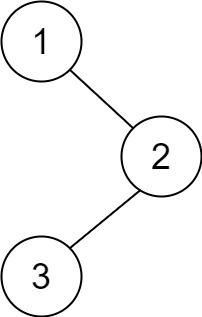
输入：root = [1,null,2,3]
输出：[3,2,1]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

提示：

  • 树中节点的数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

思路：

后序遍历 - 左子树——右子树——根

注意递归时的调用顺序，其他思路和前序中序差不多。

代码：

struct TreeNode 
{int val;struct TreeNode* left;struct TreeNode* right;};/** Note: The returned array must be malloced, assume caller calls free().*/typedef struct TreeNode TreeNode;// 获取二叉树的节点个数
int TreeSize(TreeNode* root)
{if (root == NULL){return 0;}return 1 + TreeSize(root->left) + TreeSize(root->right);
}// 后序遍历
void _postorderTraversal(TreeNode* root, int* retArr, int* pi)
{if (root == NULL)return;// 后序遍历 【左子树 右子树 根】_postorderTraversal(root->left, retArr, pi);_postorderTraversal(root->right, retArr, pi);retArr[(*pi)] = root->val;(*pi)++;
}int* postorderTraversal(struct TreeNode* root, int* returnSize)
{// 要将遍历到的节点放进数组中// 我们不知道二叉树节点多少，也就不知道数组要开辟多少空间。因此需要自己写一个获取二叉树节点个数的函数int size = TreeSize(root);int* retArr = (int*)malloc(sizeof(int) * size);// 后序遍历（递归实现）int i = 0;_postorderTraversal(root, retArr, &i);*returnSize = size;return retArr;
}

7.相同的树

题目：

相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

img

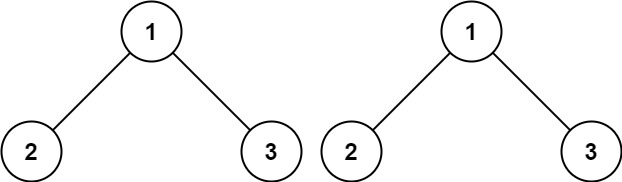
输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

img

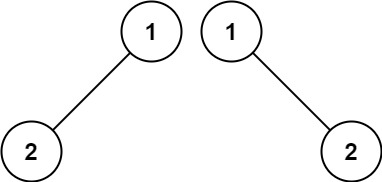
输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

img

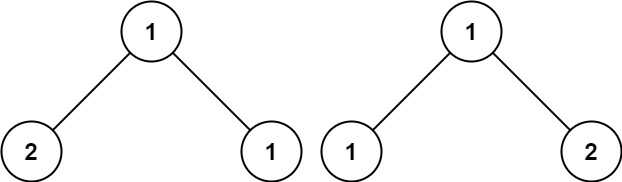
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

  • 两棵树上的节点数目都在范围 [0, 100] 内
  • -104 <= Node.val <= 104

思路：

  1. 首先我们要对传进来的两个树，是否是空树进行判断。
  2. 不是空树我们就要去判断他们的结构是否相同，也是为了防止对NULL进行解引用
  3. 结构都相同那就去判断他们的值是否相同，不同就返回false
  4. 然后通过递归去判断两个数的每一个节点是否相同

代码：

struct TreeNode 
{int val;struct TreeNode* left;struct TreeNode* right;
};bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{// 判断传进来的两棵树是否是空树if (p == NULL && q == NULL)return true;// 为了防止对NULL解引用，我们要先对其结构判断是否相同if (p != NULL && q == NULL)return false;if (p == NULL && q != NULL)return false;// 如果结构相同，就要判断其值是否相同if (p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

8.对称二叉树

题目：

对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

img

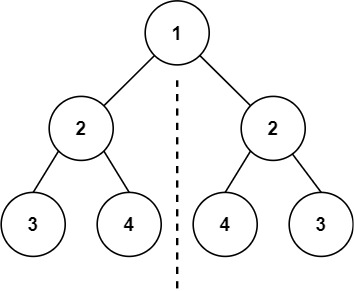
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

img

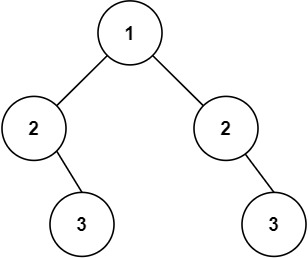
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

  • 树中节点数目在范围 [1, 1000] 内
  • -100 <= Node.val <= 100

**进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

思路：

  1. 首先我们要判断传进来的树是否是空树，空树就是true。
  2. 然后我们要判断根的左子树和右子树结构是否轴对称，结构都不轴对称，false
  3. 结构轴对称了我们就要去判断其值是否轴对称

代码:

struct TreeNode 
{int val;struct TreeNode* left;struct TreeNode* right;
};typedef struct TreeNode TreeNode;bool isMirror(TreeNode* left, TreeNode* right)
{// 判断左右子树的结构if (left == NULL && right == NULL)return true;// 左子树或这样右子树有一个是NULL 就是falseif (right == NULL || left == NULL)return false;// 除了结构要对称，也要判断其值是否轴对称return (left->val == right->val) &&isMirror(left->left, right->right) &&isMirror(left->right, right->left);
}bool isSymmetric(struct TreeNode* root)
{// 判断传进来的树是否为空if (root == NULL)return true;// 判断每个左子树右子树是否轴对称return isMirror(root->left, root->right);
}

9.另一棵树的子树

题目：

另一棵树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

img

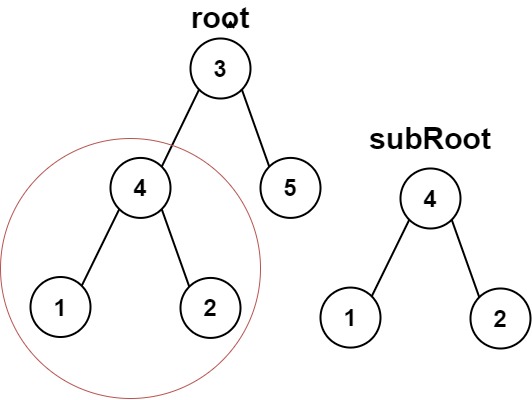
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

示例 2：

img

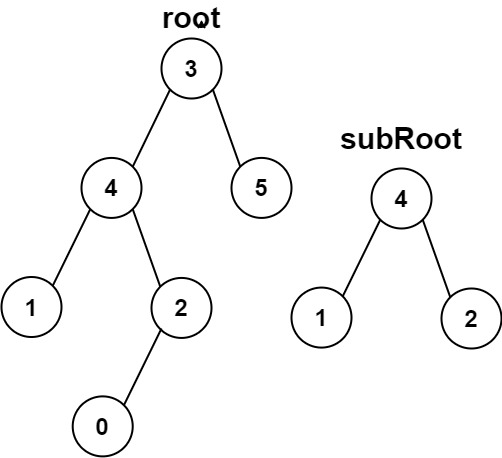
输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
输出：false

提示：

  • root 树上的节点数量范围是 [1, 2000]
  • subRoot 树上的节点数量范围是 [1, 1000]
  • -104 <= root.val <= 104
  • -104 <= subRoot.val <= 104

思路：

让root上的每一课树都去和subRoob这课树去比较是否相同。

在比较树是否相同的时候，要注意结构和值都要比较是否相同。

递归到NULL就要返回

代码：

struct TreeNode 
{int val;struct TreeNode* left;struct TreeNode* right;
};// 判断两棵树是否相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{// 判断传进来的两棵树是否是空树if (p == NULL && q == NULL)return true;// 为了防止对NULL解引用，我们要先对其结构判断是否相同if (p != NULL && q == NULL)return false;if (p == NULL && q != NULL)return false;// 如果结构相同，就要判断其值是否相同if (p->val != q->val)return false;return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot)
{if(root == NULL)return false;// 让root中的每一课树 都去和 subRoot这课树进行比较，如果有相同的，那就是true。// 先让root根结点去和subRoot进行比较if(isSameTree(root, subRoot))return true;// 走到这里，说明根节点不包含subRoob这棵树// 那就继续让root中的左子树和右子树 去比较return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

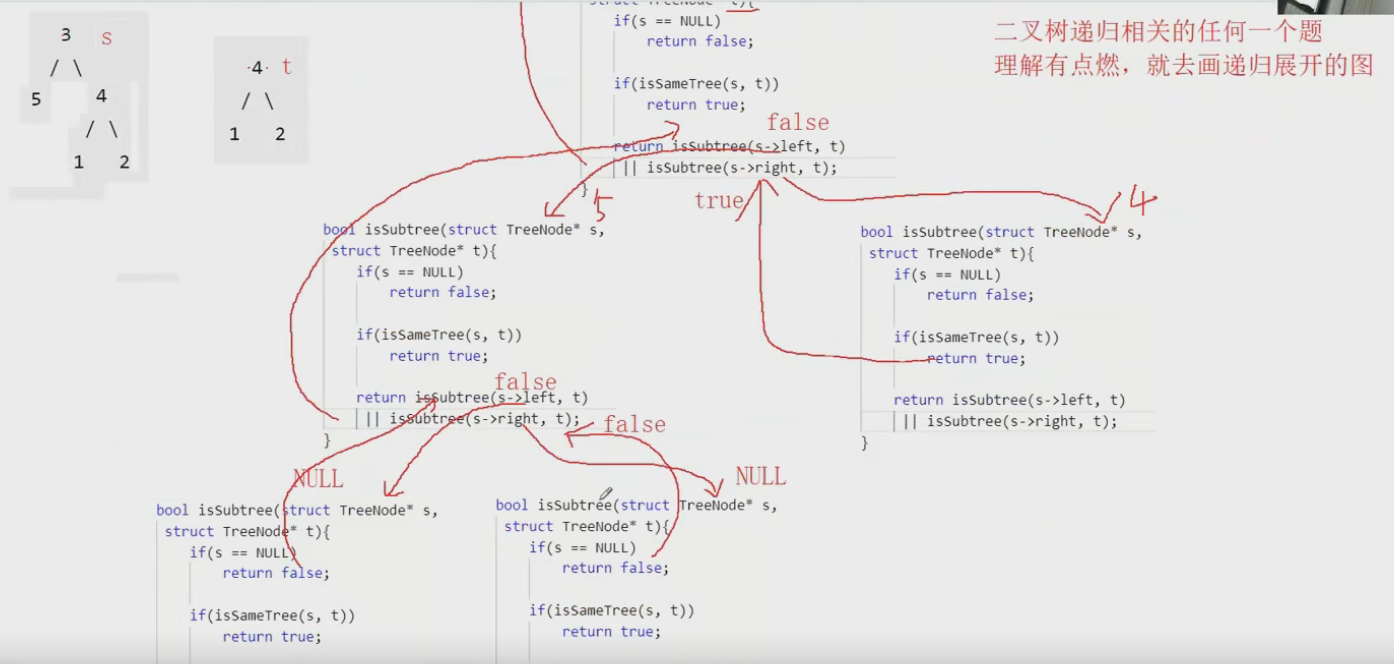
如果理解困难就去画递归展开图

image-20240513202057395

10.平衡二叉树

题目：

平衡二叉树

给定一个二叉树，判断它是否是 平衡二叉树

示例 1：

img

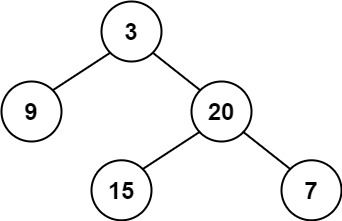
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

img

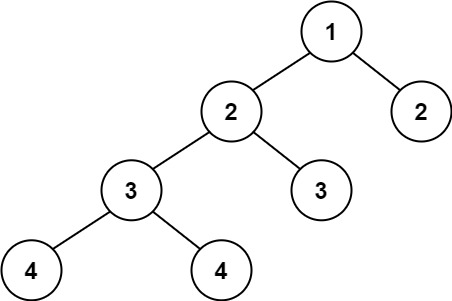
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

  • 树中的节点数在范围 [0, 5000] 内
  • -104 <= Node.val <= 104

思路：

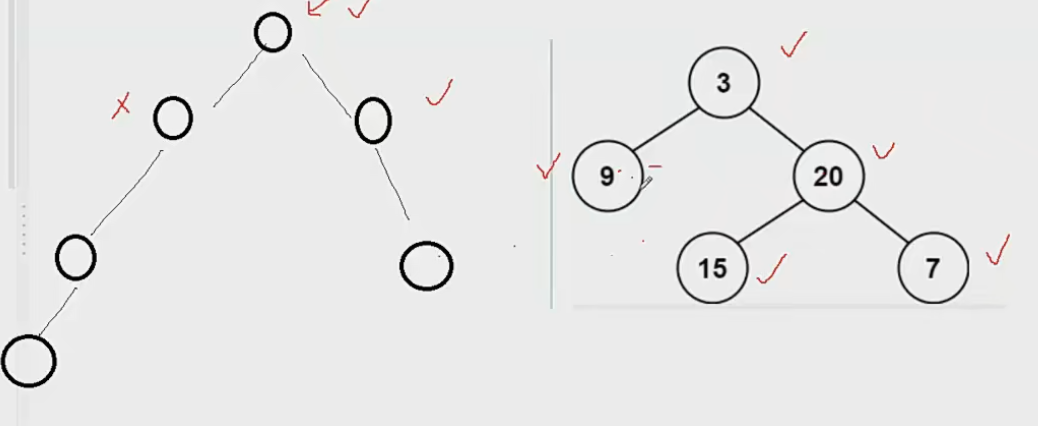
  1. 求出每个根结点的左子树和右子树的高度， 判断其相减的绝对值是否小于等于1
  2. 如果小于等于1 ，那这个根结点代表的子树是平衡二叉树， 但是这样就ok了嘛？
  3. 不是，我们还有继续遍历二叉树，必须是每个子树都是平衡二叉树，整个树才是平衡二叉树。
  4. 因此我们还要接着遍历，判断根结点的左子树代表的子树是否是平衡二叉树，右子树代表的子树是否是平衡二叉树，直至遍历完全部的子树。

image-20240513221453719

代码：

struct TreeNode 
{int val;struct TreeNode* left;struct TreeNode* right;
};// 计算传进来的树 的最大深度
int MaxDepth(struct TreeNode* root) // 时间复杂度为O（N）
{if (root == NULL)return 0;// 左子树和右子树的深度都要计算int leftdepth = MaxDepth(root->left);int rightdepth = MaxDepth(root->right);// 树的深度 = 左子树/右子树 的最大深度 + 1return leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;
}bool isBalanced(struct TreeNode* root) // 时间复杂度为 O(N^2)
{// 如果传进来的根结点，是空，那说明这个根结点代表的子树是平衡二叉树if (root == NULL)return true;// 如果不是空就去计算这个根节点 左子树和右子树的深度 并判断其相减的绝对值是否<=1int leftdepth = MaxDepth(root->left);int rightdepth = MaxDepth(root->right);if (abs(leftdepth - rightdepth) > 1)return false;// 每一个根结点(每一个根节点都代表一个子树)都要去判断是否是平衡二叉树return isBalanced(root->left) && isBalanced(root->right);
}

尽管上面我们的代码可以实现功能，但是我们的时间复杂度是O(N^2)。

这是因为我们的代码是采用的前序遍历二叉树，会有大量的重复计算——就比如，其实我们再调用第一次函数的时候，所有节点的左右子树的深度都被计算过了，但是我们仍然会进行重复计算。 这就导致我们的代码效率比较低下。

那我们是否可以做到优化呢？

其实是可以的，我们可以采用后序遍历二叉树。

从最后的左右子树开始计算其深度，并判断是否为平衡二叉树，如果是就返回深度，往上遍历，这样子处理，每个根节点的深度就只用被计算一次，并且遇到不是平衡二叉树的根节点，也可以及时退出递归。

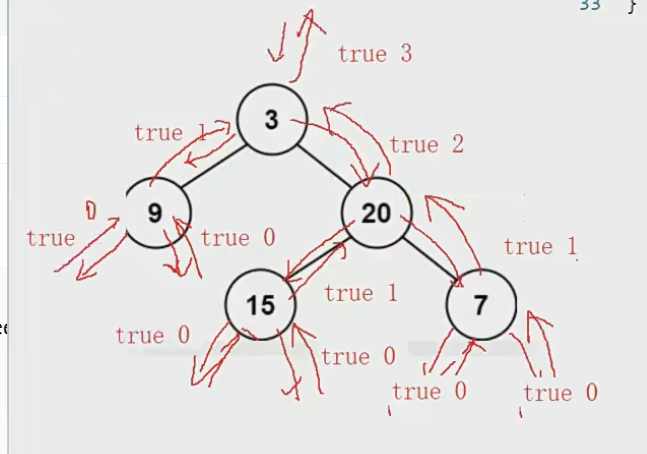
image-20240514012209623

注意了，这个过程是后序遍历实现的

思路讲完了，我们来实现一下代码：

优化后代码：

bool _isBalanced(struct TreeNode* root, int* pdepth)
{// 判断传进来的根节点是否是NULLif(root == NULL){*pdepth = 0;return true;}// 后序遍历 // 先递归左子树int leftdepth = 0; // 记录左子树的深度if(_isBalanced(root->left, &leftdepth) == false)return false; // 不是平衡二叉树就不用带上高度的计算了// 递归右子树int rightdepth = 0; //记录右子树的深度if(_isBalanced(root->right, &rightdepth) == false)return false; // 不是平衡二叉树就不用带上高度的计算了int gas = leftdepth - rightdepth;if(abs(gas) > 1)return false;// 走到这里 说明，当前节点是平衡二叉树，那就计算高度*pdepth = leftdepth > rightdepth ? leftdepth + 1 : rightdepth + 1;return true;
}bool isBalanced(struct TreeNode* root)  // 时间复杂度是O(N)
{//计算其每个左右子树的深度，并判断其是否为平衡二叉树// 为了提高效率使用后序遍历二叉树// 我们使用子函数去实现后序遍历int depth = 0;return _isBalanced(root, &depth); // 传第二个参数的目的是判断的同时，带高度 这样才能实现时间复杂度的优化
}

11.二叉树的构建和遍历（清华考研题）

题目：

二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

描述

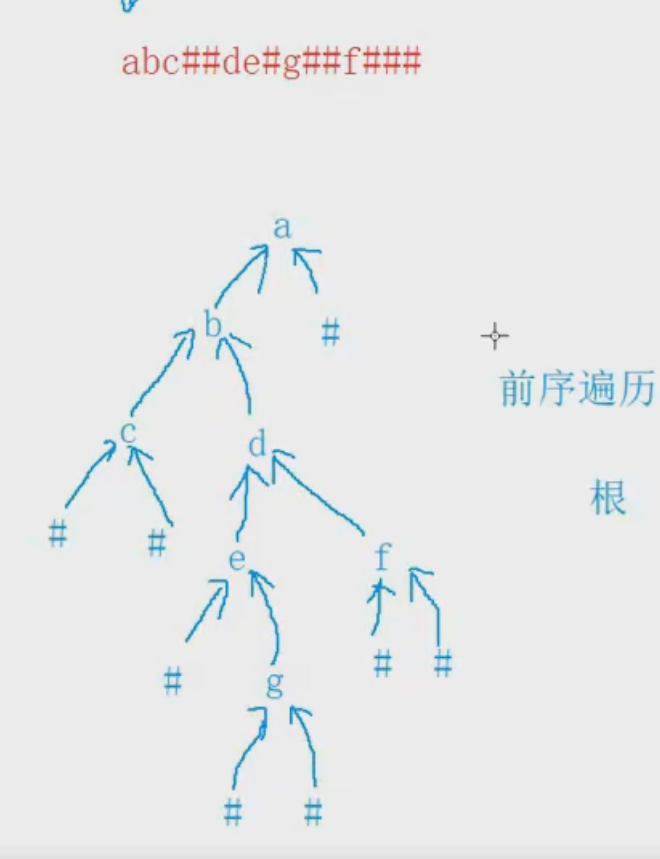
编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。

输入描述：

输入包括1行字符串，长度不超过100。

输出描述：

可能有多组测试数据，对于每组数据， 输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。 每个输出结果占一行。

示例1

输入：

abc##de#g##f###

输出：

c b e g d f a

思路：

  1. 先通过前序遍历构建出这个二叉树的。
  2. 然后再用中序遍历去访问这课二叉树

image-20240514094443879

代码：

#include <stdio.h>typedef struct TreeNode
{char val;struct TreeNode* left;struct TreeNode* right;
}TreeNode;void InOrder(TreeNode* root)
{if(root == NULL)return;// 中序遍历InOrder(root->left);printf("%c ", root->val);InOrder(root->right);
} TreeNode* CreateTree(char* str, int* pi)
{// 判断此时是否为NULL if(str[*pi] == '#'){(*pi)++;return NULL;}else {// 不为NULL就要构建节点TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));// 根据先序构建二叉树 【根——左子树——右子树】root->val = str[*pi];(*pi)++;root->left = CreateTree(str, pi); root->right = CreateTree(str, pi);return root;}
}int main() 
{// 让用户输入以先序遍历的字符串char str[100];scanf("%s", str);// 根据字符串去先序构建二叉树int i = 0;TreeNode* root = CreateTree(str, &i);// 为了让所有递归用的是同一个i 必须传地址// 中序遍历二叉树InOrder(root);return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/700114.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

汇昌联信：拼多多网店该如何开店?

汇昌联信：拼多多网店该如何开店?

拼多多网店的开设流程并不复杂&#xff0c;但需要细心和耐心去完成每一步。下面将详细阐述如何开设一家拼多多网店。 一、选择商品与定位 开设拼多多网店的第一步是确定你要销售的商品类型&#xff0c;这决定了你的目标客户群体和市场定位。你需要了解这些商品的市场需求、竞争…
阅读更多...
什么是CCRC？做什么用的？

什么是CCRC？做什么用的？

CCRC&#xff08;中国网络安全审查认证和市场监管大数据中心&#xff09;原名为中国网络安全审查技术与认证中心&#xff0c;也被称为中国信息安全认证中心&#xff08;ISCCC&#xff09;。 该中心是经中央机构编制委员会办公室批准成立的&#xff0c;其主要职责是依据国家法律…
阅读更多...
[图解]实现领域驱动设计译文暴露的问题04

[图解]实现领域驱动设计译文暴露的问题04

0 00:00:00,960 --> 00:00:03,020 今天我们继续说一下 1 00:00:03,460 --> 00:00:05,350 实现领域驱动设计 2 00:00:05,630 --> 00:00:08,120 译文里面暴露的问题 3 00:00:10,630 --> 00:00:14,740 前面三个视频&#xff0c;我们提到了第①句 4 00:00:15,550 -…
阅读更多...
vuerouter声明式导航

vuerouter声明式导航

声明式导航-跳转传参数 1.查询参数传参 语法&#xff1a;to /path?参数名值 2.对应页面组件接受传来的值 $router.query.参数名 2.动态路由传参 1.配置动态路由 2.配置导航连接 to/path/参数值 3.对应页面组件接收传递过来的值 #route.params.参数名 多个参数传递&…
阅读更多...
untiy 为预制体动态加载光照贴图

untiy 为预制体动态加载光照贴图

unity版本为2021.8 预制体不能携带光照贴图信息&#xff0c;只能我们自己准备了 多方查找加自己摸索终于找到了适合新版本的解决方案&#xff0c;直接贴代码 将这个脚本挂到预制体的最上级 using System.Collections; using System.Collections.Generic; using UnityEditor; …
阅读更多...
强化训练：day8（求最小公倍数、数组中的最⻓连续⼦序列、字⺟收集）

强化训练：day8（求最小公倍数、数组中的最⻓连续⼦序列、字⺟收集）

文章目录 前言1. 最小公倍数1.1 题目描述1.2 解题思路1.3 代码实现 2. 数组中的最⻓连续⼦序列2.1 题目描述2.2 解题思路2.3 代码实现 3. 字母收集3.1 题目描述3.2 解题思路3.3 代码实现 总结 前言 1. 最小公倍数   2. 数组中的最⻓连续⼦序列   3. 字⺟收集 1. 最小公倍数…
阅读更多...
【数据可视化01】matplotlib实例介绍2

【数据可视化01】matplotlib实例介绍2

目录 一、引言二、实例介绍1.箱线图2.热力图3.3D图 一、引言 接着上一文章【数据可视化01】matplotlib实例介绍1继续介绍matplotlib的实例。 二、实例介绍 在matplotlib中&#xff0c;常用的图形类型包括&#xff1a; 箱线图&#xff08;Box plot&#xff09;&#xff1a;用…
阅读更多...
[Java EE] 文件IO (二):文件内容读写-----数据流

[Java EE] 文件IO (二):文件内容读写-----数据流

&#x1f338;个人主页:https://blog.csdn.net/2301_80050796?spm1000.2115.3001.5343 &#x1f3f5;️热门专栏:&#x1f355; Collection与数据结构 (91平均质量分)https://blog.csdn.net/2301_80050796/category_12621348.html?spm1001.2014.3001.5482 &#x1f9c0;Java …
阅读更多...
Seal^_^【送书活动第4期】——《Web渗透测试技术》

Seal^_^【送书活动第4期】——《Web渗透测试技术》

Seal^_^【送书活动第4期】——《Web渗透测试技术》 一、参与方式二、本期推荐图书2.1 前 言2.2 关于本书2.3 本书读者2.4 图书简介2.5 作者荐语2.6 编辑推荐2.7 目 录 三、正版购买 掌握Web渗透测试技术&#xff0c;提高Web应用安全性。 一、参与方式 1、关注博主的账号。 2、点…
阅读更多...
Qt---项目的创建及运行

Qt---项目的创建及运行

一、创建第一个Qt程序 1. 点击创建项目后&#xff0c;选择项目路径以及给项目起名称 名称&#xff1a;不能有中文、不能有空格 路径&#xff1a;不能有中文路径 2. 默认创建有窗口类myWidget&#xff0c;基类有三种选择&#xff1a;QWidget、QMainWindow、QDialog 3. m…
阅读更多...
ssl证书免费申请指南

ssl证书免费申请指南

同学们可以私信我加入学习群&#xff01; 正文开始 前言一、购买证书二、创建证书三、 验证证书等待出现如下页面&#xff0c;说明申请成功&#xff1a; ![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/6b6c1dd11d4c467687318552da7cdbb2.png) 总结 前言 今天为大…
阅读更多...
企业必看：镭速教你如何测试内网文件传输效率和稳定问题

企业必看：镭速教你如何测试内网文件传输效率和稳定问题

在现代商业运作中&#xff0c;企业内部文件传输的效率和稳定性对于数据管理和业务流程极为重要。无论是远程工作还是团队协作&#xff0c;高效的文件传输都能显著提升工作效率。今天镭速小编就教你如何测试内网文件传输效率和稳定问题。 1、磁盘性能&#xff0c;即硬盘的读取和…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023