题4:变换阵型
【题目描述】
盛隆同学刚学完C++的二维数组和函数部分,于是他自己写了2个函数对二维数组进行练习。两个函数如下:
int n, a[1005][1005]; // 注意,这里的n和数组a是全局变量
void f1() {for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {int t = a[i][j];a[i][j] = a[j][i];a[j][i] = t;}}
}
void f2() {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n - i + 1; j++) {int t = a[i][j];a[i][j] = a[n-j+1][n-i+1];a[n-j+1][n-i+1] = t;}}
}
现给出一个 n x n 的矩阵 a,矩阵的行列下标均从 1 开始,也就是说矩阵中的第 i 行第 j 列的元素保存在 a[i][j] 中。
现在盛隆同学想要对矩阵 a 进行 Q 次操作,操作共有三种,参数分别如下:
- 1:调用函数 f1。
- 2:调用函数 f2。
- 3 x y:输出矩阵 a 目前第 x 行第 y 列的元素。
【输入】
第一行两个整数 n,Q,表示矩阵的大小和操作的次数。
接下来 n 行,每行 n 个整数,表示矩阵 a。
接下来 Q 行,每行一个操作,操作格式如题目描述。
【输出】
对于每个操作 3 x y,输出一行一个整数,表示矩阵 a 目前第 x 行第 y 列的元素。
【输入样例1】
3 3
1 2 3
4 5 6
7 8 9
1
2
3 1 2
【输出样例1】
8
样例解释
原矩阵经过 n 次操作后的矩阵如下:
9 8 7
6 5 4
3 2 1
所以 a[1][2]=8 。
【输入样例2】
4 4
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
1
3 1 2
2
3 2 3
【输出样例2】
5
10
【数据规模及约定】
对于20%的数据,没有操作一和操作二,只有操作三。
对于50%的数据,1 ≤ n ≤ 500 , 1 ≤ Q ≤ 100。
对于100%的数据,1 ≤ n ≤ 1000 , 1 ≤ Q ≤ 10000 , 0 ≤ a 𝑖𝑗 ≤ 109, , 1 ≤ x,y ≤n。
题目解析:
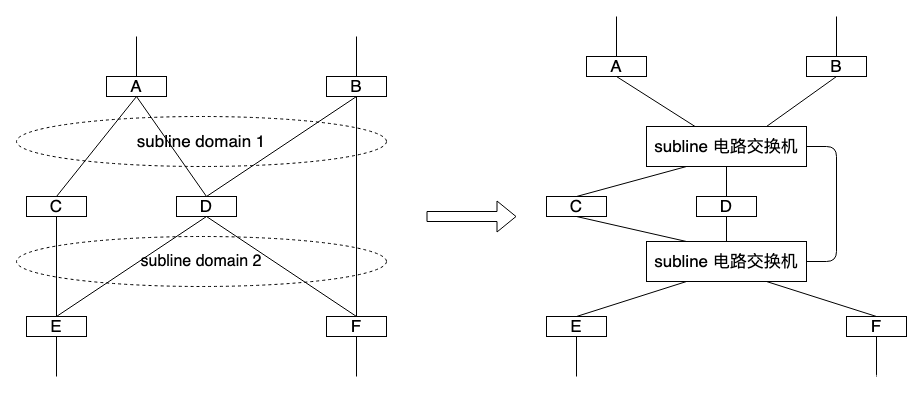
**根据题意,当读取到1或2后,分别会调用f1或f2函数后,矩阵将发生变化,页读取到3时,只需要输出当前矩阵状态下对应位置的值即可,所以重点要分析调用函数后矩阵的变化情况,如果直接用暴力必然拿不到满分,会超时。可以试着模拟一个6x6的矩阵,调用f1和f2函数让矩阵变化,可以将每一种矩阵当作一种图案,在当前矩阵图案下,有两条途径,可以调用f1函数或f2函数,可列出图表(如下图),发现如下规律:
1、如果连续调用同一函数,矩阵的会在两种图案中来回切换;
2、f1、f2交叉调用,各调用一次后会得到相同图案,反复交叉调用后发现只有四种图案,并且最先调用f1函数与最先调用f2函数所得到的矩阵图案刚好是相反的顺序;
因此,可以先将四种矩阵模拟出来存储起来,然后根据输入的情况直接读取对应的图案即可。
**
代码如下:
#include <bits/stdc++.h>
using namespace std;
int n,Q, a[1005][1005],m,aa[5][1005][1005],x1,x2;
void f1() {for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {int t = a[i][j];a[i][j] = a[j][i];a[j][i] = t;}}
}
void f2() {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n - i + 1; j++) {int t = a[i][j];a[i][j] = a[n - j + 1][n - i + 1];a[n - j + 1][n - i + 1] = t;}}
}int main() {cin >> n >> Q;for (int i = 1; i <= n; i++)for (int j = 1; j <= n; j++) cin >> a[i][j];int x, y;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)aa[0][i][j]=a[i][j];f1();for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)aa[1][i][j]=a[i][j];f2();for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)aa[3][i][j]=a[i][j];f1();for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)aa[2][i][j]=a[i][j];for (int k = 1; k <= Q; k++){cin >> m;if(m==1)x1=1-x1;else if(m==2)x2=2-x2;else {cin>>x>>y;cout<<aa[x1+x2][x][y]<<"\n";}}return 0;
}