文章目录
- 发现宝藏
- 【考生须知】
- 试题 A: 合数个数
- 试题 B : 含 2 天数
- 试题 C: 本质上升序列
- 试题 D: 迨尺天涯
- 试题 E: 玩具蛇
- 试题 F: 游园安排
- 试题 G: 画廊
- 试题 H: 奇偶覆盖
- 试题 I: 补给
- 试题 J: 蓝跳跳
发现宝藏
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【宝藏入口】。
【考生须知】
考试开始后, 选手首先下载题目, 并使用考场现场公布的解压密码解压试
考试时间为 4 小时。考试期间选手可汶览自己已经提交的答案, 被浏览的答案允许拷贝。时间截止后, 将无法继续提交或浏览答案。
对同一题目, 选手可多次提交答案, 以最后一次提交的答案为准。
选手必须通过浏览器方式提交自己的答案。选手在其它位置的作答或其它方式提交的答案无效。
试题包含 “结果填空” 和 “程序设计” 两种题型。
结果填空题: 要求选手根据题目描述直接填写结果。求解方式不限。不要求源代码。把结果填空的答案直接通过网页提交即可, 不要书写多余的内容。
程序设计题: 要求选手设计的程序对于给定的输入能给出正确的输出结果。考生的程序只有能运行出正确结果才有机会得分。
注意: 在评卷时使用的输入数据与试卷中给出的示例数据可能是不同的。选手的程序必须是通用的, 不能只对试卷中给定的数据有效。
所有源码必须在同一文件中。调试通过后,拷贝提交。
注意: 不要使用 package 语句。
注意: 选手代码的主类名必须为: Main, 否则会被判为无效代码。
注意: 如果程序中引用了类库, 在提交时必须将 import 语句与程序的其他部分同时提交。只允许使用 Java 自带的类库。
试题 A: 合数个数
本题总分: 5 分
【问题描述】
一个数如果除了 1 和自己还有其他约数, 则称为一个合数。例如: 1 , 2 , 3 1,2,3 1,2,3不是合数, 4,6 是合数。
请问从 1 到 2020 一共有多少个合数。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 B : 含 2 天数
本题总分: 5 分
【问题描述】
小蓝特别喜欢 2 , 今年是公元 2020 年, 他特别高兴, 因为每天日历上都可以看到 2。
如果日历中只显示年月日, 请问从公元 1900 年 1 月 1 日到公元 9999 年 12 月 31 日, 一共有多少天日历上包含 2。即有多少天中年月日的数位中包含数字 2 。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 C: 本质上升序列
本题总分: 10 分
小蓝特别喜欢单调递增的事物。
在一个字符串中, 如果取出若干个字符, 将这些字符按照在字符串中的顺序排列后是单调递增的, 则成为这个字符串中的一个单调递增子序列。
例如, 在字符串 lanqiao 中, 如果取出字符 n n n 和 q q q, 则 n q n q nq 组成一个单调递增子序列。类似的单调递增子序列还有 1 n q 1 \mathrm{nq} 1nq 、 i、ano 等等。
小蓝发现, 有些子序列虽然位置不同, 但是字符序列是一样的, 例如取第二个字符和最后一个字符可以取到 ao, 取最后两个字符也可以取到 ao。小蓝认为他们并没有本质不同。
对于一个字符串, 小蓝想知道, 本质不同的递增子序列有多少个?
例如, 对于字符串 lanqiao, 本质不同的递增子序列有 21 个。它们分别是 1 、 a 、 n 、 q 、 i 、 o 、 1 n 、 a n 、 1 q 、 a q 、 n q 、 a i 、 1 o 、 a o 、 n o 、 i o v 1 n q 、 1 、 a 、 n 、 q 、 i 、 o 、 1 n 、 a n 、 1 q 、 a q 、 n q 、 a i 、 1 o 、 a o 、 n o 、 i o v 1 n q 、 1、a、n、q、i、o、1n、an、1q、aq、nq、ai、1o、ao、no、iov1nq、 anq, Ino, ano, aio.
请问对于以下字符串 (共 200 个小写英文字母, 分四行显示): (如果你把以下文字复制到文本文件中, 请务必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 inc.txt, 内容与下面的文本相同)
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij gihhfgdemxvicfauachlifhafpdccfseflcdgjncadfclvfmad vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 D: 迨尺天涯
本题总分: 10 分
【问题描述】
皮亚诺曲线是一条平面内的曲线。
下图给出了皮亚诺曲线的 1 阶情形, 它是从左下角出发, 经过一个 3 × 3 3 \times 3 3×3 的方格中的每一个格子, 最终到达右上角的一条曲线。

设每个格子的边长为 1 , 在上图中, 有的相邻的方格 (四相邻) 在皮亚诺曲线中也是相邻的, 在皮亚诺曲线上的距离是 1, 有的相邻的方格在皮亚诺曲线中不相邻, 距离大于 1 。
例如, 正中间方格的上下两格都与它在皮亚诺曲线上相邻, 距离为 1 , 左右两格都与它在皮亚诺曲线上不相邻, 距离为 3 。
下图给出了皮亚诺曲线的 2 阶情形, 它是经过一个 3 2 × 3 2 3^2 \times 3^2 32×32 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。
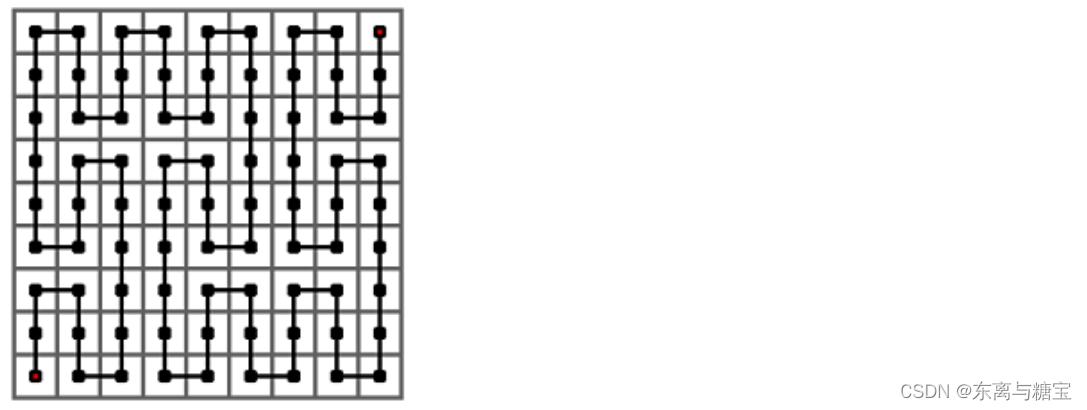
设每个格子的边长为 1 , 在上图中, 有的相邻的方格(四相邻)在皮亚诺曲线中也是相邻的, 在皮亚诺曲线上的距离是 1, 有的相邻的方格在皮亚诺曲线中不相邻, 距离大于 1 。
例如, 正中间方格的上下两格都与它在皮亚诺曲线上相邻, 距离为 1 , 左右两格都与它在皮亚诺曲线上不相邻, 距离为 3 。
下图给出了皮亚诺曲线的 2 阶情形, 它是经过一个 3 2 × 3 2 3^{2} \times 3^{2} 32×32 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。
下图给出了皮亚诺曲线的 3 阶情形, 它是经过一个 3 3 × 3 3 3^{3} \times 3^{3} 33×33 的方格中的每一个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发, 最终到达右上角。
小蓝对于相邻的方格在皮亚诺曲线上的相邻关系很好奇, 他想知道相邻的方格在曲线上的距离之和是多少。
例如, 对于 1 阶皮亚诺曲线, 距离和是 24 , 有 8 对相邻的方格距离为 1 , 2 对相邻的方格距离为 3,2 对相邻的方格距离为 5 。
再如, 对于 2 阶皮亚诺曲线, 距离和是 816 。
请求出对于 12 阶皮亚诺曲线, 距离和是多少。
提示: 答案不超过 1 0 18 10^{18} 1018 。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 E: 玩具蛇
本题总分: 15 分
【问题描述】
小蓝有一条玩具蛇, 一共有 16 节, 上面标着数字 1 至 16 。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4 4 \times 4 4×4 的方格盒子, 用于存放玩具蛇, 盒子的方格上依次标着字母 A 到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现, 有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:
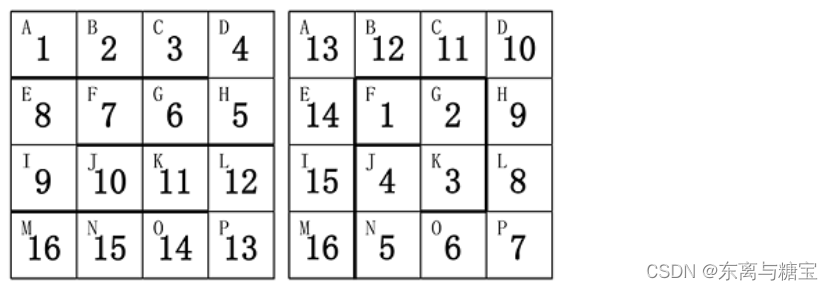
请帮小蓝计算一下, 总共有多少种不同的方案。如果两个方案中, 存在玩具蛇的某一节放在了盒子的不同格子里, 则认为是不同的方案。
【答案提交】
这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。
试题 F: 游园安排
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 15 分
【问题描述】
L \mathrm{L} L 星球游乐园非常有趣, 吸引着各个星球的游客前来游玩。小蓝是 L \mathrm{L} L 星球游乐园的管理员。
为了更好的管理游乐园, 游乐园要求所有的游客提前预约, 小蓝能看到系统上所有预约游客的名字。每个游客的名字由一个大写英文字母开始, 后面跟 0 个或多个小写英文字母。游客可能重名。
小蓝特别喜欢递增的事物。今天, 他决定在所有预约的游客中, 选择一部分游客在上午游玩, 其他的游客都在下午游玩, 在上午游玩的游客要求按照预约的顺序排列后, 名字是单调递增的, 即排在前面的名字严格小于排在后面的名字。
一个名字 A A A 小于另一个名字 B B B 是指:存在一个整数 i i i, 使得 A A A 的前 i i i 个字母与 B B B 的前 i i i 个字母相同, 且 A A A 的第 i + 1 i+1 i+1 个字母小于 B B B 的第 i + 1 i+1 i+1 个字母。(如果 A A A 不存在第 i + 1 i+1 i+1 个字母且 B B B 存在第 i + 1 i+1 i+1 个字母, 也视为 A A A 的第 i + 1 i+1 i+1 个字母小于 B B B 的第 i + 1 i+1 i+1 个字母)
作为小蓝的助手, 你要按照小蓝的想法安排游客, 同时你又希望上午有尽量多的游客游玩, 请告诉小蓝让哪些游客上午游玩。如果方案有多种, 请输出上午游玩的第一个游客名字最小的方案。如果此时还有多种方案, 请输出第一个游客名字最小的前提下第二个游客名字最小的方案。如果仍然有多种, 依此类推选择第三个、第四个……游客名字最小的方案。
【输入格式】
输入包含一个字符串, 按预约的顺序给出所有游客的名字, 相邻的游客名字之间没有字符分隔。
【输出格式】
按预约顺序输出上午游玩的游客名单, 中间不加任何分隔字符。
【样例输入】
WoAiLanQiaoBei
【样例输出】
AiLanQiao
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测数据, 输入的总长度不超过 20 个字母。
对于 50 % 50 \% 50% 的评测数据, 输入的总长度不超过 300 个字母。
对于 70 % 70 \% 70% 的评测数据, 输入的总长度不超过 10000 个字母。
对于所有评测数据, 每个名字的长度不超过 10 个字母, 输入的总长度不超过 1000000 个字母.
试题 G: 画廊
时间限制: 1.0 s 1.0 \mathrm{~s} 1.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 20 分
【问题描述】
小蓝办了一个画展, 在一个画廊左右两边陈列了他自己的作品。为了使画展更有意思, 小蓝没有等距陈列自己的作品, 而是按照更有艺术感的方式陈列。在画廊的左边陈列了 L L L 幅作品, 在画廊的右边陈列了 R R R 幅作品, 左边的作品距离画廊的起点依次为 u 1 , u 2 , ⋯ , u L u_{1}, u_{2}, \cdots, u_{L} u1,u2,⋯,uL, 右边的作品距离画廊起点依次为 v 1 , v 2 , ⋯ v_{1}, v_{2}, \cdots v1,v2,⋯, v R ∘ v_{R} \circ vR∘
每周, 小蓝要整理一遍自己的每一幅作品。整理一幅作品的时间是固定的,但是要带着沉重的工具。从一幅作品到另一幅作品之间的距离为直线段的长度。
小蓝从画廊的起点的正中央(左右两边的中点)出发, 整理好每一幅画,最终到达画廊的终点的正中央。已知画廊的宽为 w 。 w_{\text {。 }} w。
请问小蓝最少带着工具走多长的距离?
【输入格式】
输入的第一行包含四个整数 L , R , d , w L, R, d, w L,R,d,w, 表示画廊左边和右边的作品数量,以及画廊的长度和宽度。
第二行包含 L L L 个正整数 u 1 , u 2 , ⋯ , u L u_{1}, u_{2}, \cdots, u_{L} u1,u2,⋯,uL, 表示画廊左边的作品的位置。
第三行包含 R R R 个正整数 v 1 , v 2 , ⋯ , v R v_{1}, v_{2}, \cdots, v_{R} v1,v2,⋯,vR, 表示画廊右边的作品的位置。
【输出格式】
输出一个实数, 四舍五入保留两位小数, 表示小蓝最少带着工具走的距离。
【样例输入】
3 3 10 2 \begin{array}{llll}3&3&10&2\end{array} 33102
1 3 8 \begin{array}{llll}1&3&8\end{array} 138
2 4 6 \begin{array}{llll}2&4&6\end{array} 246
【样例输出】
14.71 \begin{array}{llll}14.71\end{array} 14.71
【样例说明】
小蓝从起点开始, 首先到达左边第一幅作品 (走动距离 2 \sqrt{2} 2 ), 然后到达左边第二幅作品 (走动距离 2), 然后到达右边第一幅作品 (走动距离 5 \sqrt{5} 5 ), 然后到达右边第二幅和第三幅作品 (走动距离 2 和 2), 然后到达左边第三幅作品 (走动距离 2 2 2 \sqrt{2} 22 ), 最后到达画廊终点 (走动距离 5 \sqrt{5} 5 )。
总共距离为 2 + 2 + 5 + 2 + 2 + 2 2 + 5 ≈ 14.71 \sqrt{2}+2+\sqrt{5}+2+2+2 \sqrt{2}+\sqrt{5} \approx 14.71 2+2+5+2+2+22+5≈14.71 。
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例, 1 ≤ L , R ≤ 10 , 1 ≤ d ≤ 100 , 1 ≤ w ≤ 100 1 \leq L, R \leq 10,1 \leq d \leq 100,1 \leq w \leq 100 1≤L,R≤10,1≤d≤100,1≤w≤100 。
对于 70 % 70 \% 70% 的评测用例, 1 ≤ L , R ≤ 100 , 1 ≤ d ≤ 1000 , 1 ≤ w ≤ 1000 1 \leq L, R \leq 100,1 \leq d \leq 1000,1 \leq w \leq 1000 1≤L,R≤100,1≤d≤1000,1≤w≤1000 。
对于所有评测用例, 1 ≤ L , R ≤ 500 , 1 ≤ d ≤ 100000 , 1 ≤ w ≤ 100000 1 \leq L, R \leq 500,1 \leq d \leq 100000,1 \leq w \leq 100000 1≤L,R≤500,1≤d≤100000,1≤w≤100000, 0 ≤ u 1 < u 2 < ⋯ < u L ≤ d , 0 ≤ v 1 < v 2 < ⋯ < v R ≤ d 。 0 \leq u_{1}<u_{2}<\cdots<u_{L} \leq d, 0 \leq v_{1}<v_{2}<\cdots<v_{R} \leq d 。 0≤u1<u2<⋯<uL≤d,0≤v1<v2<⋯<vR≤d。
试题 H: 奇偶覆盖
时间限制: 2.0 s 2.0 \mathrm{~s} 2.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 20 分
【问题描述】
在平面内有一些矩形, 它们的两条边都平行于坐标轴。
我们称一个点被某个矩形覆盖, 是指这个点在矩形的内部或者边界上。
请问, 被奇数个矩形覆盖和被偶数 ( ≥ 2 ) (\geq 2) (≥2) 个矩形覆盖的点的面积分别是多少?
【输入格式】
输入的第一行包含一个整数 n n n, 表示矩形的个数。
接下来 n n n 行描述这些矩形, 其中第 i i i 行包含四个整数 l i , b i , r i , t i l_{i}, b_{i}, r_{i}, t_{i} li,bi,ri,ti, 表示矩形的两个对角坐标分别为 ( l i , b i ) , ( r i , t i ) \left(l_{i}, b_{i}\right),\left(r_{i}, t_{i}\right) (li,bi),(ri,ti) 。
【输出格式】
输出两行。
第一行包含一个整数, 表示被奇数个矩形覆盖的点的面积。
第二行包含一个整数, 表示被偶数 ( ≥ 2 ) (\geq 2) (≥2) 个矩形覆盖的点的面积。
【样例输入】
3 \begin{array}{llll}3\end{array} 3
1 1 3 3 \begin{array}{llll}1&1&3&3\end{array} 1133
2 2 4 4 \begin{array}{llll}2&2&4&4\end{array} 2244
3 3 5 5 \begin{array}{llll}3&3&5&5\end{array} 3355
【样例输出】
8 \begin{array}{llll}8\end{array} 8
2 \begin{array}{llll}2\end{array} 2
【评测用例规模与约定】
对于 20 % 20 \% 20% 的评测用例, 1 ≤ n ≤ 10 , 0 ≤ l i < r i ≤ 100 , 0 ≤ b i < t i ≤ 100 1 \leq n \leq 10,0 \leq l_{i}<r_{i} \leq 100,0 \leq b_{i}<t_{i} \leq 100 1≤n≤10,0≤li<ri≤100,0≤bi<ti≤100 。
对于 40 % 40 \% 40% 的评测用例, 1 ≤ n ≤ 1000 , 0 ≤ l i < r i ≤ 100 , 0 ≤ b i < t i ≤ 100 1 \leq n \leq 1000,0 \leq l_{i}<r_{i} \leq 100,0 \leq b_{i}<t_{i} \leq 100 1≤n≤1000,0≤li<ri≤100,0≤bi<ti≤100 。
对于 60 % 60 \% 60% 的评测用例, 1 ≤ n ≤ 10000 , 0 ≤ l i < r i ≤ 1000 , 0 ≤ b i < t i ≤ 1000 1 \leq n \leq 10000,0 \leq l_{i}<r_{i} \leq 1000,0 \leq b_{i}<t_{i} \leq 1000 1≤n≤10000,0≤li<ri≤1000,0≤bi<ti≤1000 。
对于 80 % 80 \% 80% 的评测用例, 1 ≤ n ≤ 100000 , 0 ≤ l i < r i ≤ 100000 , 0 ≤ b i < t i ≤ 1 \leq n \leq 100000,0 \leq l_{i}<r_{i} \leq 100000,0 \leq b_{i}<t_{i} \leq 1≤n≤100000,0≤li<ri≤100000,0≤bi<ti≤ 100000 。
对于所有评测用例, 1 ≤ n ≤ 100000 , 0 ≤ l i < r i ≤ 1 0 9 , 0 ≤ b i < t i ≤ 1 0 9 1 \leq n \leq 100000,0 \leq l_{i}<r_{i} \leq 10^{9}, 0 \leq b_{i}<t_{i} \leq 10^{9} 1≤n≤100000,0≤li<ri≤109,0≤bi<ti≤109 。
试题 I: 补给
时间限制: 3.0 s 3.0 \mathrm{~s} 3.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 25 分
【问题描述】
小蓝是一个直升飞机驾驶员, 他负责给山区的 n n n 个村庄运送物资。每个月,他都要到每个村庄至少一次, 可以多于一次, 将村座需要的物资运送过去。每个村庄都正好有一个直升机场, 每两个村庄之间的路程都正好是村庄之间的直线距离。
由于直升机的油箱大小有限, 小蓝单次飞行的距离不能超过 D D D 。每个直升机场都有加油站, 可以给直升机加满油。
每个月, 小蓝都是从总部出发, 给各个村庄运送完物资后回到总部。如果方便,小蓝中途也可以经过总部来加油。
总部位于编号为 1 的村庄。
请问, 要完成一个月的任务, 小蓝至少要飞行多长距离?
【输入格式】
输入的第一行包含两个整数 n , D n, D n,D, 分别表示村庄的数量和单次飞行的距离。
接下来 n n n 行描述村庄的位置, 其中第 i i i 行两个整数 x i , y i x_{i}, y_{i} xi,yi, 表示编号为 i i i 的村庄的坐标。村庄 i i i 和村庄 j j j 之间的距离为 ( x i − x j ) 2 + ( y i − y j ) 2 \sqrt{\left(x_{i}-x_{j}\right)^{2}+\left(y_{i}-y_{j}\right)^{2}} (xi−xj)2+(yi−yj)2 。
【输出格式】
输出一行, 包含一个实数, 四舍五入保留正好 2 位小数, 表示答案。
【样例输入】
4 10 \begin{array}{llll}4&10\end{array} 410
1 1 \begin{array}{llll}1&1\end{array} 11
5 5 \begin{array}{llll}5&5\end{array} 55
1 5 \begin{array}{llll}1&5\end{array} 15
【样例输出】
16.00 \begin{array}{llll}16.00\end{array} 16.00
【样例说明】
四个村座形成一个正方形的形状。
【样例输入】
4 6 \begin{array}{llll}4&6\end{array} 46
1 1 \begin{array}{llll}1&1\end{array} 11
4 5 \begin{array}{llll}4&5\end{array} 45
8 5 \begin{array}{llll}8&5\end{array} 85
1 11 \begin{array}{llll}1&11\end{array} 111
【样例输出】
28.00 \begin{array}{llll}28.00\end{array} 28.00
【样例说明】
补给顺序为 1 → 2 → 3 → 4 → 3 → 2 → 1 1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 3 \rightarrow 2 \rightarrow 1 1→2→3→4→3→2→1 。
【评测用例规模与约定】
对于所有评测用例, 1 ≤ n ≤ 20 , 1 ≤ x i , y i ≤ 1 0 4 , 1 ≤ D ≤ 1 0 5 1 \leq n \leq 20,1 \leq x_{i}, y_{i} \leq 10^{4}, 1 \leq D \leq 10^{5} 1≤n≤20,1≤xi,yi≤104,1≤D≤105 。
试题 J: 蓝跳跳
时间限制: 10.0 s 10.0 \mathrm{~s} 10.0 s 内存限制: 512.0 M B 512.0 \mathrm{MB} 512.0MB 本题总分: 25 分
【问题措述】
小蓝制作了一个机器人, 取名为蓝跳跳, 因为这个机器人走路的时候基本靠跳跃。
蓝跳跳可以跳着走, 也可以掉头。蓝跳跳每步跳的距离都必须是整数, 每步可以跳不超过 k k k 的长度。由于蓝跳跳的平衡性设计得不太好, 如果连续两次都是跳跃, 而且两次跳跃的距离都至少是 p p p, 则蓝跳跳会掠倒, 这是小蓝不愿意看到的。
小蓝接到一个特别的任务, 要在一个长为 L L L 舞台上展示蓝跳跳。小蓝要控制蓝跳跳从舞台的左边走到右边, 然后掉头, 然后从右边走到左边, 然后掉头,然后再从左边走到右边, 然后掉头, 再从右边走到左边, 然后掉头, 如此往复。
为了让观者不至于太无趣, 小蓝决定让蓝跳跳每次用不同的方式来走。小蓝将蓝跳跳每一步跳的距离记录下来, 按顺序排成一列, 显然这一列数每个都
不超过 k k k 且和是 L 。 L_{\text {。 }} L。 这样走一趟就会出来一列数。如果两列数的长度不同, 或者两列数中存在一个位置数值不同, 就认为是不同的方案。
请问蓝跳跳在不接倒的前提下, 有多少种不同的方案从舞台一边走到另一边。
【输入格式】
输入一行包含三个整数 k , p , L k, p, L k,p,L 。
【输出格式】
输出一个整数, 表示答案。答案可能很大, 请输出答案除以 20201114 的余数。
【样例输入】
3 2 5 \begin{array}{llll}3&2&5\end{array} 325
【样例输出】
9 \begin{array}{llll}9\end{array} 9
【样例说明】
蓝跳跳有以下 9 种跳法:
- 1 + 1 + 1 + 1 + 1 1+1+1+1+1 1+1+1+1+1
- 1 + 1 + 1 + 2 1+1+1+2 1+1+1+2
- 1 + 1 + 2 + 1 1+1+2+1 1+1+2+1
- 1 + 2 + 1 + 1 1+2+1+1 1+2+1+1
- 2 + 1 + 1 + 1 2+1+1+1 2+1+1+1
- 2 + 1 + 2 2+1+2 2+1+2
- 1 + 1 + 3 1+1+3 1+1+3
- 1 + 3 + 1 1+3+1 1+3+1
- 3 + 1 + 1 3+1+1 3+1+1
【样例输入】
5 3 10 \begin{array}{llll}5 & 3 & 10\end{array} 5310
【样例输出】
397 \begin{array}{llll}397\end{array} 397
【评测用例规模与约定】
对于 30 % 30 \% 30% 的评测用例, 1 ≤ p ≤ k ≤ 50 , 1 ≤ L ≤ 1000 1 \leq p \leq k \leq 50,1 \leq L \leq 1000 1≤p≤k≤50,1≤L≤1000 。
对于 60 % 60 \% 60% 的评测用例, 1 ≤ p ≤ k ≤ 50 , 1 ≤ L ≤ 1 0 9 1 \leq p \leq k \leq 50,1 \leq L \leq 10^{9} 1≤p≤k≤50,1≤L≤109 。
对于 80 % 80 \% 80% 的评测用例, 1 ≤ p ≤ k ≤ 200 , 1 ≤ L ≤ 1 0 18 1 \leq p \leq k \leq 200,1 \leq L \leq 10^{18} 1≤p≤k≤200,1≤L≤1018 。
对于所有评测用例, 1 ≤ p ≤ k ≤ 1000 , 1 ≤ L ≤ 1 0 18 1 \leq p \leq k \leq 1000,1 \leq L \leq 10^{18} 1≤p≤k≤1000,1≤L≤1018 。


![【学习笔记】C++每日一记[20240513]](https://img-blog.csdnimg.cn/direct/f1651c6ec3a043bea390f94075a34654.png)