程序设计：控制台输出二叉树二叉树的形象显示-编程知识

初级代码游戏的专栏介绍与文章目录-CSDN博客

我的github：codetoys，所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。

这些代码大部分以Linux为目标但部分代码是纯C++的，可以在任何平台上使用。

本文指导你编写一个输出到字符控制台的形象的二叉树展示。

一般的Tree显示方式

理想的显示方式

实现方法

计算显示位置

输出数据

计算子树宽度的代码

设置显示位置的代码

输出数据的代码

一般的Tree显示方式

编写二叉树算法时调试是很头疼的，如何显示成一目了然的树结构呢？以目录树方式显示当然比较简单，类似windows控制台的Tree命令的效果：

这种输出只需要正确计算节点的缩进级别就可以了，用一个递归函数很容易就实现了。

但是这种输出方式并不方便查看，不容易直接看到两个子节点。而我们一般讲解二叉树的时候都是横向排版，两个子节点排在父节点下面的同一行。

理想的显示方式

理想的显示方式如下图所示：

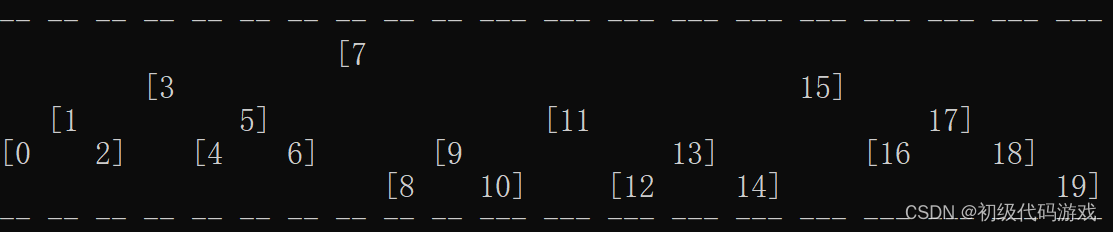
这就是程序的实际输出效果，左子节点左边有个“[”，右子节点右边有个“]”，这样每一组子节点就一目了然，左子树整个都显示在父节点的左边，右子树整个都显示在父节点右边。

由于我们的目的不是做完美的界面，所以不会考虑ncurse库这种能随意绘制的方式（如果这样不如直接用图形界面了），我们只考虑printf和cout的能力。

实现方法

要想实现这种效果，需要分两步来做：

计算整个左子树的宽度，从而确定节点显示位置
根据计算好的显示位置自上而下输出数据

计算显示位置

计算显示位置是个比较复杂的事情，因为每个节点的显示宽度是不确定的，需要预先确定每个节点的宽度，然后根据结构计算正确的位置，如果子节点缺失，没必要占用显示空间。

既然这么复杂，我们可以把问题拆开，把计算精确位置留给第二步，把每个节点当成一个格子，这一步只计算格子位置。

计算出的格子位置如何保存呢？这就需要一个表格，这个表格的行列数刚好容纳整个二叉树。仔细观察一下上面的输出示例图形，每一个节点都独立占据一列，左子树的宽度就是左子树的总节点数，因此表格的列数就是总的节点数，行数就是树的深度。

这样很容易预先申请一个二维数组，然后根据计算出的位置设置里面的值，最后将这个二维数组输出就可以了。

输出数据

经过上一步，输出数据已经在二维数组里，如何显示就比较容易了。只需要预先计算一下每列的最大显示宽度，然后逐个输出就可以了。

当然为了实现这个功能，最好有一些包装类，以简化操作。

计算子树宽度的代码

这只是示意代码：

	//获取节点总数，包括自身T_SHM_SIZE _check_get_count(T_SIZE h){//thelog << h << endi;T_SIZE n = 0;if (_check_is_data_node(h)){++n;//thelog << h << " " << TREE_NODE::at(h).hLeft<<" "<< TREE_NODE::at(h).hRight << endi;n += _check_get_count(TREE_NODE::at(h).hLeft);n += _check_get_count(TREE_NODE::at(h).hRight);}else{//thelog << "NULL" << endi;}return n;}

解释一下这个代码：

T_SIZE h 就是节点的指针或者句柄，这里实际上是位置索引。

_check_is_data_node(h) 判断一个位置是否是有效位置，相当于判断是不是空指针。

TREE_NODE::at(h) 获取位置上的节点对象的引用。

TREE_NODE::at(h).toString2(left) 这个代码获得节点的显示字符串，参数控制是否是左节点，左节点添加“[”，右节点添加“]”。

基本逻辑就是：

如果不是有效节点，返回0

否则返回1+左节点树的总节点数+右节点数的总节点数

显然这是一个递归函数。

设置显示位置的代码

上面的函数获得的就是子树的宽度（与节点总数相同），将其设置到表格里就可以了：

	//树形显示，px为偏移量，左边元素数void _check_show_tree(Table& table, T_SIZE h, bool left = true, T_SIZE line = 0, T_SIZE px = 0){//thelog << h << " " << line << " " << px << endi;if (!_check_is_data_node(h)){//thelog << "空" << endi;return;}T_SIZE leftCount = _check_get_count(TREE_NODE::at(h).hLeft);//thelog << "leftCount " << leftCount << endi;T_SIZE pos = px + leftCount;table.SetData(line, pos, TREE_NODE::at(h).toString2(left));//设置自身数据//thelog << "TREE_NODE::at(h).hLeft " << TREE_NODE::at(h).hLeft << endi;_check_show_tree(table, TREE_NODE::at(h).hLeft, true, line + 1, px);//处理左子项//thelog << "TREE_NODE::at(h).hRight " << TREE_NODE::at(h).hRight << endi;_check_show_tree(table, TREE_NODE::at(h).hRight, false, line + 1, pos + 1);//处理右子项}

解释一下这个代码：

Table是个包装好的类，能通过table.SetData()直接对某个位置设置值。

这当然也是一个递归函数。

输出数据的代码

第一步，计算每个列的最大宽度

第二步，按照每个列的最大宽度输出每个字段，为了格式整齐，一定要用空格来填补，不可以用tab。数据中最好不要有tab、回车换行之类的东西，也不要有中文。

这两步不算很复杂，稍微有点耐心就能写好了，算不上一个算法课题。我这里用的是已经包装好的通用类Table：

Table table;
rbtree._check_show_tree(table, rbtree.tree_head->hHead);
thelog << endl << table.MakeTextTable() << endi;

rbtree是红黑树对象。

table.MakeTextTable()把整个表格转换为文本表格。这个类还有些别的功能，比如转换为html的表格或者生成JS更新数据的脚本。我会在后续整理出这个代码（捆绑了太多特殊需要，需要删减）。

(这里是结束)