文章目录
- 一.摘要
- 二、相关工作 , 背景(gs)
- 三、基于图像的三维高斯预测
- 3.1 双视图图像编码器(解决尺度模糊性)
- 3.2 (像素对齐的)高斯参数预测
- 四、实验效果
论文:《pixelSplat: 3D Gaussian Splats from Image Pairs for Scalable Generalizable 3D Reconstruction》
地址:https://arxiv.org/pdf/2312.12337
代码:https://github.com/dcharatan/pixelsplat
作者:MIT, SFU
一.摘要
pixelSplat是一个前馈模型,能够从两张图像中,重建(由三维高斯原语参数化的)三维辐射场。其中, Epipolar line,也就是极线用于添加场景的深度(尺度)信息;为了克服稀疏和局部支持表示所固有的局部极小值,pixelSplat为3D预测了密集概率分布,并从中采样高斯均值。论文采用 重参数化的技巧使采样可微,可通过GS 反向传播梯度。在现实世界的RealEstate10k和ACID 数据集上进行基准测试,表现超过了最先进的 light field transformers,并加速渲染2.5个数量级,得到可解释和可编辑的三维辐射场。
二、相关工作 , 背景(gs)
单一场景的新视角合成。 在神经渲染[50]和神经场[29,42,57]领域的进步已经彻底改变了三维重建和来自姿态图像集合的新视图合成。最近的方法通常通过通过可微渲染器反向传播图像空间光度误差来创建3D场景表示。早期的方法采用体素网格和学习的渲染技术[27,31,40]。最近,神经场[2,28,29,57]和体渲染[27,29,49]已经成为事实上的标准。然而,这些方法的一个关键障碍是它们的高计算需求,因为渲染通常需要对每条射线的神经场进行几十个查询。Tensorf,Plenoxels,InstantNGP等离散的数据结构可以加速的渲染,但在高分辨率下不能实现实时渲染。三维高斯喷splats[19]通过使用三维高斯表示辐射场来解决这个问题,可以通过栅格化有效地渲染。然而,所有的单场景优化方法都需要数十幅图像来实现高质量的新视图合成。pixelSplat 仅用两张图像在一个单一的向前传递中训练神经网络,来估计一个三维高斯表示的参数。
基于先验的三维重建与视图合成。 可推广的新的视图合成寻求使三维重建和新的视图合成仅从少量的图像每个场景。如果代理几何(例如,深度图)可用,机器学习可以与基于图像的渲染[1,22,36,56]相结合,以产生令人信服的结果。神经网络也可以被训练为直接回归多平面图像的小基线新视图合成[45,53,60,61]。然而,大基线的新视图合成需要完整的3D表示。早期基于神经场[32,41]的方法在单个潜在编码3D场景,因此仅限于单对象场景。通过像素对齐的特征[14,23,39,52,58]或Transformer[35,54]保持端到端局部性和编码器和场景表示之间的位移等方差,能够泛化到无界场景。受经典的多视图立体几何的启发,神经网络也与代价体相结合,以匹配跨视图[5,7,18,26]的特征。虽然上述方法以符号距离或辐射场的形式推断出可解释的3D表示,但最近的 light field transformers 利用可解释性更有利于更快地渲染[10,37,43,46,47]
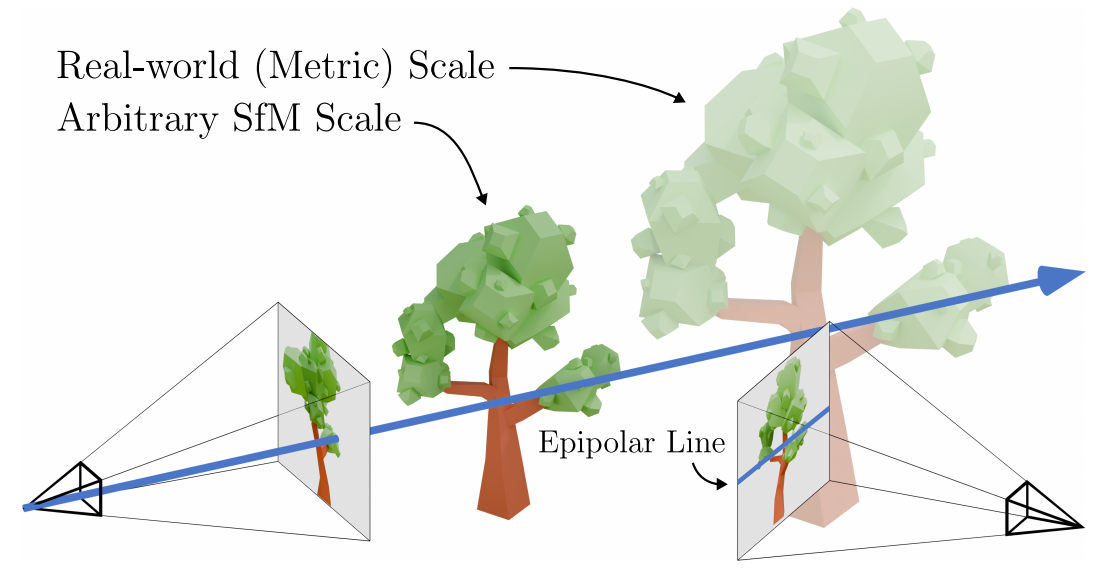
机器学习中多视图几何的尺度模糊性。先前的工作已经认识到了场景尺度模糊性的挑战。在单目深度估计中,最先进的模型依赖于复杂的尺度不变深度损失[11,13,33,34]。在新的视图合成中,最近在真实世界数据上训练的单图像三维扩散模型根据深度统计的启发式方法重新调整三维场景,并将其编码器设置在场景尺度[4,38,51]上。pixelSplat构建了一个多视图编码器,可以推断场景的尺度。具体使用一个epipolar transformer来实现这一点,它可以找到交叉视图像素对应,并将它们与位置编码的深度值相关联
Epipolar线 是在一个相机中观察到的点对应于另一个相机中的可能位置形成的线。

背景:
3D-GS将三维场景参数化为一组三维高斯基元,每个都有一个平均 µk、协方差 Σk、不透明度 αk和球谐系数 Sk。这些原语参数化了底层场景的三维辐射场,并可以被渲染以产生新的视图。
局部极小值。用原语拟合函数的一个关键挑战是它们对局部极小值的敏感性。三维-GS模型的拟合与高斯混合模型的拟合密切相关,其中我们寻找一组高斯的参数,以使得一组样本的似然最大化。这个问题是著名的非凸问题,通常用期望最大化(EM)算法来解决。可是,EM算法仍然存在局部最小的问题,不适用于inverse graphics,因为这个问题中只提供三维场景的图像,而不是三维体积密度的Ground Truth。在3D-GS中,当在随机位置初始化的高斯原语必须在空间中移动才能到达其最终位置时,就会出现局部极小值 。有个两个方法可以阻止这个问题: 1)高斯原语具有局部支持,这意味着如果到正确位置的距离超过几个标准差,梯度就会消失。2)即使一个高斯分布足够接近一个“正确的”位置(局部最优),当接收到梯度时,仍然需要存在一条通往其最终位置的路径,沿着这条路径损失单调地减少 。在可微渲染的上下文中,这通常不是这样的情况,因为高斯经常必须遍历空白空间,在那里它们可能会遮挡背景特征。3D-GS的原文依赖于Adaptive Density Control来解决这种问题。然而,这些技术与泛化性的设置不兼容,在泛化性设置中,原始参数是由一个必须接收梯度的神经网络来预测的。
三、基于图像的三维高斯预测
pixelSplat:给定一对图像及相机参数,可推断出底层场景的三维高斯表示,可以渲染产生看不见的视点的图像。我们的方法包括一个双视图图像编码器(解决尺度模糊性)和一个像素对齐的高斯预测模块。
3.1 双视图图像编码器(解决尺度模糊性)
理想世界中,新视图合成数据集将包含一个度量的相机pose:每个场景Ci m将由一系列元组 C i m C^m _i Cim = {( I j I_j Ij, T j m T^m_j Tjm)}组成。实践中,姿态使用(SfM)计算。SfM只按缩放重建每个场景,这意味着不同的场景Ci是根据单独的、任意比例因子 s i s_i si进行缩放的。因此,给定的场景Ci提供了 C i C_i Ci = {( I j I_j Ij, s i T j m s_iT^m_j siTjm)},其中 s i T j m s_iT^m_j siTjm表示一个度量姿态,其平移分量由未知标量 s i s_i si∈ R + R^+ R+缩放。由于比例模糊性的原则,从单一图像中恢复 s i s_i si是不可能的。在单目深度估计中,这已经通过尺度不变损失[11,13,33]来解决。我们的编码器同样必须预测场景的几何形状,主要是通过每个高斯原语的位置,这取决于每个场景的 s i s_i si.

因此,我们提出了一个双视图编码器来解决尺度模糊性。将两个参考视图表示 为 I I I和 I ~ \tilde{I} I~。对 I I I中的每个像素,将利用 I ~ \tilde{I} I~中对应的外极线,来标注其相应的深度。深度值是根据 I I I和 I ~ \tilde{I} I~的相机pose计算出来的,因此编码了场景的尺度 s i s_i si。然后,我们的编码器通过外极注意[16]找到每个像素的对应关系,并记忆该像素的相应深度。如果在 I ~ \tilde{I} I~中没有对应的像素的深度,则通过每幅图像的自注意来修复的。
具体的:首先通过encoder,将每个视图分别编码为特征 F F F和 F ~ \tilde{F} F~。设u为I的像素坐标,ℓ为其在 I ~ \tilde{I} I~中引入的外极线,即u的相机线在 I ~ \tilde{I} I~ 图像平面上的投影。沿着ℓ,采样像素坐标{ u ~ l \tilde{u}_l u~l}∼ I ~ \tilde{I} I~。对于每个外极线样本{ u ~ l \tilde{u}_l u~l},我们通过u和 u ~ l \tilde{u}_l u~l进一步计算其到 I I I的相机原点的距离 d ~ \tilde{d} d~。然后,我们计算外极性注意的查询、键和值如下:
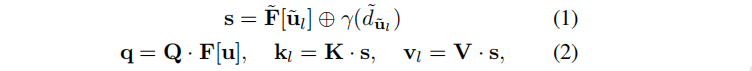
⊕表示拼接,γ(·)表示位置编码,Q、K、V为矩阵。然后执行极性交叉注意,更新逐像素特征F[u]:
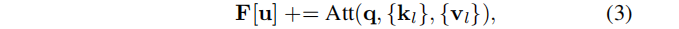
在这个极性注意层之后,每个像素特征F[u]编码了与相机姿态的任意比例因子 s i s_i si一致的尺度深度。
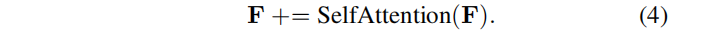
使encoder能够将缩放的深度估计传播到在相反图像中可能没有任何极性对应的部分图像特征图。
3.2 (像素对齐的)高斯参数预测
通过pixel-aligned Gaussians来参数化场景,即:对于每个pixel,将对应的特征作为输入,预测其对应的M个高斯原语。这里为了简单起见,考虑M=1。因此,问题就变为:对于每个像素点,需要预测一个高斯的参数组( µ , Σ , α , S µ, Σ, α, S µ,Σ,α,S)。最重要的问题是,如何参数化每个高斯的位置μ。下图是从scale-aware feature maps中预测pixel-aligned Gaussians的全过程。

首先,如果想预测一个高斯的参数组的话,可以根据pixel特征,直接输入神经网络中挨个预测。尤其是在预测μ时,一个baseline是使用一个神经网络直接预测到从相机远点到高斯均值的距离,如下所示:
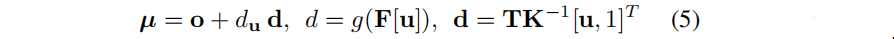
光线方向d通过相机外参T和相机内参K计算。但不幸的是,这种方法容易陷入局部最小值。此外,因为我们需要通过表征进行反向传播,所以就不能利用在3D-GS中提出的生成和剪枝启发式方法,因为它们是不可微的。
因此这篇文章提出:相比于直接预测一个高斯的深度d,我们转而建议预测一个高斯(即表面)在沿射线u的深度d处存在的似然的概率分布。为了实现如此,在一组depth buckets上定义一组离散概率密度。在近平面和远平面之间,将深度分为Z个bins,用一个向量b表示他们,这个b在离散空间上定义,即每个元素 b z b_z bz的定义如下:
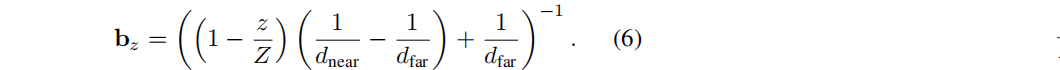
然后,按照索引z,可以定义一个离散概率分布p,它的第z个元素Φ_z表示一个表面存在于第 b z b_z bz 个depth bucket的概率。每个元素Φ都通过该射线出发点u对应的特征F[u]经过一个全连接网络f后来进行预测。此外,还预测了一个per-bucket center offset δ ∈ [0, 1],它可以在bucket边界内调整高斯的深度。
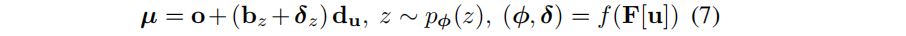
上面这个式子中, d u d_u du是方向。从中可以看出,与直接预测深度不同,这里高斯的位置是从离散分布中采样得到的,而网络需要预测的只是在每个bucket处的概率。
为了训练我们的模型,我们需要将梯度反向传播到depth buckets Φ的概率上。这意味着我们需要计算高斯位置均值μ相对于概率Φ的导数。但是,采样操作 z z z~ p Φ ( z ) p_Φ(z) pΦ(z)操作是不可微分的。所以,作者这里借鉴VAE的思路,采用了重参数化技巧。因此,我们将一个高斯的不透明度设置为与它采样的bucket的概率相等。也就是说,α的值与Φ向量的第z个项目相同。当损失的梯度传递到α时,就可以传递到Φ上。即: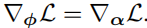
在这种情况,梯度下降增加了高斯分布的不透明度,导致它更高频次的被采样。这最终会将所有的概率质量集中在正确的bucket中,创造出一个完全不透明的表面。考虑一下采样深度不正确的情况。在这种情况下,梯度下降降低了高斯分布的不透明度,降低了进一步错误的深度预测的概率。
除了用神经网络预测概率Φ和偏差δ之外,还需要为每个pixel预测一个协方差矩阵和一组球谐波系数。
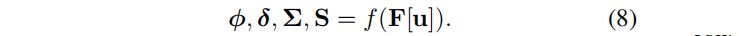
算法流程(使用一个像素的特征来预测一个pixel-aligned Gaussian primitive对应参数的):

四、实验效果
实验设置:
1.RealEstate10k和ACID上训练和评估我们的方法。
2.Baselines: pixelNeRF、GPNR、The unnamed method of 《Learning to render novel views from wide-baseline stereo pairs.》
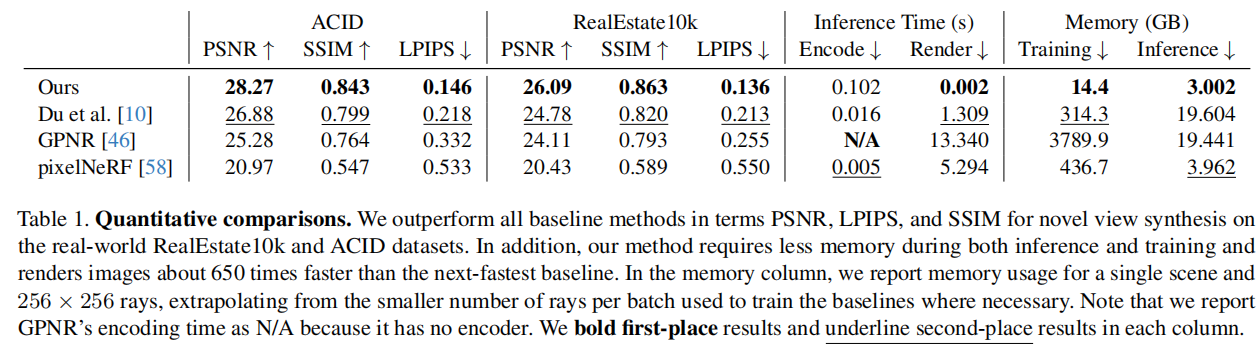


除了质量,在训练和推理花销上,比baseline更少resource-intensive。
为了定性评估推断结构化三维表示的能力,对远远超出训练分布的视图中的高斯进行可视化。下图将点云进行了可视化。虽然pixelSplat 产生的高斯分布在训练分布内的相机姿态上可以实现高保真新视图合成,但它们存在与使用原始3DGS方法优化的三维高斯相同的失效模式。就是,反射平面(reflective surfaces)经常是transparent(透明的),并且,在分布外(out-of-distribution)的视角看时,Gaussians看起来是billboard-like。