学习了王天一博士的机器学习40讲,做个小总结:
1、机器学习中,回归问题隐含了输入变量和输出变量均可连续取值的前提。
2、单变量线性回归,所有样本到直线的欧氏距离之和最小,即均方误差最小化。
3、最小二乘法的几何意义是,计算高维空间上的输出结果在由所有属性共同定义的低维空间上的正交投影。
4、线性回归拟合模型,选择StatsModels这个第三方库,因为它能提供更多的统计意义上的结论,利于更好的理解线性回归模型。
5、在模型拟合前,需要对输入数据做一些处理,比如指标异常值的处理、指标值的归一化等。
6、使用StatsModels模型拟合的步骤包括:
1)首先用add_constant函数,在每个输入数据后面添加一个1,将常数项纳入模型中;——为什么?
2)接着调用OLS,即普通最小二乘法(ordinary least squares),作为拟合对象,计算线性模型的参数;——为什么?
3)然后使用fit函数,获得拟合结果;
4)最后,可以用summary函数打印出拟合模型的统计特性;
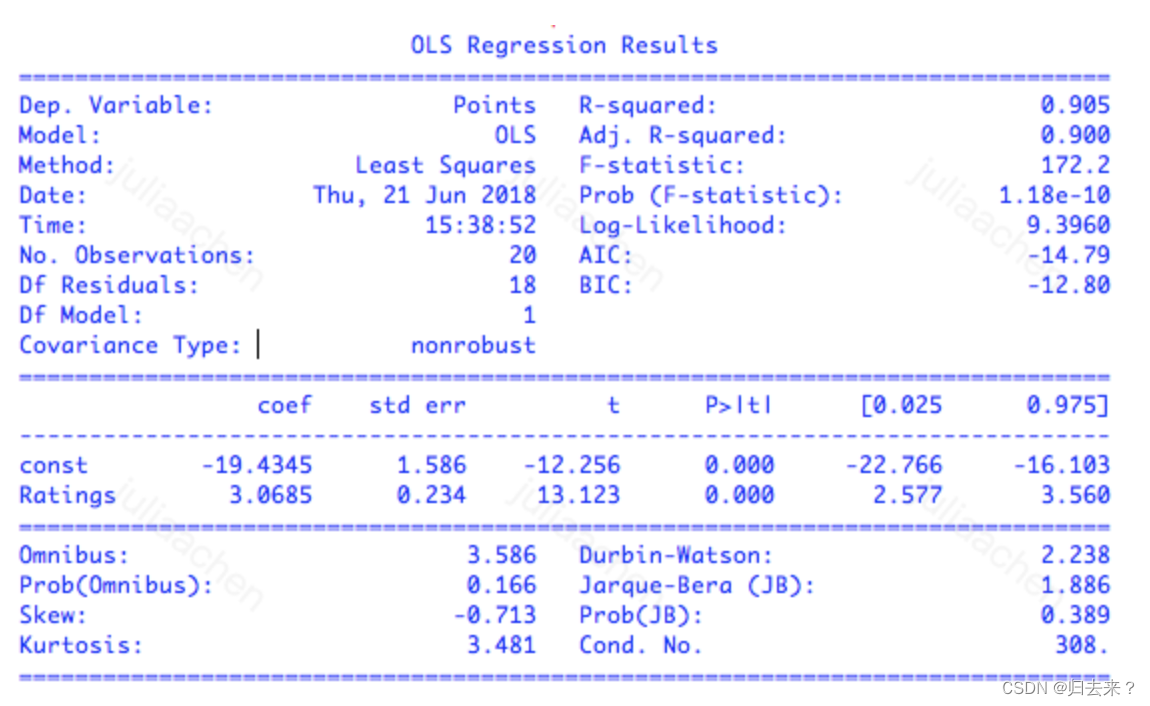
7、模型拟合最核心的结果有,coef表示参数的估计值,也就是通过最小二乘法计算出来的权重系数;
下例中的拟合回归式为:y=3.0685x−19.4345;
std err代表参数估计的标准误差(standard error),表示的是估计值偏离真实值的平均程度;**虽然最小二乘法得到的是无偏估计量,也就是估计结果中不存在系统误差,**但每一个特定的估计值结果依然是在真实值附近波动。——怎么理解标粗的这里?
最后两列[0.025 0.975]给出了 95% 置信区间:每个参数真实值落在这个区间内的可能性是 95%。对于线性回归而言,置信下界和上界分别是估计值减去和加上二倍的标准误,也就是 coef±2×std err。
t和P>|t|是关键指标,评估拟合结果的统计学意义。
t代表t统计量(t-statistic),表示参数估计值与原始假设值之间的偏离程度;它的值越大代表,拟合的结果越可信;在线性回归中通常会假设待拟合的参数值为 0,此时的 t 统计量就等于估计值除以标准误。当数据中的噪声满足正态分布时,t 统计量就满足 t 分布,其绝对值越大意味着参数等于 0 的可能性越小,拟合的结果也就越可信。
P>|t|表示的是P值(p-value),代表当原假设为真时,数据等于观测值或者比观测值更为极端的概率;p值越接近于0,则代表计算出的参数越值得信任;简单地说,p 值表示的是数据与一个给定模型不匹配的程度,p 值越小,说明数据和原假设的模型越不匹配,也就和计算出的模型越匹配。
最上面部分的指标,是对模型拟合数据的程度的评价。
R-squared 表示的是 R2 统计量,也叫作决定系数(coefficient of determination),这个取值在[0, 1]之间的数量表示的是输出的变化中能被输入的变化所解释的部分所占的比例。在这个例子里,R2=0.905 意味着回归模型能够通过 x 的变化解释大约 91% 的 y 的变化,这表明回归模型具有良好的准确性,回归后依然不能解释的 9% 就来源于噪声。
R2统计量具有单调递增的特性,即使在模型中再添加一些和输出无关的属性,计算出来的 R2也不会下降。Adj. R-squared 就是校正版的 R2统计量。当模型中增加的变量没有统计学意义时,多余的不相关属性会使校正决定系数下降。校正决定系数体现出的是正则化的思想,它在数值上小于未校正的 R2统计量。
若是多元线性回归,可能会出现R方和P值矛盾的情况,这时候需要引入F统计量(F-statistic)这个指标,F统计量越大,则模型拟合得越好;F统计量主要应用在多元回归中,它检验的原假设是所有待估计的参数都等于 0,这意味着只要有一个参数不等于 0,原假设就被推翻。F 统计量越大意味着原假设成立的概率越低,理想的 F 值应该在百千量级。
多元线性回归,可能存在由于样本过少导致的过拟合现象,也有可能出现不同属性之间的共线性现象;换句话说,多元线性回归可以有足够的精确性,但对于该精确性的合理解释会比较难,因为在多个属性中,可能有其中多组子属性的组合都能拟合到近似最优的模型效果,但对不同组的子属性的组合解释,会因为属性不同而有很大区别,这就是统计学家莱奥·布雷曼口中的“罗生门”(Rashomon)。
将“罗生门”深挖一步,就是机器学习和统计学在认识论上的差异:统计学讲究的是“知其然,知其所以然”,它不仅要找出数据之间的关联性,还要挖出背后的因果性,给计算出的结果赋予令人信服的解释才是统计的核心。
相比之下,机器学习只看重结果,只要模型能够对未知数据做出精确的预测,那这个模型能不能讲得清楚根本不是事儿。
线性回归学习笔记
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/703800.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
光伏行业该如何起步?
随着全球对可再生能源的需求日益增长,光伏行业作为其中的佼佼者,正迎来前所未有的发展机遇。然而,对于新进入者或希望在这一领域有所建树的企业来说,如何起步并稳健发展是一个值得深思的问题。以下是一些关于光伏行业起步的建议。…
有什么比较方便的裁剪图片软件?7个软件教你轻松裁剪图片
有什么比较方便的裁剪图片软件?7个软件教你轻松裁剪图片
以下是七款比较方便的裁剪图片软件,它们可以帮助您轻松裁剪图片:
图片编辑助手:作为图像处理领域的佼佼者,这款软件提供了多种裁剪工具和功能。您可以使用其…
「Python绘图」绘制同心圆
python 绘制同心圆 一、预期结果 二、核心代码
import turtle
print("开始绘制同心圆")
# 创建Turtle对象
pen turtle.Turtle()
pen.shape("turtle")
# 移动画笔到居中位置
pen.pensize(2) #设置外花边的大小
# 设置填充颜色
pen.fillcolor("green&…
EasyExcel进阶教程
EasyExcel进阶教程 EasyExcel进阶教程概述一、关于表头1.1 多级表头1.2 ExcelProperties注解的index字段和order字段的第一个区别1.3 ExcelProperties注解的index字段和order字段的第二个区别1.4 表头单元格的合并二、动态表头三、样式设置3.1 表头样式设置3.2 数据样式设置Eas…
命令行中,Python 想使用本地环境,但总是显示为Anaconda的虚拟环境
电脑环境
Python 本地环境(Python3.9.5)Anaconda 虚拟环境(Python3.8.8)
遇到的问题
在cmd 中,我想在本地环境使用 Python、pip ,但它却是一直识别成Anaconda的虚拟环境。
解决方法
环境变量配置中&am…
VC++6.0 常用的文件对话框和目录选择对话框
1,文件对话框 //1,弹出文件打开对话框CString strFileName "";char szFilter[] {"exe files(*.exe)|*.exe|All Files(*.*)|*.*|"};CFileDialog dlg(TRUE,NULL,NULL,OFN_HIDEREADONLY | OFN_OVERWRITEPROMPT,szFilter,NULL);if(dlg.DoModal() …
Android中使用Palette让你的页面UI优雅起来
文章目录 1. 什么是Palette2. 引入Palette3. 使用 Palette3.1 同步方式3.2 异步方式3.3 获取色调值 4. 举例4.1 布局文件 activity_palette_list.xml ⬇️4.2 Activity:PaletteListActivity⬇️4.3 列表Adapter:PaletteListAdapter ⬇️4.4 列表item布局…
购买商用ssl证书并在windows服务器IIS上配置https域名(案例为阿里云)
阿里云、华为云等各路云都有ssl证书购买,价格相差不大,操作也都差不多,请自行选择。 本文以阿里云操作为案例。 购买SSL证书
点击购买 付款买入 注意,如果自己搞起来有问题,阿里购买的时候建议选择申请协助服务。购买…
Mysql数据库二进制日志导致磁盘满了处理过程
数据库的二进制日志是数据库管理系统(DBMS)用来记录所有对数据库进行修改的操作的记录。这种日志对于数据库的备份、恢复、复制和审计等操作至关重要。
以MySQL数据库为例,二进制日志(Binary Log)记录了所有更改数据的…
小白必看:新手学编程必会的100个代码
前言
我记得刚开始接触编程的时候,觉得太难了。
也很好奇,写代码的那些人也太厉害了吧?全是英文的,他们的英文水平一定很好吧?
他们是怎么记住这么多代码格式的?而且错了一个标点符号,整个程…
[图解]SysML和EA建模住宅安全系统-03
1 00:00:00,490 --> 00:00:01,180 怎么加
2 00:00:01,570 --> 00:00:04,380 我们来看,这是刚才那个图
3 00:00:05,200 --> 00:00:06,390 17.7
4 00:00:07,150 --> 00:00:08,260 我们同样在这里加
5 00:00:08,430 --> 00:00:10,100 同样在这个下面…







![[图解]SysML和EA建模住宅安全系统-03](https://img-blog.csdnimg.cn/direct/dbdcc9c861b14081a38c87d04ed81874.png)