时序分解 | Matlab实现LMD局域均值分解-编程知识

时序分解 | Matlab实现LMD局域均值分解

效果一览

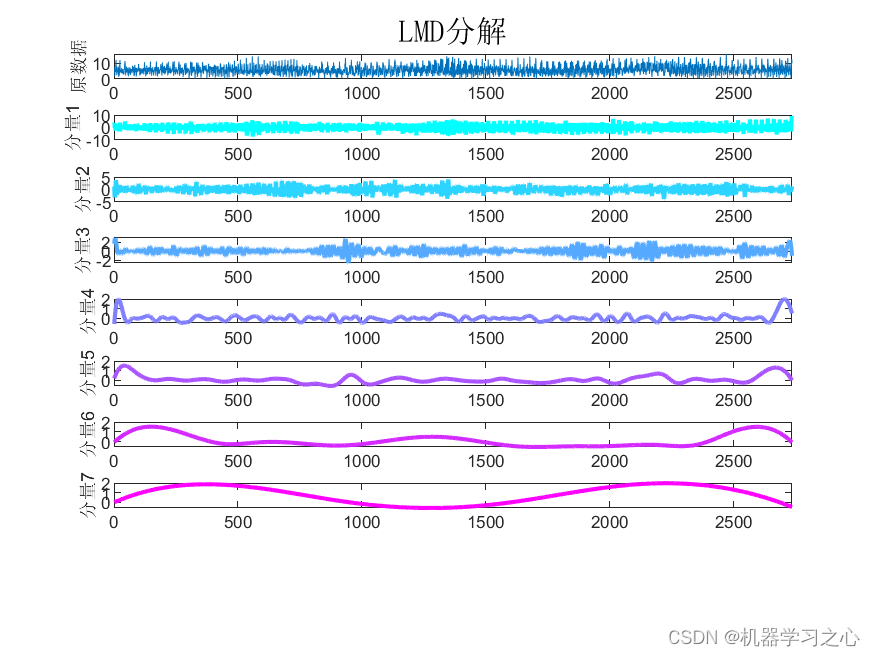
在这里插入图片描述

基本介绍

时序分解 | Matlab实现LMD局域均值分解 Matlab语言
1.算法新颖小众，用的人很少，包含分解图
2.直接替换数据即可用适合新手小白注释清晰～
3.附赠excel测试数据直接运行main一键出图～

局部均值分解算法（LMD）， LMD算法最大的特点就在依据信号本身的特征对信号的自适应分解能力，产生具有真实物理意义的乘积函数（PF）分量（每个PF分量都是一个纯调频信号和包络信号的乘积，且每个PF分量的瞬时频率具有实际物理意义。），并由此得到能够清晰准确反映出信号能量在空间各尺度上分布规律的时频分布，有利于更加细致的对信号特征进行分析。

与此同时，局部均值分解算法（LMD）相较于模态分解的创始算法经验模态分解算法（EMD）而言，其具备端点效应小、迭代次数少等优势。

LMD：不断平滑相邻局部极值点的平均值来获得平均包络函数（局部均值函数）

LMD：不断用原始信号减去局部均值函数并除以包络估计函数（即对其进行解调），并重复直到包络估计函数近似等于1时，得到纯调频信号，在获得纯调频信号后再进行包络信号与纯调频信号相乘得到PF分量。

程序设计

完整源码和数据获取方式资源处下载Matlab实现LMD局域均值分解。

function [PF, residue] = lmd(x)
c = x;
N = length(x);
A = ones(1, N);
PF = [];
aii = 2 * A;while (1)si = c;a = 1;while (1)h = si;maxVec = [];minVec = [];% 寻找最大和最小点for i = 2:N-1if h(i - 1) < h(i) && h(i) > h(i + 1)maxVec = [maxVec i]; 		endif h(i - 1) > h(i) && h(i) < h(i + 1)minVec = [minVec i]; 		endend% 检查是否是残差if (length(maxVec) + length(minVec)) < 2break;end% 处理端点 lenmax = length(maxVec);lenmin = length(minVec);% 左端点if h(1) > 0if maxVec(1) < minVec(1)yleft_max = h(maxVec(1));yleft_min = -h(1);elseyleft_max = h(1);yleft_min = h(minVec(1));endelseif maxVec(1) < minVec(1)yleft_max = h(maxVec(1));yleft_min = h(1);elseyleft_max = -h(1);yleft_min = h(minVec(1));endend% 右端点if h(N) > 0if maxVec(lenmax) < minVec(lenmin)yright_max = h(N);yright_min = h(minVec(lenmin));elseyright_max = h(maxVec(lenmax));yright_min = -h(N);endelseif maxVec(lenmax) < minVec(lenmin)yright_max = -h(N);yright_min = h(minVec(lenmin));elseyright_max = h(maxVec(lenmax));yright_min = h(N);endend% 获取maxVec和minVec的包络，使用spline插值maxEnv = spline([1 maxVec N], [yleft_max h(maxVec) yright_max], 1:N);minEnv = spline([1 minVec N], [yleft_min h(minVec) yright_min], 1:N);mm = (maxEnv + minEnv) / 2;aa = abs(maxEnv - minEnv) / 2;mmm = mm;aaa = aa;preh = h;h = h - mmm;si = h ./ aaa;a = a .* aaa;    aii = aaa;B = length(aii);C = ones(1, B);bb = norm(aii - C);if (bb < 1000)break;endendpf = a .* si;PF = [PF; pf];bbb = length(maxVec) + length(minVec);% 检查是否是残差if (length(maxVec) + length(minVec)) < 5break;endc = c - pf;end