目录

一，3146. 两个字符串的排列差

二，3147. 从魔法师身上吸取的最大能量

三，3148. 矩阵中的最大得分

四，3149. 找出分数最低的排列

---

一，3146. 两个字符串的排列差

本题就是求同一个字符在两个字符串中的下标之差的绝对值的和，可以使用数组来统计字符的下标，再求下标之差的绝对值的和。

代码如下：

class Solution {public int findPermutationDifference(String s, String t) {int[] cnt = new int[26];int idx = 0;for(char ch : s.toCharArray()){cnt[ch-'a'] = idx++; }idx = 0;int ans = 0;for(char ch : t.toCharArray()){ans += Math.abs(cnt[ch-'a']-idx++);}return ans;}
}

二，3147. 从魔法师身上吸取的最大能量

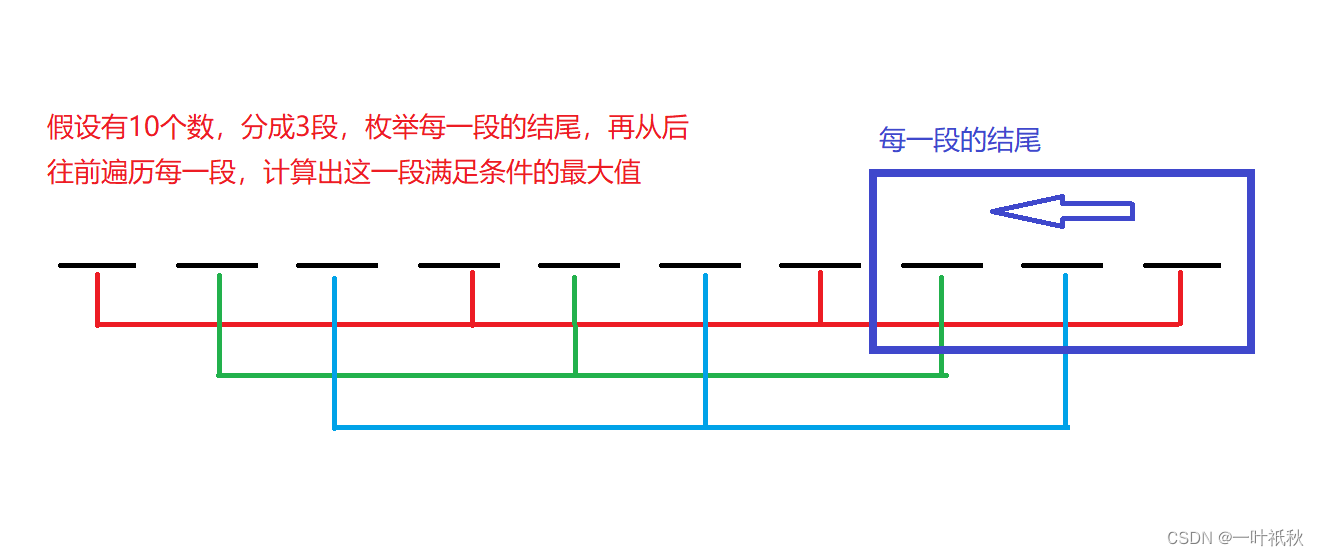
本题实际上就是把energy数组分成k段，求每一段中连续子数组的最大值（开始位置随便，结束位置必须是这一段的结尾），所以可以枚举每一段的结束位置，倒着往前遍历，求最大值，有点像希尔排序。画个图理解一下：

代码如下：

class Solution {public int maximumEnergy(int[] energy, int k) {int n = energy.length;int ans = Integer.MIN_VALUE;for(int i=n-1; i>=n-k; i--){int res = 0;for(int j=i; j>=0; j-=k){res += energy[j];ans = Math.max(res, ans);}}return ans;}
}

三，3148. 矩阵中的最大得分

写本题前有一点要注意到：A -> B -> C 的得分和 A -> C 的得分是一样的，也就是说，只需要关注起点和终点的差就行，即只需要找到NxM的矩阵中的子矩形它的 终点 - 起点 最大就行。

所以这题就有点类似于求二维前缀和，只不过这里是求二维最小值f[i][j]，而答案就是 g[i][j] - Math.min( f[i-1][j]，f[i][j-1])，中的最大值

注意：题目要求必须移动一次，所以不能使用 g[i][j] - f[i][j] 来求最大值，可能出现原地不动的情况

class Solution {//f[i+1][j+1]:表示(0,0)->(i,j)这个矩阵的最小值public int maxScore(List<List<Integer>> grid) {int n = grid.size(), m = grid.get(0).size();int[][] f = new int[n+1][m+1];for(int i=0; i<n+1; i++) f[i][0] = Integer.MAX_VALUE;for(int j=0; j<m+1; j++) f[0][j] = Integer.MAX_VALUE;int ans = Integer.MIN_VALUE;for(int i=0; i<n; i++){for(int j=0; j<m; j++){f[i+1][j+1] = Math.min(f[i+1][j], f[i][j+1]);ans = Math.max(ans, grid.get(i).get(j) - f[i+1][j+1]);f[i+1][j+1] = Math.min(f[i+1][j+1], grid.get(i).get(j));}}return ans;}
}

四，3149. 找出分数最低的排列

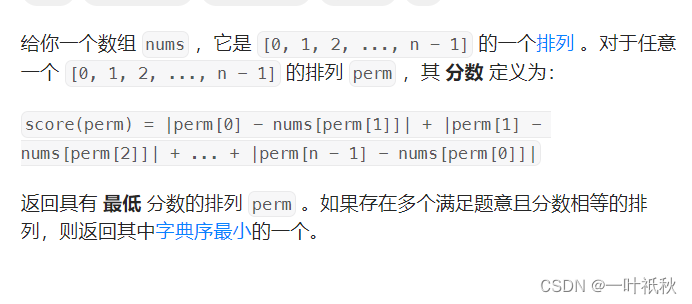
按照暴力的思路来看，枚举[0，.....，n]的所有排列顺序，（之前使用过的后面就不能再次使用），计算出其中分数最低且字典序最小的排序。所以使用 dfs 需要两个参数，一个是之前已使用过的数（这是无序的，只有相邻的数才会对分数产生影响），二是当前位置的前一个数（这是为了计算它的分数）。

• dfs(i，j)：表示在选择过 i 集合（使用二进制来表示集合）中的数，且前一个数为 j 的最低的分数。
• 从小到大枚举下一个可以选择的数 k，res = Math.max( res, dfs(i|1<<k, k) + Math.abs( k - nums[k]) )
• 当所有的数都选过之后，直接 return Math.abs(j - nums[0])

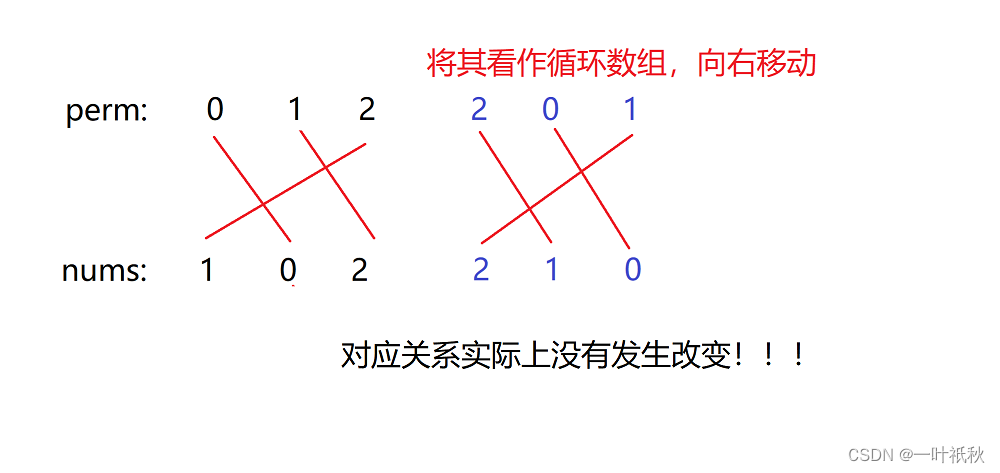
起始位置一定可以等于 0：实际上这里只要 perm[i] 与 nums[perm[i+1]] 的对应关系不变，起始位置可以是任何数，只不过题目要求字典序最小，所以这里起始位置为 0。画个图理解一下：

另外一点，题目不是要求返回最小值，而是要返回perm数组，所以还需要多写一步，获取perm数组的方法直接看代码注释。

代码如下：

class Solution {int[] nums;int n;int[][] memo;public int[] findPermutation(int[] nums) {this.n = nums.length;this.nums = nums;memo = new int[1<<14][14];for(int[] row : memo)Arrays.fill(row, -1);int[] ans = new int[n];print_dfs(1, 0, ans, 0);//1：表示集合中有0return ans;}int dfs(int i, int j){if(i == (1<<n)-1){return Math.abs(j-nums[0]);}if(memo[i][j]!=-1) return memo[i][j];int res = Integer.MAX_VALUE;for(int x=1; x<n; x++){//枚举可取的数if((i>>x&1)==0)//该数没有被选择过res = Math.min(res, dfs(i|1<<x, x) + Math.abs(j - nums[x]));}return memo[i][j] = res;}void print_dfs(int i, int j, int[] ans, int idx){ans[idx] = j;//记录数组if(i == (1<<n)-1){return;}int final_ans = dfs(i, j);//找到(i,j)最小的值for(int x=1; x<n; x++){//从小到大遍历，确保字典序最小if((i>>x&1)==1)continue;if(final_ans == dfs(1<<x|i, x) + Math.abs(j-nums[x])){//如果值相同，说明当前数选择的就是xprint_dfs(i|1<<x, x, ans, idx+1);break;}}}
}