【智能算法】清道夫优化算法（CFO）原理及实现-编程知识

【智能算法】清道夫优化算法（CFO）原理及实现

1.背景

2024年，W Zhang受到清道夫自然行为启发，提出了清道夫优化算法（Cleaner Fish Optimization Algorithm, CFO）。

在这里插入图片描述

2.算法原理

2.1算法思想

CFO模拟了清道夫在进行“清洁服务”时的移动行为，以及雌鱼变性为雄鱼的行为，并定义了两种位置更新模式。此外，还提出了一种两代循环操作策略来实现优化过程。

在这里插入图片描述

2.2算法过程

CFO采用三次混沌映射对算法进行初始化，保持了算法的多样性，提高了算法的全局搜索能力:
$\begin{aligned}&r_{k+1,j}=4r_{k,j}^3-3r_{k,j},\quad-1<r_{1,j}<1,\quad r_{k,j}\neq0\\&k=1,2,...,N-1.\quad j=1,2,...,d\end{aligned}\tag{1}$

种群初始化：
$X_{i,j}=lb_{i,j}+(ub_{i,j}-lb_{i,j})\cdot\left(\frac{r_{i,j}+1}2\right)\tag{2}$

CFO 提出了两代循环策略：分别是目标追踪和性别转换。一代采用目标追踪更新模式以实现“清洁服务”。而在下一代中，前三分之二的个体采用目标追踪更新模式，其他个体采用性别转换更新模式。

目标追踪

清道夫目标追踪行为:
$X_{i,j}^{t+1}=X_{i,j}^t+V_{i,j}^t\tag{2}$
清道夫速度:
$V_{i,j}^{t+1}=V_{i,j}^t+(X_{i,j}^t-X_{best,j})\cdot f\tag{3}$
f为每个个体对应的频率:
$f=f_{min}+(f_{max}-f_{min})\cdot r_1\tag{4}$
其中fmin, fmax分别为最小和最大频率。它们分别被设置为0和10。为了增强算法的探索能力，引入了随机行走策略:
$X_{i,j}=\begin{cases}X_{best,j}+0.1\cdot rand\cdot\alpha^{t},&if\quad r_{2}<r\\X_{i,j}^{t},&otherwise&&\end{cases}\tag{5}$
参数表述为:
$\alpha^{t+1}=0.97\times\alpha^t\tag{6}$
$\alpha$ 表示清道夫的清洁能力，也表示随着迭代次数的增加，清道夫的清洁能力下降。r为自适应参数:
$r=1-e^{-\gamma\cdot t}\tag{7}$

性别转换

在鱼类群体中，当雄性死亡时，雌性可能会改变性别，成为新的雄性。基于这种行为，本文提出了性别转换更新模式：
$X_{i,j}^{t+1}=w\cdot X_{i,j}^t+r_3\cdot(X_{i,j}^t-X_{best,j})\tag{8}$
w为自适应权值，用于平衡探索和开发:
$w=(w_{max}-w_{min})^{e^{\frac tT}}+w_{min}\tag{9}$

鱼类种群行为

清道夫是群居动物，为了表现这种行为，引入了准反射反向学习策略：
$X_{i,j}=r_{4}\times\left(X_{i,j}^{t}-\frac{ub_{i,j}+lb_{i,j}}{2}\right)-\frac{ub_{i,j}+lb_{i,j}}{2}\tag{10}$

流程图

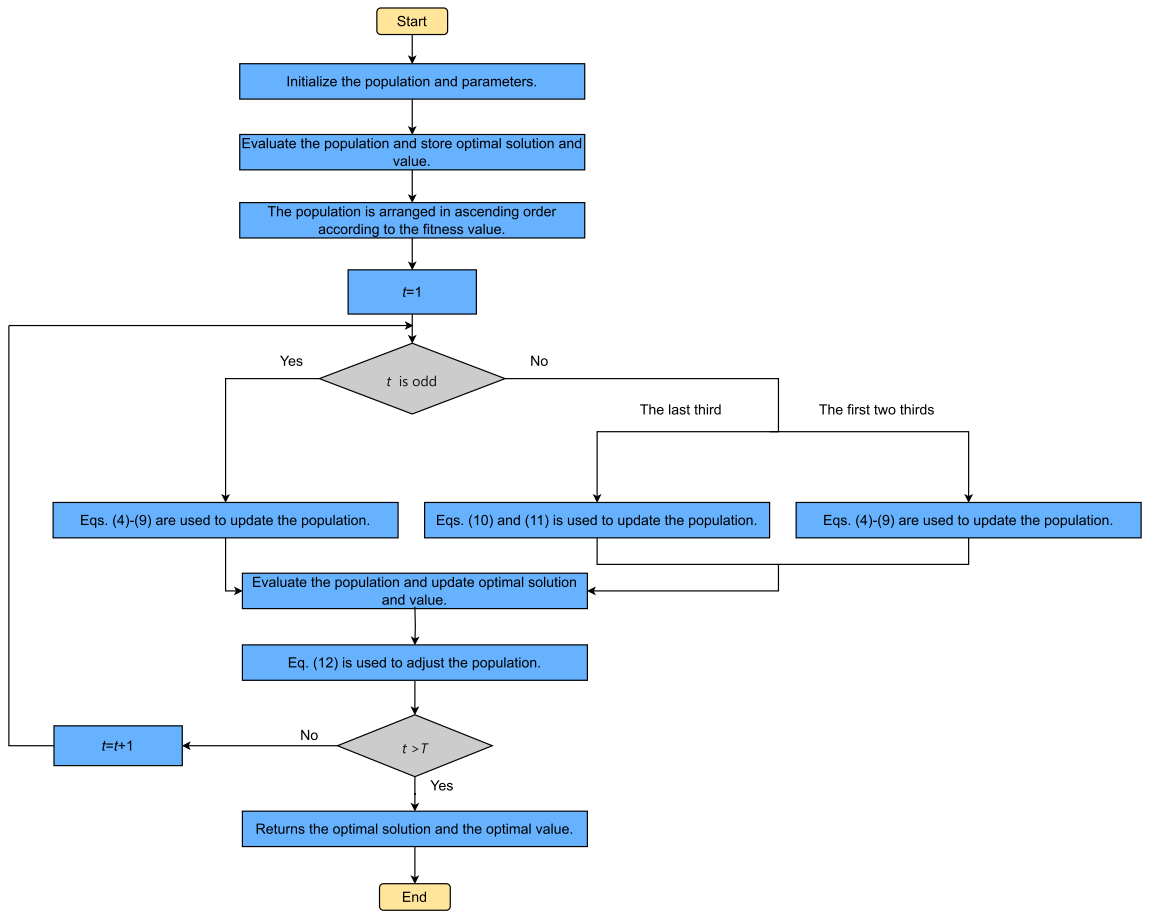
在这里插入图片描述

伪代码

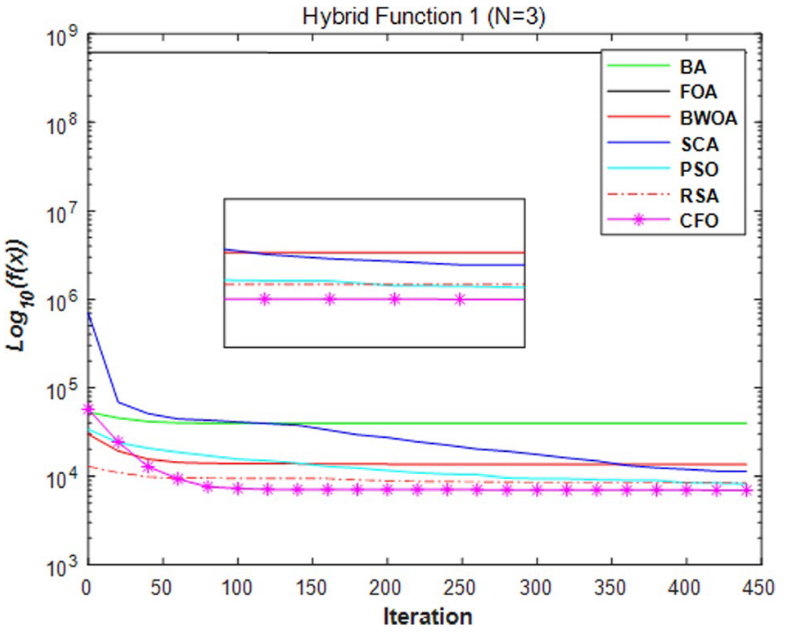
在这里插入图片描述

3.结果展示

在这里插入图片描述

4.参考文献

[1] Zhang W, Zhao J, Liu H, et al. Cleaner fish optimization algorithm: a new bio-inspired meta-heuristic optimization algorithm[J]. The Journal of Supercomputing, 2024: 1-39.