【c++】map和set的封装

1.红黑树源码

我们使用上节课的红黑树源码来封装map和set.
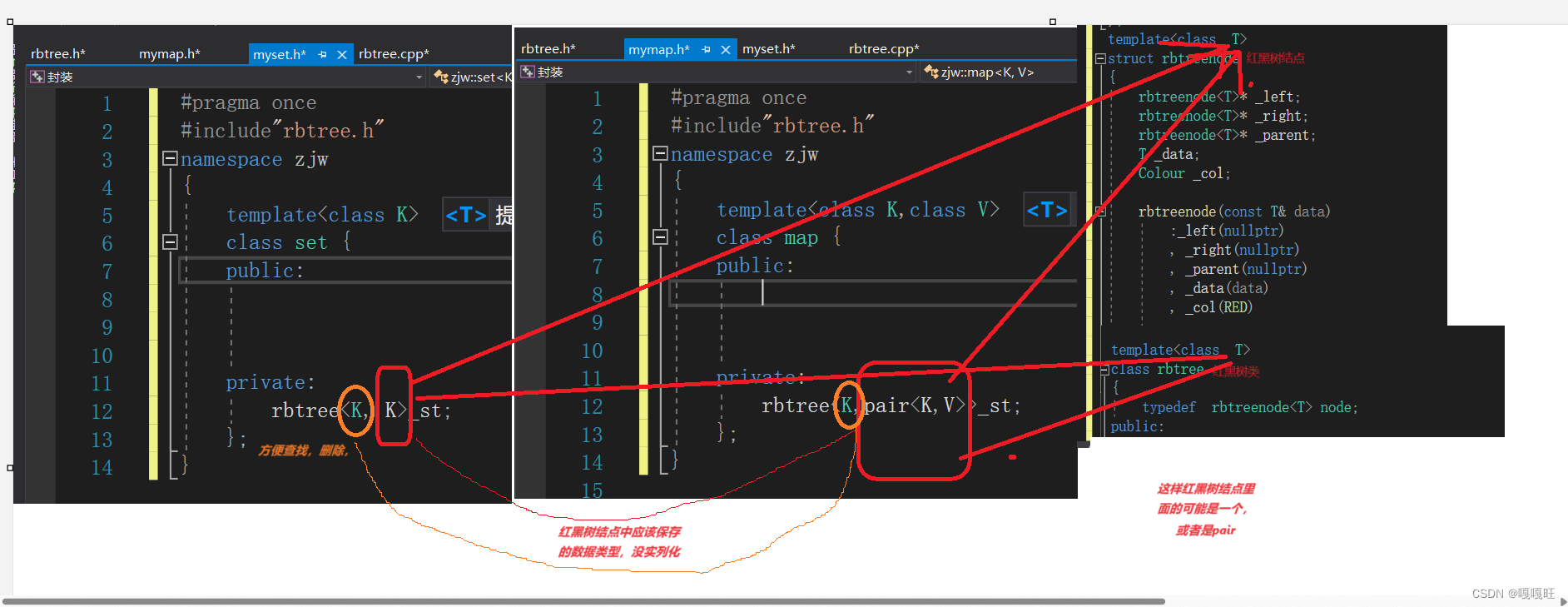
因为map存的是（key,value）,set存的是（key）,为了我们set和map使用同一个类模板（红黑树），所以我们先要修改红黑树结点中存的数据类型，我们使用模板来初始化，根据实列化来决定结点中存的是pair,还是只有一个数据

做出修改：代码中所有key的地方用data代替，而data的数据类型是T，当是set实列化的时候T就是int(一种)，当是map的时候T就是pair,比方说pair<string,int>

#include<iostream>
#include<string>
using namespace std;
enum Colour
{RED,BLACK};
template<class  T>
struct rbtreenode
{rbtreenode<T>* _left;rbtreenode<T>* _right;rbtreenode<T>* _parent;T _data;Colour _col;rbtreenode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}};template<class  T>
class rbtree
{typedef  rbtreenode<T> node;
public:void spinleft(node* parent){node* subr = parent->_right;node* subrl = subr->_left;parent->_right = subrl;if (subrl)subrl->_parent = parent;subr->_left = parent;node* ppnode = parent->_parent;parent->_parent = subr;if (ppnode == nullptr){_root = subr;subr->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subr;subr->_parent = ppnode;}else{ppnode->_right = subr;subr->_parent = ppnode;}}}void spinright(node* parent){node* subl = parent->_left;node* sublr = subl->_right;parent->_left = sublr;if (sublr)sublr->_parent = parent;subl->_right = parent;node* ppnode = parent->_parent;parent->_parent = subl;if (ppnode == nullptr){_root = subl;subl->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subl;subl->_parent = ppnode;}else{ppnode->_right = subl;subl->_parent = ppnode;}}}void spinlr(node* parent){node* subl = parent->_left;node* sublr = subl->_right;//int bf = sublr->_bf;spinleft(parent->_left);spinright(parent);/*	if (bf == 1){subl->_bf = -1;sublr->_bf = 0;parent->_bf = 0;}else if (bf == -1){subl->_bf = 0;sublr->_bf = 0;parent->_bf = 1;}else{subl->_bf = 0;sublr->_bf = 0;parent->_bf = 0;}*/}void spinrl(node* parent){node* subr = parent->_right;node* subrl = subr->_left;//int bf = subrl->_bf;spinright(subr);spinleft(parent);/*	if (bf == 1){parent->_bf = -1;subr->_bf = 0;subrl->_bf = 0;}else if (bf == -1){parent->_bf = 0;subr->_bf = 1;subrl->_bf = 0;}else{subr->_bf = 0;subrl->_bf = 0;parent->_bf = 0;}*/}bool insert(const T& data){if (_root == nullptr){_root = new node(data);_root->_col = BLACK;return true;}node* cur = _root;node* parent = nullptr;while (cur){if (cur->_data > data){parent = cur;cur = cur->_left;}else if (cur->_data < data){parent = cur;cur = cur->_right;}else{return false;}}cur = new node(data);if (parent->_data > data){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){node* grandfather = parent->_parent;if (parent == grandfather->_left){node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){spinright(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{spinleft(parent);spinright(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){spinleft(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{spinright(parent);spinleft(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}bool Check(node* cur){if (cur == nullptr)return true;if (cur->_col == RED && cur->_parent->_col == RED){cout << cur->_key<< "存在连续的红色节点" << endl;return false;}return Check(cur->_left)&& Check(cur->_right);}bool IsBalance(){if (_root && _root->_col == RED)return false;return Check(_root);}void inorder(){_inorder(_root);}void _inorder(node* root){if (root == nullptr)return;_inorder(root->_left);cout << root->_data  << endl;_inorder(root->_right);}node* Find(const T& data){node* cur = _root;node* parent = nullptr;while (cur){if (cur->_data > data){parent = cur;cur = cur->_left;}else if (cur->_data < _data){parent = cur;cur = cur->_right;}else{return cur;}}return nullptr;}private:int treeheight(node* root){if (root == nullptr)return 0;int leftheight = treeheight(root->_left);int rightheight = treeheight(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;}node* _root = nullptr;};
int main()
{rbtree<int>st;int a[] = //{ 16,3,1 };//测试右旋//{ 16,32,58 };//测试左旋//{ 8,3,1,10,6,4};//测试右左旋{ 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };for (auto e : a){st.insert(e);}st.inorder();int ret = st.IsBalance();cout << endl;cout << ret;}

2.set和map类的简单封装

在这里插入图片描述

#pragma once
#include"rbtree.h"
namespace zjw
{template<class K,class V>class map {public:private:rbtree<K,pair<K,V>>_st;};
}
#pragma once
#include"rbtree.h"
namespace zjw
{template<class K>class set {public:private:rbtree<K, K>_st;};
}

3.map和set调用底层rbtree的insert函数

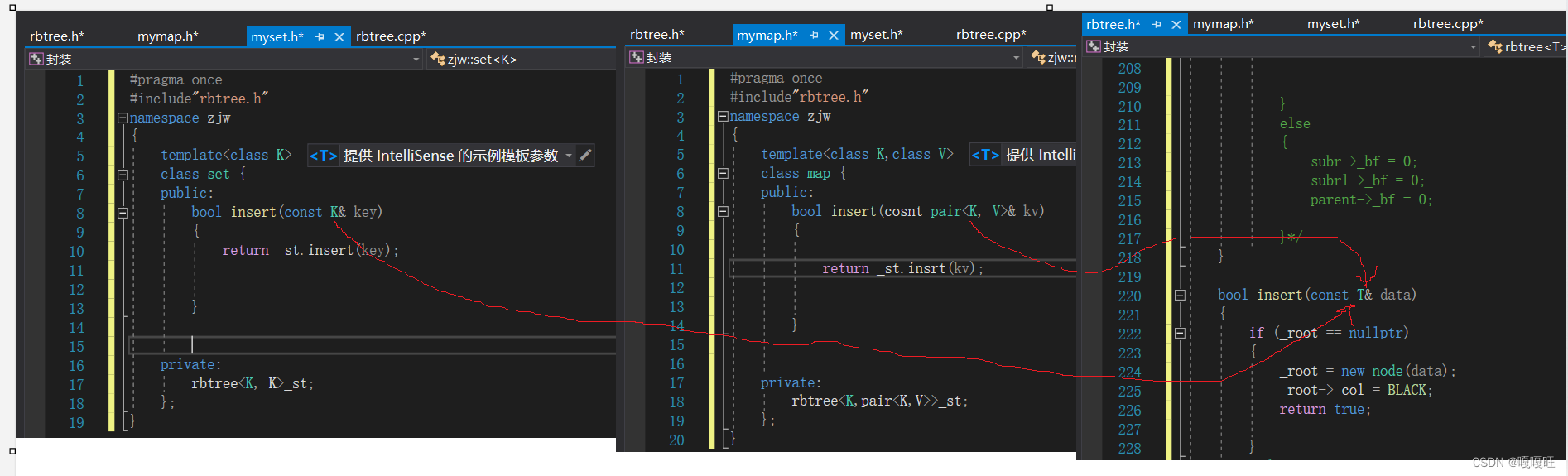
在这里插入图片描述

#pragma once
#include"rbtree.h"
namespace zjw
{template<class K,class V>class map {public:bool insert(cosnt pair<K, V>& kv){return _st.insrt(kv);}private:rbtree<K,pair<K,V>>_st;};
}
#pragma once
#include"rbtree.h"
namespace zjw
{template<class K>class set {public:bool insert(const K& key){return _st.insert(key);}private:rbtree<K, K>_st;};
}

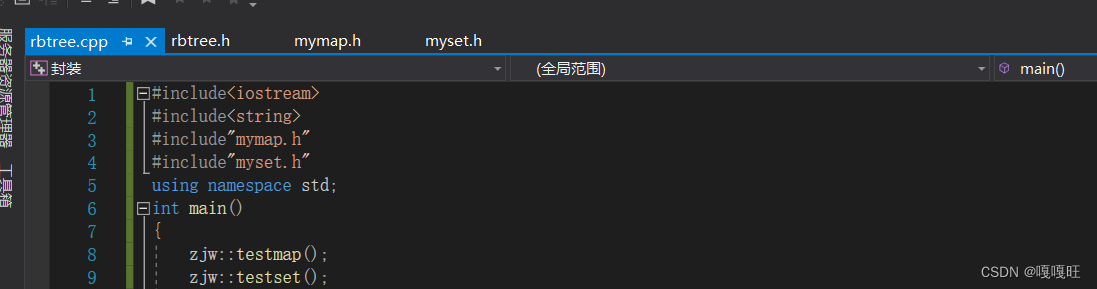
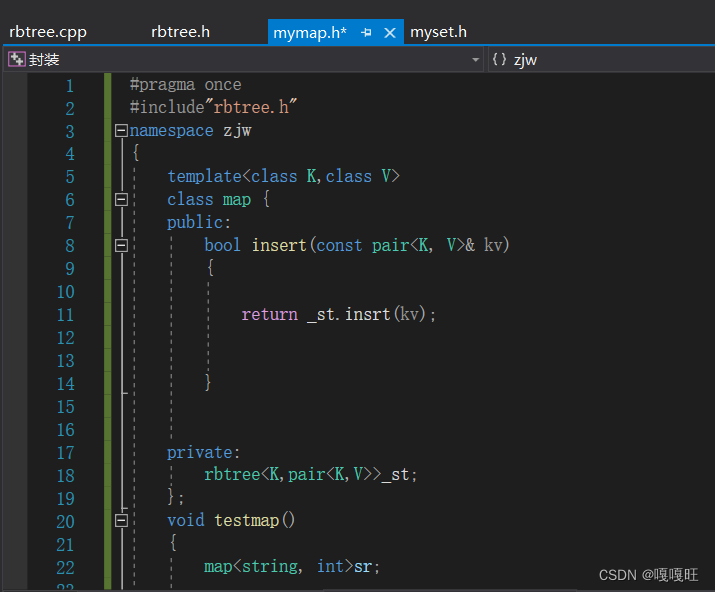
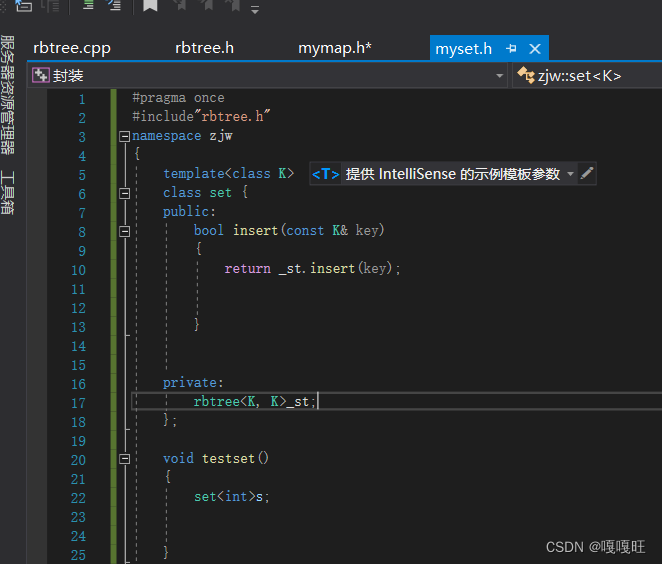
4.阶段测试

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

5._data的元素提取

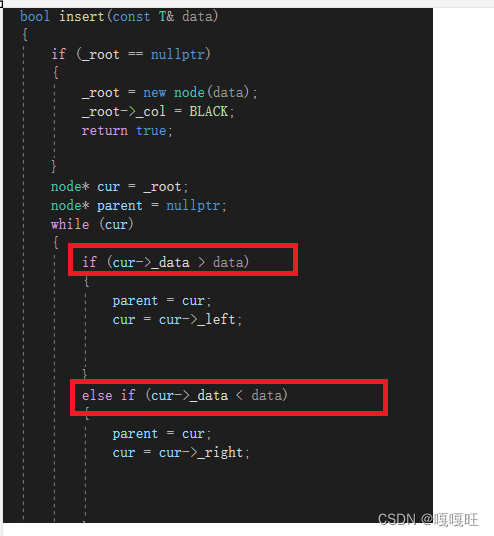
因为我们不管是map还是set,他们插入都是根据第一个模板参数比较大小，来确定插入当前结点的左还是右，但是为什么之前的代码没有报错？？
因为如果是map的话，pair也是可以比较大小的，规则是第一个大的大。第一个一样大，就比较第二个，第二个谁大就大
在这里插入图片描述
但是我们回顾之前的map和set都是按照第一个比较，所以我们可以这样做。在map和set类中定义内部类，如果rbtree中有需要比较data大小时，初始化一个内部类取data第一个内容来比较，我们只需要在map和set中初始化一个内部类对象即可返回data的第一个内容。
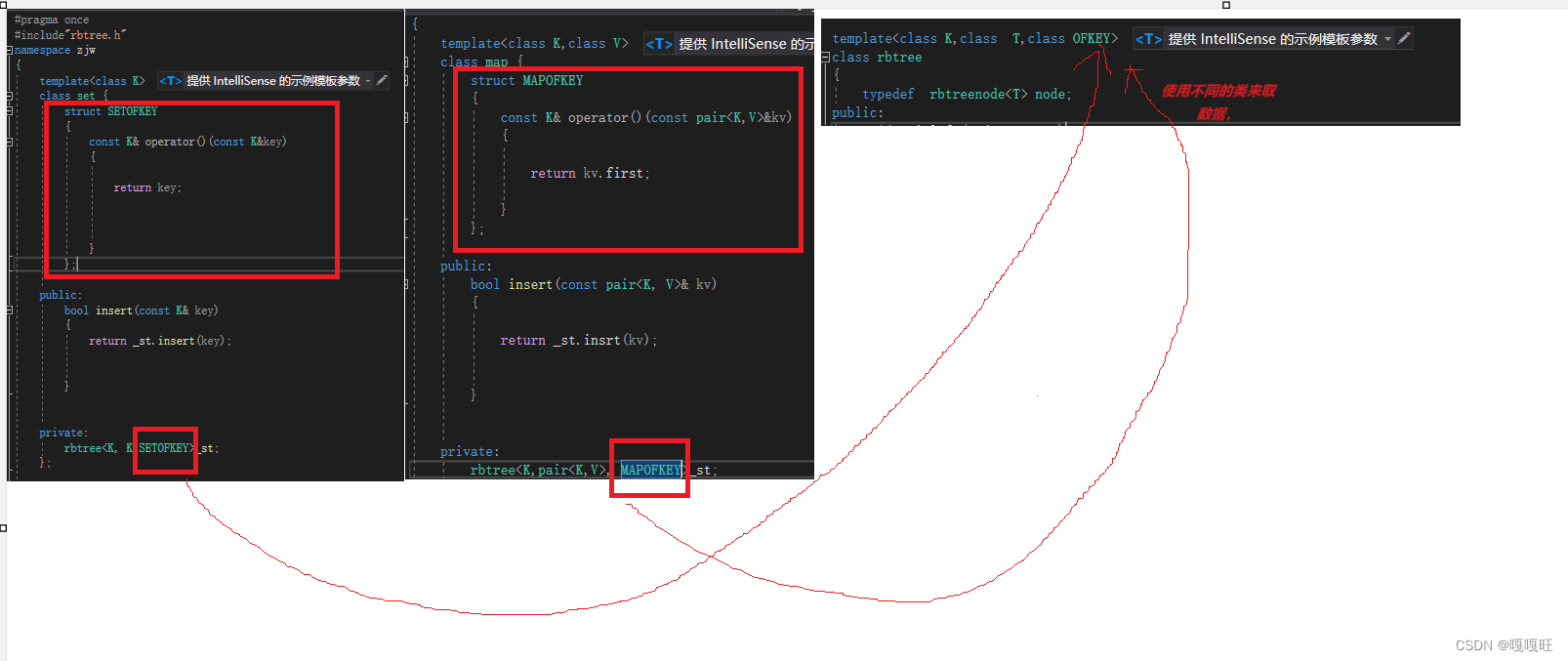
在这里插入图片描述

在rbtree中需要比较_data的地方都需要使用类对象来返回data的第一个内容

#pragma once
#include<iostream>
#include<string>
using namespace std;
enum Colour
{RED,BLACK};
template<class  T>
struct rbtreenode
{rbtreenode<T>* _left;rbtreenode<T>* _right;rbtreenode<T>* _parent;T _data;Colour _col;rbtreenode(const T& data):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _col(RED){}};template<class K,class  T,class OFKEY>
class rbtree
{typedef  rbtreenode<T> node;
public:void spinleft(node* parent){node* subr = parent->_right;node* subrl = subr->_left;parent->_right = subrl;if (subrl)subrl->_parent = parent;subr->_left = parent;node* ppnode = parent->_parent;parent->_parent = subr;if (ppnode == nullptr){_root = subr;subr->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subr;subr->_parent = ppnode;}else{ppnode->_right = subr;subr->_parent = ppnode;}}}void spinright(node* parent){node* subl = parent->_left;node* sublr = subl->_right;parent->_left = sublr;if (sublr)sublr->_parent = parent;subl->_right = parent;node* ppnode = parent->_parent;parent->_parent = subl;if (ppnode == nullptr){_root = subl;subl->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subl;subl->_parent = ppnode;}else{ppnode->_right = subl;subl->_parent = ppnode;}}}void spinlr(node* parent){node* subl = parent->_left;node* sublr = subl->_right;//int bf = sublr->_bf;spinleft(parent->_left);spinright(parent);/*	if (bf == 1){subl->_bf = -1;sublr->_bf = 0;parent->_bf = 0;}else if (bf == -1){subl->_bf = 0;sublr->_bf = 0;parent->_bf = 1;}else{subl->_bf = 0;sublr->_bf = 0;parent->_bf = 0;}*/}void spinrl(node* parent){node* subr = parent->_right;node* subrl = subr->_left;//int bf = subrl->_bf;spinright(subr);spinleft(parent);/*	if (bf == 1){parent->_bf = -1;subr->_bf = 0;subrl->_bf = 0;}else if (bf == -1){parent->_bf = 0;subr->_bf = 1;subrl->_bf = 0;}else{subr->_bf = 0;subrl->_bf = 0;parent->_bf = 0;}*/}bool insert(const T& data){OFKEY sk;if (_root == nullptr){_root = new node(data);_root->_col = BLACK;return true;}node* cur = _root;node* parent = nullptr;while (cur){if (sk(cur->_data) > sk(data)){parent = cur;cur = cur->_left;}else if (sk(cur->_data) < sk(data)){parent = cur;cur = cur->_right;}else{return false;}}cur = new node(data);if (sk(parent->_data) > sk(data)){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_col == RED){node* grandfather = parent->_parent;if (parent == grandfather->_left){node* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){spinright(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{spinleft(parent);spinright(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else{node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = BLACK;uncle->_col = BLACK;grandfather->_col = RED;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_left){spinleft(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{spinright(parent);spinleft(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}bool Check(node* cur){if (cur == nullptr)return true;if (cur->_col == RED && cur->_parent->_col == RED){cout << cur->_data << "存在连续的红色节点" << endl;return false;}return Check(cur->_left)&& Check(cur->_right);}bool IsBalance(){if (_root && _root->_col == RED)return false;return Check(_root);}void inorder(){_inorder(_root);}void _inorder(node* root){if (root == nullptr)return;_inorder(root->_left);cout << root->_data << endl;_inorder(root->_right);}node* Find(const T& data){OFKEY sk;node* cur = _root;node* parent = nullptr;while (cur){if (sk(cur->_data) > sk(data)){parent = cur;cur = cur->_left;}else if (sk(cur->_data) < sk(data)){parent = cur;cur = cur->_right;}else{return cur;}}return nullptr;}private:int treeheight(node* root){if (root == nullptr)return 0;int leftheight = treeheight(root->_left);int rightheight = treeheight(root->_right);return leftheight > rightheight ? leftheight + 1 : rightheight + 1;}node* _root = nullptr;};

6.迭代器

template<class T,class Pef,class Ptr>
struct _rbtreeIterator
{typedef rbtreenode<T> node;typedef _rbtreeIterator<T, Pef, Ptr> Self;Node* _node;
public:_rbtreeIterator(Node* node):_node(node){//默认构造}Self& operator++(){//迭代器++}Self& operator--(){//迭代器--}bool operator!=(Self& s){//两个结点是否是同一结点}Pef operator*(){//重载*}Ptr operator->(){//重载->}};

上面迭代器封装在list里面有说过

template<class T,class Pef,class Ptr>
struct _rbtreeIterator
{typedef rbtreenode<T> node;typedef _rbtreeIterator<T, Pef, Ptr> Self;Node* _node;
public:_rbtreeIterator(Node* node):_node(node){//默认构造}Self& operator++(){//迭代器++}Self& operator--(){//迭代器--}bool operator!=(Self& s){//两个结点是否是同一结点return _node != s._node;}Pef operator*(){//重载*return _node->_data;}Ptr operator->(){//重载->return &_node->_data}};

重点说一下迭代器++和–，
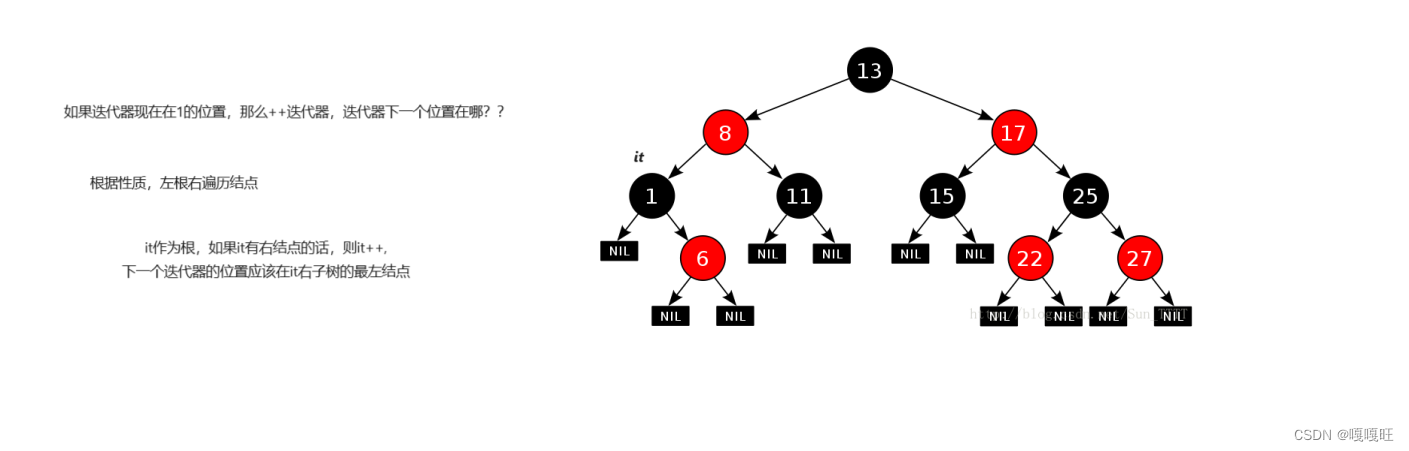
在这里插入图片描述

	Self& operator++(){//迭代器++if (_node->_right){Node* next = _node->_right;while (next->_left){next = next->_left;}_node = next;}}

如果_node没有右结点的话，迭代器++下一个位置应该是哪里呢？
比方说_node在6的位置
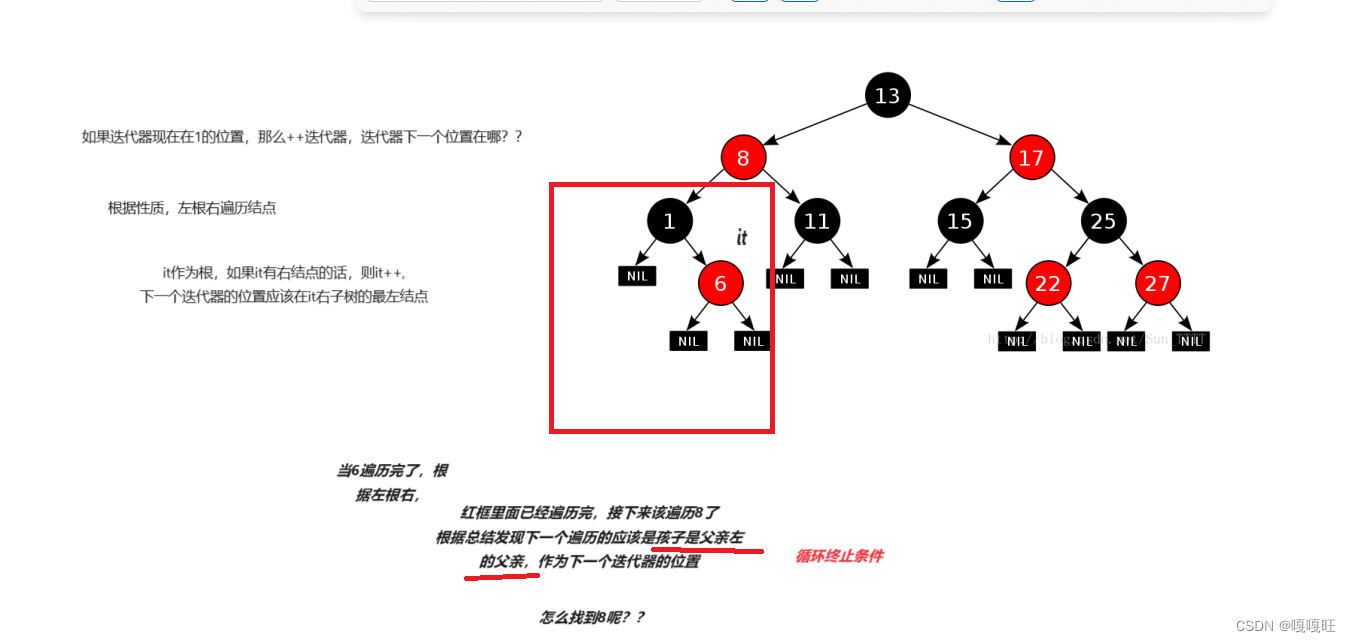
在这里插入图片描述

	Self& operator++(){//迭代器++if (_node->_right){Node* next = _node->_right;while (next->_left){next = next->_left;}_node = next;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_right)//循环找孩子是父亲左的父亲，该父亲是下一个迭代器的结点{cur = parent;parent = parent->_parent;}_node = parent;}return *this;}

同理–

	Self& operator--(){//迭代器--if (_node->_left){Node* next = _node->_left;while (next->_right){next = next->_right;}_node = next;}else{Node* cur = _node;Node* parent = cur->_parent;while (parent && cur == parent->_left){cur = parent;parent = parent->_parent;}_node = parent;}return *this;}

红黑树调用迭代器


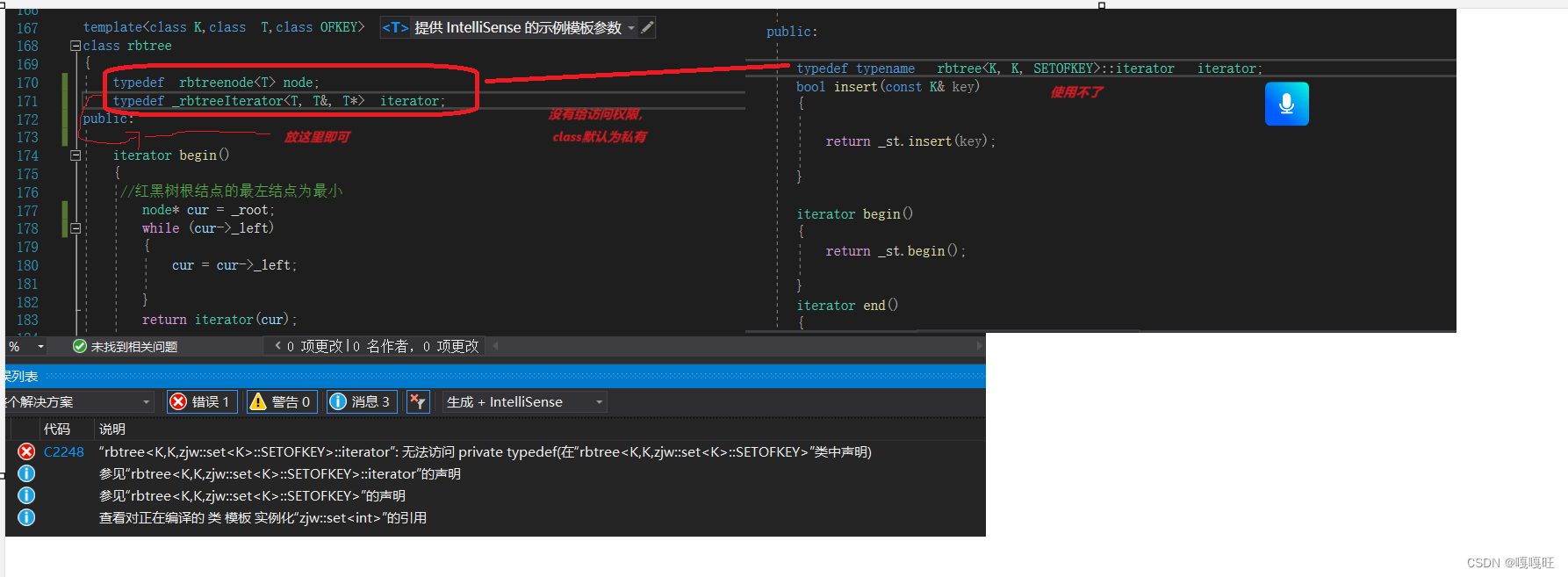
template<class K,class  T,class OFKEY>
class rbtree
{typedef  rbtreenode<T> node;typedef _rbtreeIterator<T, T&, T*>  iterator;
public:iterator begin(){//红黑树根结点的最左结点为最小node* cur = _root->_left;while (cur){cur = cur->_left;}return iterator(cur);}iterator end(){//空return iterator(nullptr);}

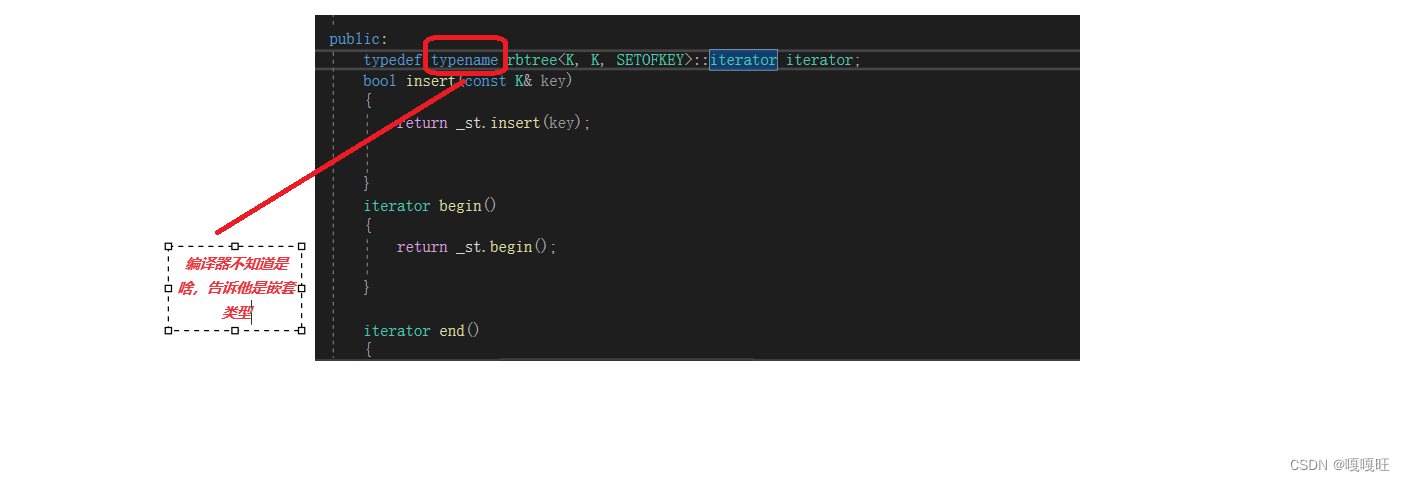
在这里插入图片描述
在这里插入图片描述

7.set迭代器测试

#pragma once
#include"rbtree.h"
namespace zjw
{template<class K>class set {struct SETOFKEY{const K& operator()(const K&key){return key;}};public:typedef typename rbtree<K, K, SETOFKEY>::iterator iterator;bool insert(const K& key){return _st.insert(key);}iterator begin(){return _st.begin();}iterator end(){return _st.end();}private:rbtree<K, K,SETOFKEY>_st;};void testset(){set<int>s;int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16,14 };for (auto e : a){s.insert(e);}set<int>::iterator it = s.begin();while (it != s.end()){cout << *it << endl;++it;}}}

#include<iostream>
#include<string>
#include"mymap.h"
#include"myset.h"
using namespace std;
int main()
{//zjw::testmap();zjw::testset();}

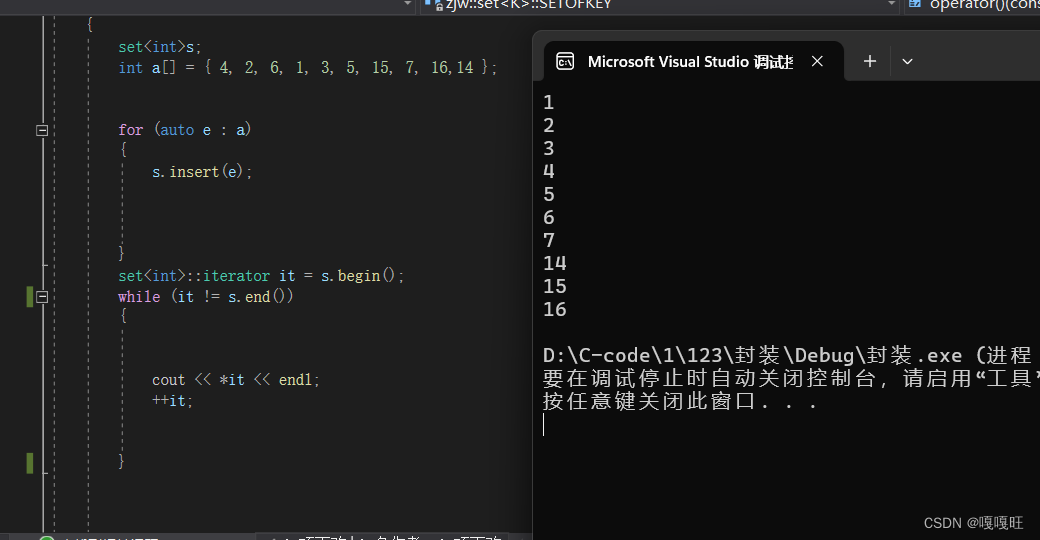
在这里插入图片描述

8.map迭代器测试

#pragma once
#include"rbtree.h"
namespace zjw
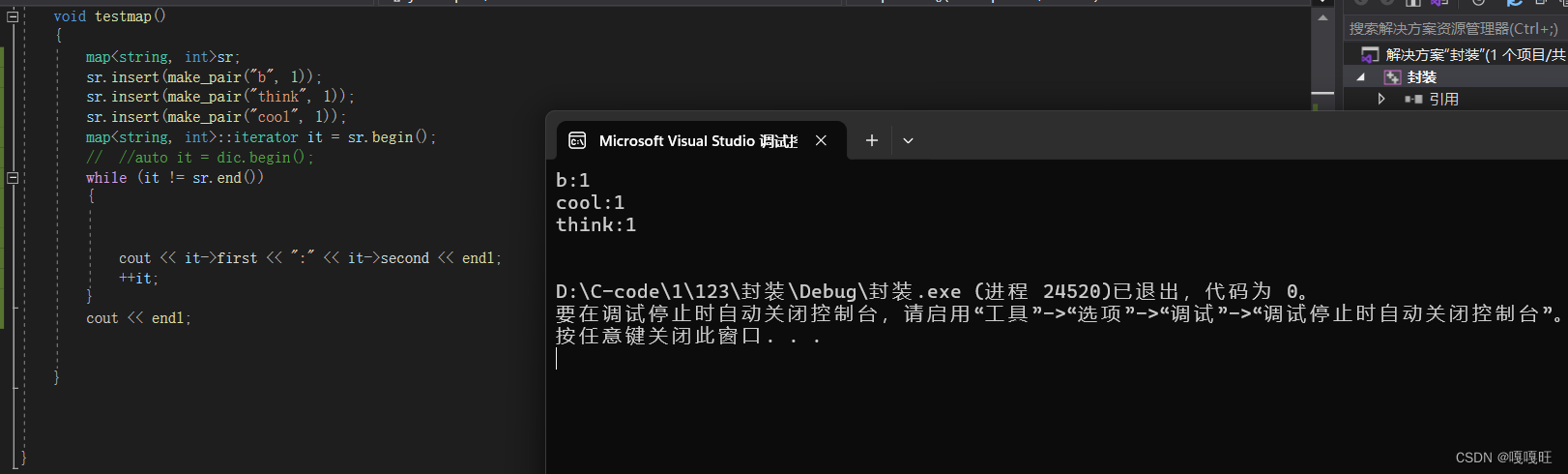
{template<class K,class V>class map {struct MAPOFKEY{const K& operator()(const pair<K,V>&kv){ return kv.first;}};public:typedef typename rbtree<K, pair<K,V>, MAPOFKEY>::iterator iterator;bool insert(const pair<K, V>& kv){return _st.insert(kv);}iterator begin(){return _st.begin();}iterator end(){return _st.end();}private:rbtree<K,pair<K,V>, MAPOFKEY>_st;};void testmap(){map<string, int>sr;sr.insert(make_pair("b", 1));sr.insert(make_pair("think", 1));sr.insert(make_pair("cool", 1));map<string, int>::iterator it = sr.begin();//	//auto it = dic.begin();while (it != sr.end()){cout << it->first << ":" << it->second << endl;++it;}cout << endl;}}

#include<iostream>
#include<string>
#include"mymap.h"
#include"myset.h"
using namespace std;
int main()
{zjw::testmap();//zjw::testset();}

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/706313.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

51单片机入门：I2C通讯协议

51单片机入门：I2C通讯协议

I2C通讯协议 I2C简介 串口通信只能在两个设备之间进行&#xff0c;如果是三个设备相互通讯&#xff0c;那么每个设备需要两组串口&#xff0c;实际上是3组相互独立的串口通信。如果是4个设备相互通信就更加麻烦了&#xff0c;最突出的问题就是线路连接比较复杂。 为了解决这个…
阅读更多...
迈向数字化生产：MES系统的重要性与功能解析

迈向数字化生产：MES系统的重要性与功能解析

在传统的加工生产企业中&#xff0c;流程卡一直是进行生产跟踪控制的主要工具。流程卡上印刷了工序列表&#xff0c;每个工序都需要作业人员打勾、签名并标注日期&#xff0c;以确保产品在生产线上经过所有必要的工序。 然而&#xff0c;随着信息技术的发展&#xff0c;制造业也…
阅读更多...
【漏洞复现】泛微OA E-Cology GetLabelByModule SQL注入漏洞

【漏洞复现】泛微OA E-Cology GetLabelByModule SQL注入漏洞

漏洞描述&#xff1a; 泛微OA E-Cology是一款面向中大型组织的数字化办公产品&#xff0c;它基于全新的设计理念和管理思想&#xff0c;旨在为中大型组织创建一个全新的高效协同办公环境。泛微OA E-Cology getLabelByModule存在SQL注入漏洞&#xff0c;允许攻击者非法访问和操…
阅读更多...
linux系统查看CPU信息

linux系统查看CPU信息

1、查看cpu型号 [rootMaster ~]# cat /proc/cpuinfo | grep name | cut -f2 -d: | uniq -c 40。Intel(R) Xeon(R) CPU E5-2650 v3 2.30GHz 2、查看系统中实际物理CPU的颗数&#xff08;物理&#xff09; [rootMaster ~]# grep physical id /proc/cpuinfo | sort | uniq | w…
阅读更多...
第 8 章 机器人底盘Arduino端PID控制(自学二刷笔记)

第 8 章 机器人底盘Arduino端PID控制(自学二刷笔记)

重要参考&#xff1a; 课程链接:https://www.bilibili.com/video/BV1Ci4y1L7ZZ 讲义链接:Introduction Autolabor-ROS机器人入门课程《ROS理论与实践》零基础教程 8.4.5 底盘实现_04Arduino端PID控制 上一节最后测试时&#xff0c;电机可能会出现抖动、顿挫的现象&#xff…
阅读更多...
Java：【反射】、【枚举】、【lambda表达式】

Java：【反射】、【枚举】、【lambda表达式】

一、【反射】的定义 Java的反射机制&#xff1a; 是在【运行状态】中&#xff0c;对于任意一个类&#xff0c;能够知道这个类的【所有属性和方法】&#xff1b;对于任何一个对象&#xff0c;能够调用它的【任意方法和属性】&#xff1b;这种【动态获取信息】以及【动态调用对…
阅读更多...
玩转Matlab-Simscape（初级）- 07 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真（理论部分3）

玩转Matlab-Simscape（初级）- 07 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真（理论部分3）

** 玩转Matlab-Simscape&#xff08;初级&#xff09;- 07 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真&#xff08;理论部分3&#xff09; ** 目录 玩转Matlab-Simscape&#xff08;初级&#xff09;- 07 - 基于Solidworks、Matlab Simulink、COMSOL的协同仿真&am…
阅读更多...
酷开科技丨女性群像大戏《惜花芷》在酷开系统热播中

酷开科技丨女性群像大戏《惜花芷》在酷开系统热播中

在这个国产剧市场蓬勃发展的时代&#xff0c;酷开科技通过其生态智能电视系统&#xff0c;为剧迷们打造了一个精彩的观剧平台。通过酷开科技的智能推荐算法&#xff0c;消费者能够轻松地发掘并观看各种题材的高质量剧集&#xff0c;无论是扣人心弦的金融较量、深刻的家庭代际关…
阅读更多...
编程实战：自己编写HTTP服务器（系列5：执行后台shell命令）

编程实战：自己编写HTTP服务器（系列5：执行后台shell命令）

初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github&#xff1a;codetoys&#xff0c;所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C的&#xff0c;可以在任何平台上使用。 系列入口&#xff1a;编程实战…
阅读更多...
【文档理解】TextMonkey：一种OCR-Free的用于文档理解的多模态大模型

【文档理解】TextMonkey：一种OCR-Free的用于文档理解的多模态大模型

背景 传统的信息提取&#xff0c;通常是从文本中提取信息&#xff0c;相关技术也比较成熟。然而对于复杂领域&#xff0c;例如图片&#xff0c;文档等形式的数据&#xff0c;想要提取出高质量的、可信的数据难度就比较大了&#xff0c;这种任务也常称为&#xff1a;视觉文档理…
阅读更多...
职业生涯第一课---“Redis分布式锁优化：确保唯一性与效率“

职业生涯第一课---“Redis分布式锁优化：确保唯一性与效率“

前言 最近因为刚入职公司开启自己的实习生涯&#xff0c;工作和毕设论文同步进行&#xff0c;导致有段时间没更新博客了&#xff0c;今天来分享一下最近学到的一些知识。 场景介绍 BOSS让我写一些接口&#xff0c;他提出这样一个需求&#xff0c;该接口的参数有多个&#xf…
阅读更多...
Windows下配置TortoiseGit 访问Ubuntu虚拟机下Samba共享目录

Windows下配置TortoiseGit 访问Ubuntu虚拟机下Samba共享目录

前言&#xff1a; 本文记录学习使用 Git 版本管理工具的学习笔记&#xff0c;通过阅读参考链接中的博文和实际操作&#xff0c;快速的上手使用 Git 工具。 本文参考了引用链接博文里的内容。 引用: 【TortoiseGit】TortoiseGit安装和配置详细说明-CSDN博客 Git版本管理可视…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023