题目描述

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意： 答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

提示：

• 3 <= nums.length <= 3000
• -10^5 <= nums[i] <= 10^5

解题思路一：

将原始数组进行从小到大进行排序，然后定义三个指针a,b,c，初始时分别指向数组的第一个元素、第二个元素、第三个元素，并且b所指位置永远在a之后，c所指元素永远在b之后，表示正在尝试的三元组，然后定义三层循环，分别表示遍历移动这三个元素，如果三个值相加为0，则添加进结果列表。如果向后移动的元素与前一个元素值相同，则直接跳过，因为已经试过了，减少遍历次数的同时也避免了重复三元组的出现。直到a遍历到了数组的倒数第二个位置，结束。

实现的代码

class Solution {public List<List<Integer>> threeSum(int[] nums) {Arrays.sort(nums);List<List<Integer>> result = new ArrayList<>();int i,j,k,len=nums.length,a,b,c;for(i=0;i<len-2;i++){if(i==0||nums[i]!=nums[i-1]){// 当前遍历的值前面没有遍历过，则进入第二层循环a = nums[i];for(j=i+1;j<len-1;j++){if(j==i+1||nums[j]!=nums[j-1]){// 当前遍历的值前面没有遍历过，则进入第三层循环b = nums[j];for(k=j+1;k<len;k++){if(k==j+1||nums[k]!=nums[k-1]){// 当前遍历的值前面没有遍历过，则进行计算是否符合条件c = nums[k];if(a+b+c==0){//符合三元组条件List<Integer> l = new ArrayList<>();l.add(a);l.add(b);l.add(c);result.add(l);}}}}}}}return result;}
}

结果：过了308个测例，但还是超出时间限制，时间复杂度过高，分析代码逻辑可知，时间复杂度为O(n^3)

解题思路二：

由前面的思路以及之前做的题可知，HashMap的检索时间复杂度为O(1)，所以当确定了前两个元素值之后，第三个元素值只能等于0-(a+b)，因此可以利用HashMap直接检索是否存在0-(a+b)，时间复杂度将为O(n^2)。所以先遍历一次数组，构建HashMap，其中的键是数组元素值，值为该数组元素在数组中的次数。每次遍历某个元素后将map中对应的值-1，表示已经使用了一个该元素。

代码：

class Solution {public List<List<Integer>> threeSum(int[] nums) {Arrays.sort(nums);List<List<Integer>> result = new ArrayList<>();Map<Integer,Integer> mapValues = new HashMap<>();Map<Integer,Integer> mapIndex = new HashMap<>();// 用于存储每个元素第一次出现在数组中的位置，int i,j,k,len=nums.length,a,b,c;for(i=0;i<len;i++){if(i==0||nums[i]!=nums[i-1]){// 该元素之前没出现过，则将其新加入map,mapValues.put(nums[i],1);}else{// 该元素已经出现过，将对应键值对的值+1mapValues.put(nums[i],mapValues.get(nums[i])+1);}mapIndex.put(nums[i],i);//更新位置map添加位置信息}for(i=0;i<len-2;i++){if(i==0||nums[i]!=nums[i-1]){// 当前遍历的值前面没有遍历过，则进入第二层循环a = nums[i];mapValues.put(a,mapValues.get(a)-1); //表示该元素已经使用一个for(j=i+1;j<len-1;j++){if(j==i+1||nums[j]!=nums[j-1]){// 当前遍历的值前面没有遍历过，则进行三元组计算b = nums[j];mapValues.put(b,mapValues.get(b)-1); //表示该元素已经使用一个c = 0-a-b;if(mapValues.containsKey(c) && mapIndex.get(c)>j && mapValues.get(c)>0){// 还存在三元组所需要的c,且c的位置是在b之后List<Integer> l = new ArrayList<>();l.add(a);l.add(b);l.add(c);result.add(l);}mapValues.put(b,mapValues.get(b)+1); //表示该元素已经使用一个}}mapValues.put(a,mapValues.get(a)+1); //恢复成原个数}}return result;}
}

结果：

不过时间消耗和空间消耗都非常大，还有很大改进空间。

解题思路3：

通过分析内层循环可知，当固定了a之后，那么b和c只能从a之后的位置去找，同时如果一开始固定b为a的后一个元素，c是最后一个元素，那么当a+b+c<0时，说明b+c的值不够，又因为c已经是最大的值了，只可能移动b来增大b+c的值。同理，当a+b+c>0时，说明b+c的值超过了，又因为b已经是最小的值了，只可能移动c来减小b+c的值。因此内层的b和c循环实际上是并列的关系，可以通过一次遍历来判断。

改进之后代码：

class Solution {public List<List<Integer>> threeSum(int[] nums) {Arrays.sort(nums);List<List<Integer>> result = new ArrayList<>();int i,j,k;for(i=0;i<nums.length-2;i++){if(i>0&&nums[i]==nums[i-1]){continue;}j = i+1;// 初始化j为i的后一位k = nums.length-1;// 初始化k为数组最后一个数while(j<k){// 当j处于k的左边则进一步判断int sum = nums[i]+nums[j]+nums[k];if(sum>0){k--;}else if(sum<0){j++;}else{// 满足三元组要求List<Integer> l = new ArrayList<>();l.add(nums[i]);l.add(nums[j]);l.add(nums[k]);result.add(l);// j继续向右移动，k继续向左移，寻找是否j++;k--;while(j<k&&nums[j]==nums[j-1])j++ ;// 向后移动的b与当前三元组的b值一样，不需要重复计算while(j<k&&nums[k]==nums[k+1])k--; // 向前移动的c与当前三元组的c值一样，不需要重复计算}}}return result;}
}

结果：

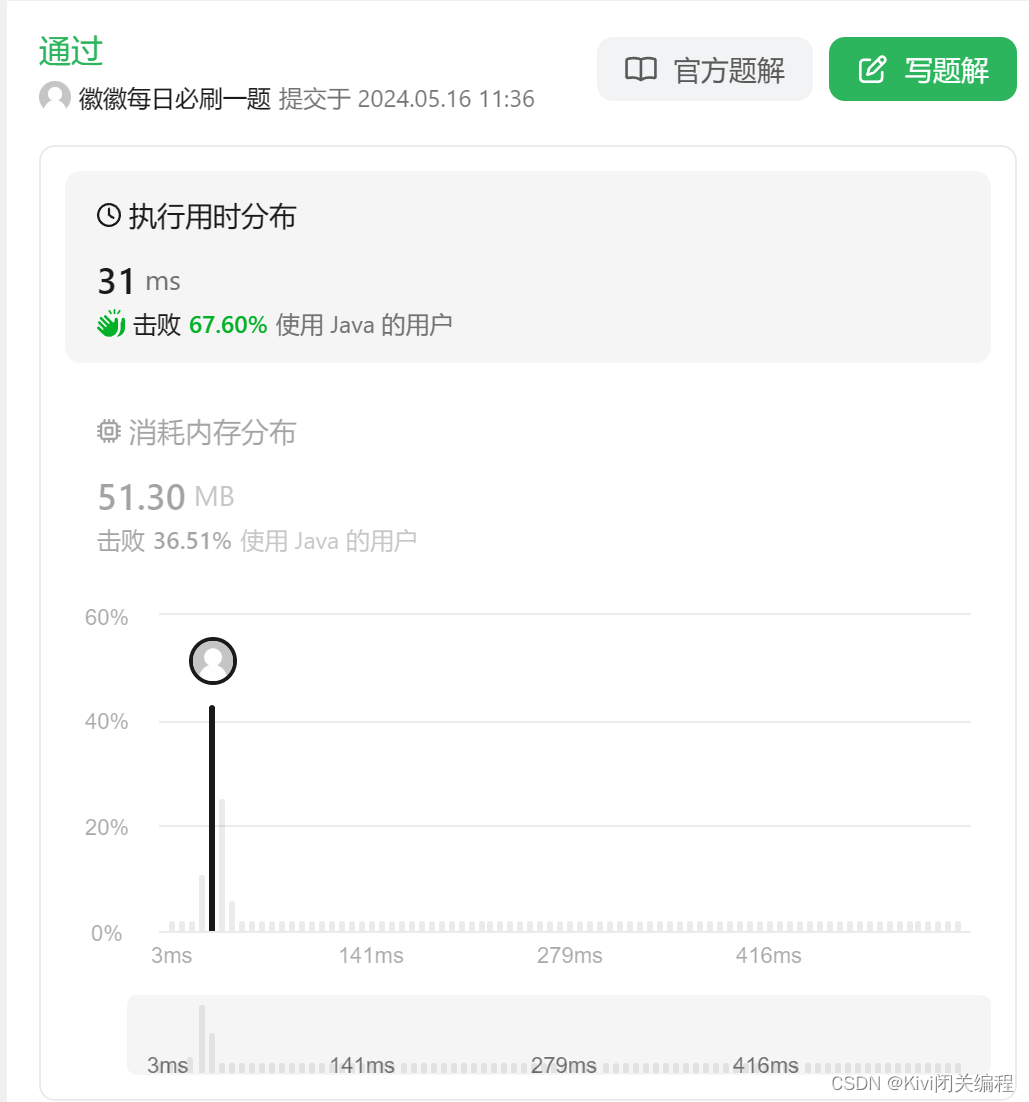
总结：
需要通过两个数去寻找他们和的固定值，可以通过排序+双指针问题去解决。不断通过判断离固定值的差距去调整双指针的位置。