算法day08-编程知识

算法day08

第一题

1. 两数之和

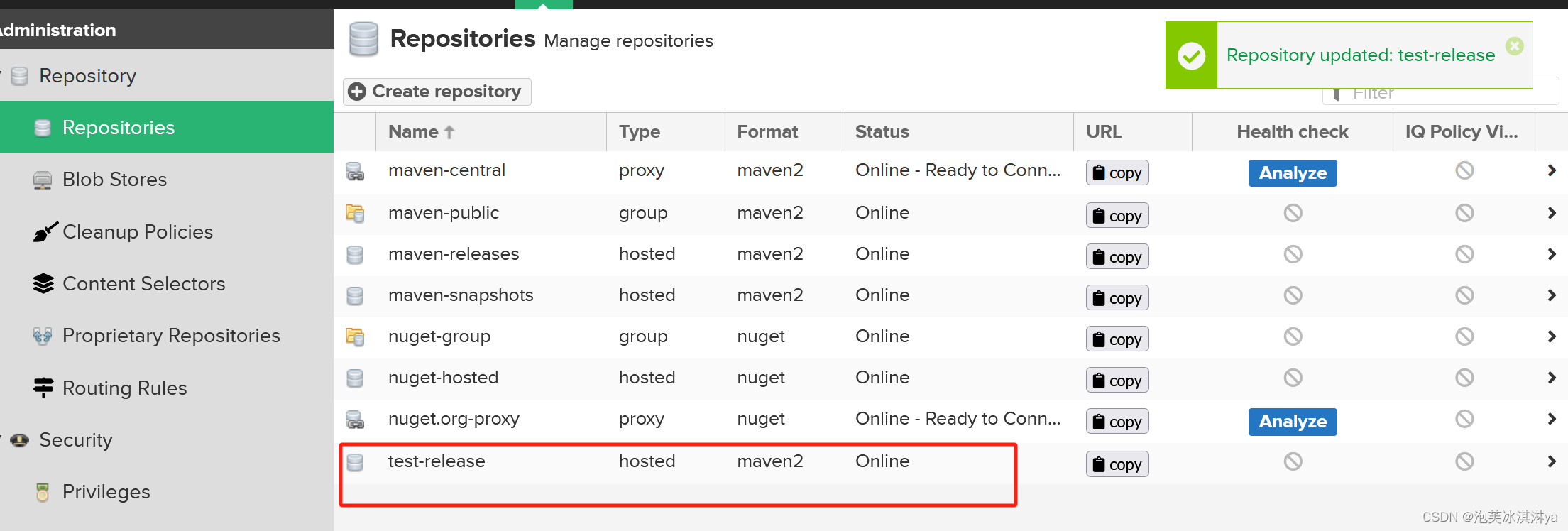
由上述题意所知，本题要采用二分法的解题思路，二分法主要是面向有序的数组且也满足二段性的数组，所谓二段性就是在一定的规则下能把该数组分成两个部分；

本题注意要点：

1、循环结束的条件：

左指针>右指针时，该循环结束；

2、关于中点的求解公式

一般采用左指针+整个数组一半的方法，而不是左右指针之差+1的和除以2，主要是防治后者会发生溢出；

综上所述，代码如下：

class Solution {public int search(int[] nums, int target) {int left = 0,right = nums.length-1;while(left <= right){//找到中间点，防止溢出int mid = left + (right-left)/2;if(nums[mid] < target){left = mid+1;}else if(nums[mid] > target){right = mid-1;}else{return mid;}}return -1;}
}

故此二分法的朴素解题模版如下所示：

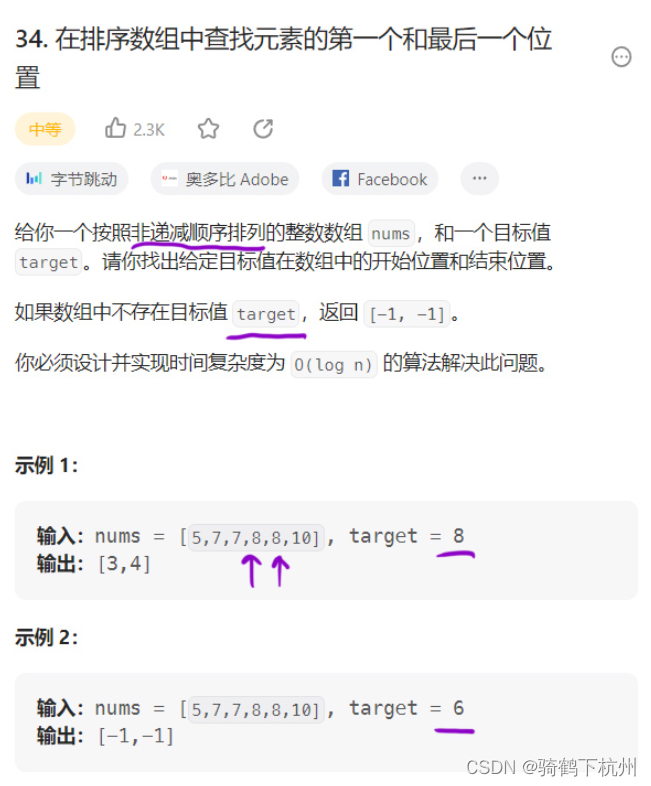
第二题

如上题所示，本题需要通过二分查找的方法来找到一个满足题意的连续数组，所以简单来说就需要查找原数组的左右端点；

上题中的原数组由于是非递减，锁说明满足二段性，即可以使用二分法；

步骤一：就是来分析如何查找左端点：

细节一：

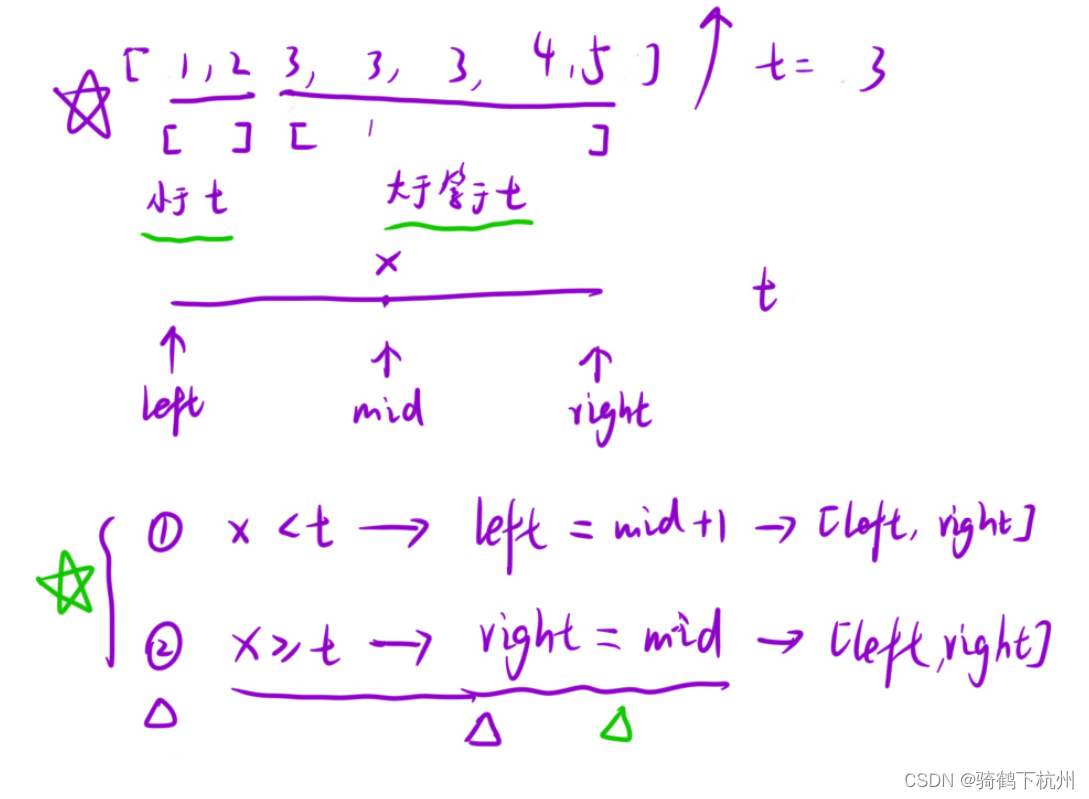
关于循环条件的分析，两种循环条件如下所示：

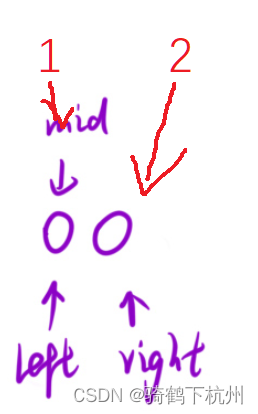
如上图分析，（1,2）左区域里面的数值永远小于t，（3,3,3,4,5）右区域里面的数可能大于等于t；

所以当mid指针所指的数值x接下来右如下分析：

x<t时，t值的位置在mid右边，所以更新左指针，left=mid+1，即得到一个新的循环区间；

x>=t时，t值的位置在mid的左边或者mid的位置，所以right=mid；

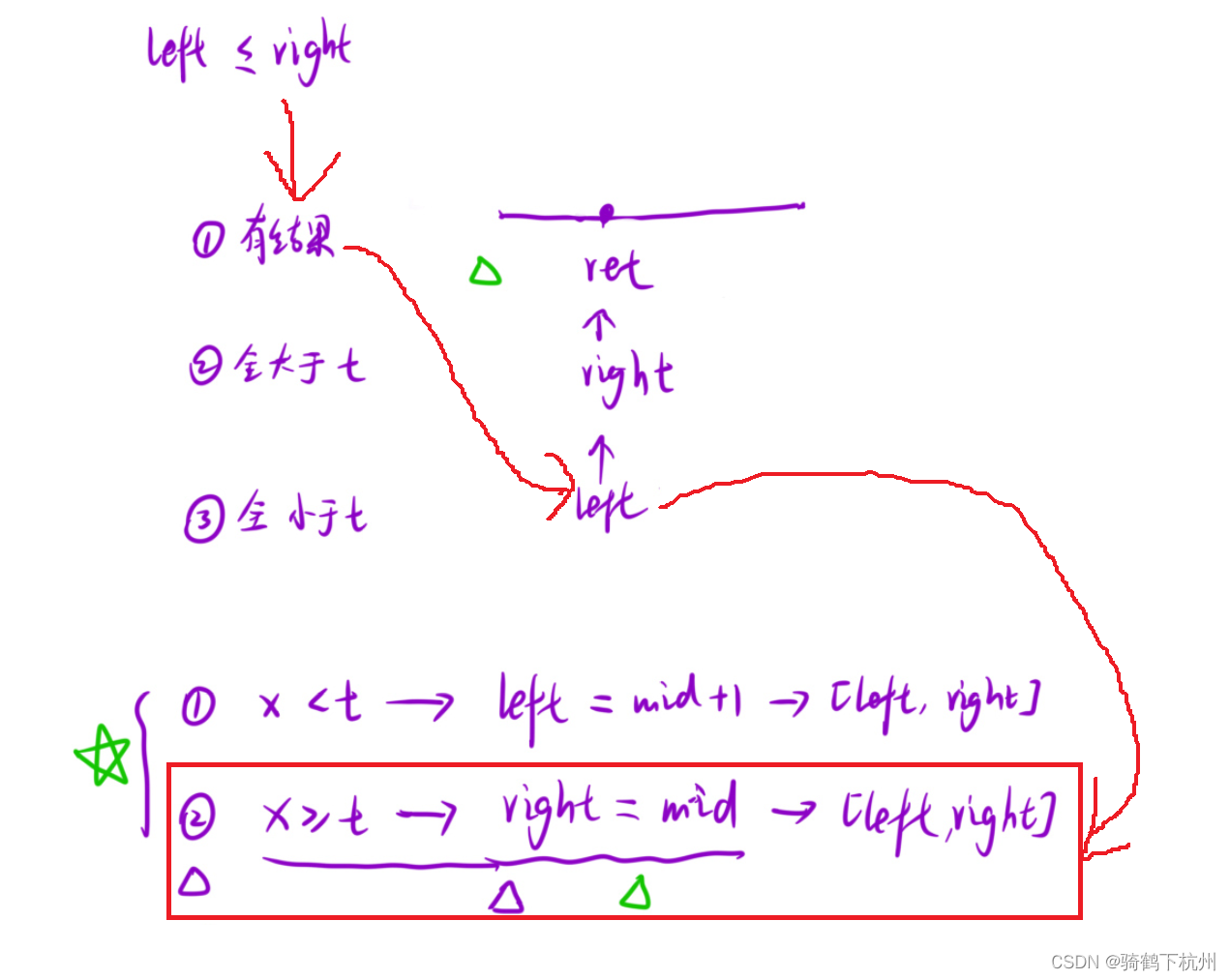
所以当我们的判断条件是left<=right时，做如下分析：

如果原数组里有我们需要的结果，左后左指针会与右指针重逢，且指向我们所求的端点，但是由于我们的判断条件，所以就会一直更新区间；分析图如下所示：

综上所述：

1、left=right的时候，就已经出现结果了，不需要在进行判断了；

2、如果在判断就会出现死循环；

细节二：

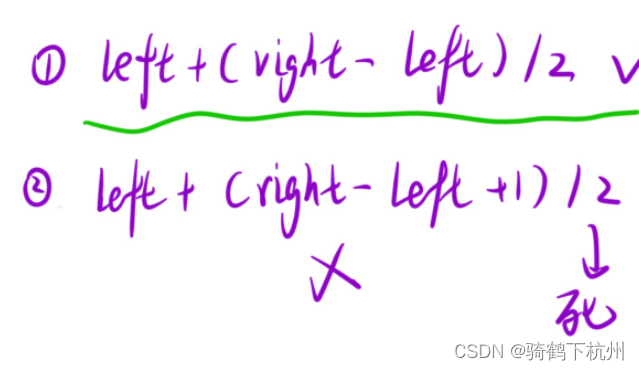
关于在循环条件时，我们进行中点计算的公式选择分析：

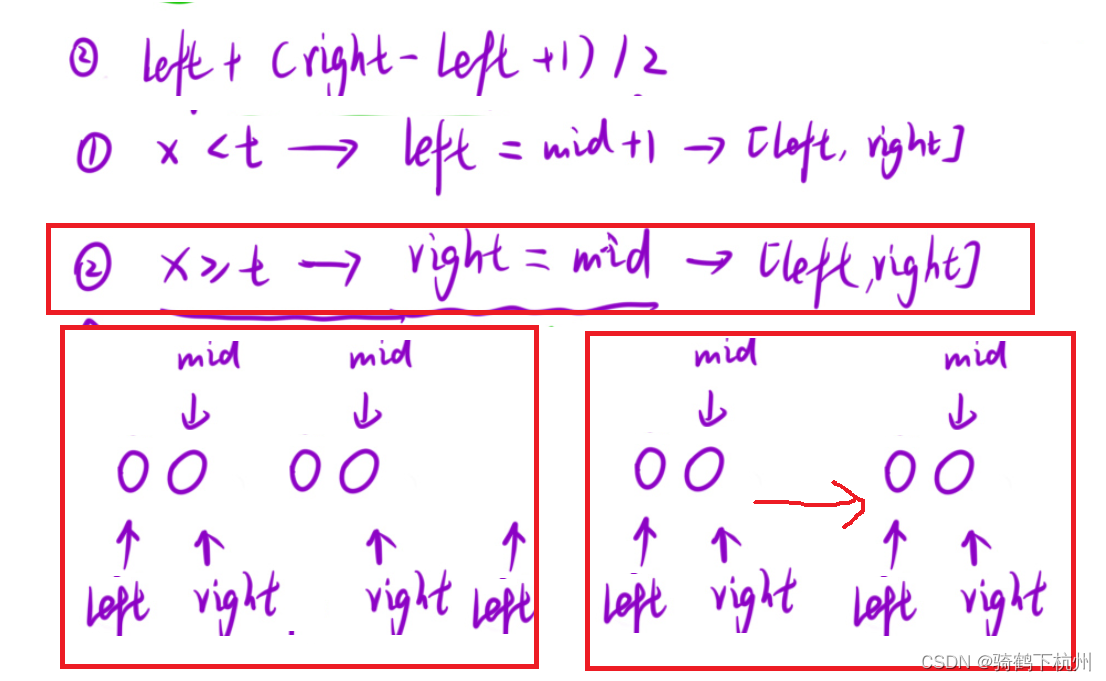
有下图所示，重点选择的公式有下面两种方式：

上面两种方法的区别就是当有长度为2的数组是，找到的中点事不同的；

第一种方法找到的中点是left，第二种方法找到的中点是right；

接下来讲第一种中点方法：



如上图所示，第一种中点选择时，

x<t时，左指针右移和右指针相等，则得到要判断的值；

         x>=t时，左指针右移两位，左指针在右指针的右边，则当前没有找到需要的点，循环结束；

        接下来讲第二种中点方法：

如上图所示，第二种中点选择时，

x<t时，左指针右移两位，左指针在右指针的右边，则当前没有找到需要的点，循环结束；

         x>=t时，右指针不变，则进入死循环；

步骤二：就是来分析如何查找右端端点：

细节一：

关于循环条件的分析，有上述左端点的分析，我们选择left<right；

细节二：

如上分析，我们选择

分析如下：

分析如上，代码如下：
class Solution {public int[] searchRange(int[] nums, int target) {int[] ret = new int[2];ret[0]= ret[1] = -1;if(nums.length == 0){return ret;}//1二分左端点int left = 0,right = nums.length-1;while(left < right){int mid = left +(right-left)/2;if(nums[mid] < target){left = mid+1;}else{right = mid;}}//此时做左右指针相遇，接下俩判断该相遇点的值是否为目标值if(nums[left] != target){return ret;}else{ret[0] = left;}//2、二分右端点left = 0;right = nums.length-1;while(left < right){int mid = left +(right-left+1)/2;if(nums[mid] <= target){left = mid;}else{right = mid-1;}}//此时做左右指针相遇，接下俩判断该相遇点的值是否为目标值if(nums[left] != target){return ret;}else{ret[1] = right;}return ret;}
}
解题经验如下：