1. BM24 二叉树的中序/后续遍历
要求:给定一个二叉树的根节点root,返回它的中序遍历结果。
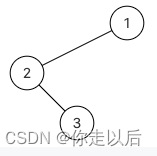
输入:{1,2,#,#,3}
返回值:[2,3,1]
1.1 自己的整体思路(与二叉树的前序遍历大致一样)
- 使用二叉树的前序遍历方法,递归完成二叉树元素的访问。
- 先遍历二叉树,求出二叉树的结点数量以后,再申请数组,这样节省内存大小。
- 二叉树的前中后序遍历,只需要改变访问根结点的代码位置,其与递归左子树和右子树的位置,代表是前中后序的一种。
#include <malloc.h>
#include <stdbool.h>
#include <stdint.h>
#include <stdio.h>
#include <string.h>
int TreeSize(struct TreeNode* root) { //判断二叉树有多少个结点if (root == NULL) {return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}
void visit_root(struct TreeNode* root, int* arr,int *a){ //访问根结点*(arr + *a) = root->val; //存下根结点元素(*a)++; //索引++
}void Preorder(struct TreeNode* root, int* arr,int *a){ //遍历二叉树if (root!=NULL) {Preorder(root->left,arr,a); //递归左结点visit_root(root,arr,a); //访问根结点 //如果把这一行放到下面一行,就是后序遍历,其他的代码不用变的Preorder(root->right,arr,a); //递归右结点}}
int* inorderTraversal(struct TreeNode* root, int* returnSize ) { //中序遍历// int n; //这里没有初始化,导致程序卡死了int n = 0;int *i = &n;int count = TreeSize(root); //计算二叉树有多少结点printf("val = %d\r\n",count);int *array = (int *)malloc(count * sizeof(int)); //申请一个空数组Preorder(root, array, i); //遍历二叉树*returnSize = *i;return array;
}
1.2 小结
1.2.1 求二叉树结点的个数
int TreeSize(struct TreeNode* root) { //判断二叉树有多少个结点if (root == NULL) {return 0;}return TreeSize(root->left) + TreeSize(root->right) + 1;
}
假设这个二叉树如下所示:
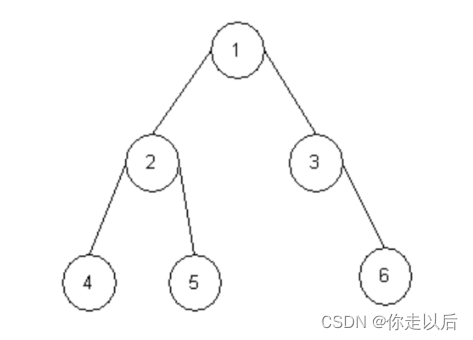
第一次进到这个程序中:结点1不为NULL,返回的是TreeSize(结点2) + TreeSize(结点3) + 1;
运行TreeSize(结点2) :结点2不为NULL,返回的是TreeSize(结点4) + TreeSize(结点5) + 1;
运行TreeSize(结点4) :结点4不为NULL,返回的是TreeSize(NULL) + TreeSize(NULL) + 1,也就是返回的0 + 0 +1 =1;
返回上面一层TreeSize(结点5):结点5不为NULL,返回的是TreeSize(NULL) + TreeSize(NULL) + 1,也就是返回的0 + 0 +1 =1;目前TreeSize(结点2) 返回的值就是1+1+1 = 3;
运行TreeSize(结点3):结点3不为NULL,返回的是TreeSize(NULL) + TreeSize(结点6) + 1;
运行TreeSize(结点6):结点6不为NULL,返回的是TreeSize(NULL) + TreeSize(NULL) + 1,也就是返回的0 + 0 +1 =1;目前TreeSize(结点3) 返回的值就是0+1+1 = 2;
所以整体TreeSize(结点2) + TreeSize(结点3) + 1 = 3 + 2 + 1 = 6,也就计算出来了二叉树结点的个数。
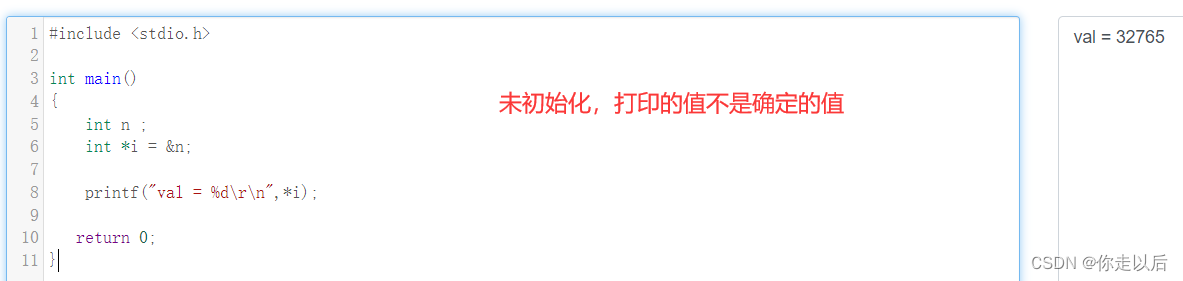
1.2.2 使用指针时,未初始化变量初值
使用指针时,未初始化变量初值,导致程序报错。
int n;
int *i = &n;
2. BM28 二叉树的最大深度
要求:求给定二叉树的最大深度,深度是指树的根节点到任一叶子节点路径上节点的数量。最大深度是所有叶子节点的深度的最大值.
这个题,没有什么思路,看视频讲解的方法,代码如下:
#include <stdio.h>
int maxDepth(struct TreeNode* root ){int n1 = 0;int n2 = 0;if (root == NULL) {return 0;}n1 = maxDepth(root->left);n2 = maxDepth(root->right);return n1 > n2 ? n1 + 1 : n2 + 1;
}
假设这个二叉树如下所示,还是以下面这个二叉树为例,看这个代码具体运行的步骤:
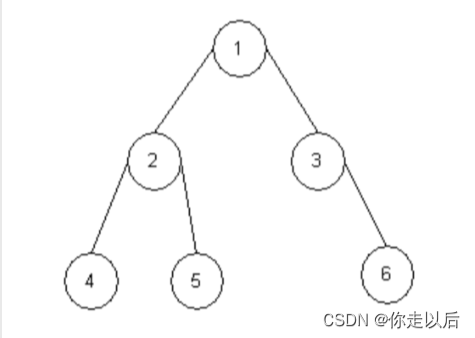
第一次进到这个程序中:结点1(根结点)不为NULL,运行 n1 = maxDepth(根结点的左结点(结点2));
因为结点2不为NULL,此时传入结点2进入函数:运行n1 = maxDepth(结点2的左结点(结点4));
因为结点4不为NULL,此时传入结点4进入函数:运行n1 = maxDepth(结点4的左结点(NULL)),并返回了n1 =0。
因为结点4的左结点为NULL,程序会执行下面一句,n2 = maxDepth(结点4的右结点(NULL)),并返回了n2 =0。
所以对于结点4,n1 = n2=0,程序会返回1。这里也就是结点2的左结点,n1 = maxDepth(结点2的左结点(结点4)),这里的n1 = 1;
此时程序会返回到,结点2上面,运行n2 = maxDepth(结点2的右结点(结点5));
因为结点5不为NULL,此时传入结点5进入函数:运行n1 = maxDepth(结点5的左结点(NULL)),并返回了n1 =0。
因为结点5的左结点为NULL,程序会执行下面一句,n2 = maxDepth(结点5的右结点(NULL)),并返回了n2 =0。
所以对于结点5,n1 = n2=0,程序会返回1。这里也就是结点2的右结点,n2= maxDepth(结点2的右结点(结点5)),这里的n2 = 1;
此时对于结点2来说,n1=1,n2=1,所以会返回2。这里也就是结点1的左结点,n1 = maxDepth(结点1的左结点(结点2)),这里的n1 = 2;
此时程序会返回到,结点1上面,运行n2 = maxDepth(结点1的右结点(结点3));
因为结点3不为NULL,此时传入结点3进入函数:运行n1 = maxDepth(结点3的左结点(NULL)),并返回了n1 =0。
因为结点3的左结点为NULL,程序会执行下面一句,n2 = maxDepth(结点3的右结点(结点6))。
因为结点6不为NULL,此时传入结点6进入函数:运行n1 = maxDepth(结点6的左结点(NULL)),并返回了n1 =0。
因为结点6的左结点为NULL,程序会执行下面一句,n2 = maxDepth(结点6的右结点(NULL)),并返回了n2 =0。
所以对于结点6,n1 = n2 = 0,程序会返回1。这里也就是结点3的右结点,n2 = maxDepth(结点3的右结点(结点6)),这里的 n2 = 1;
此时对于结点3来说,n1 = 0,n2 = 1,所以会返回2。也就是结点1中的n2 = maxDepth(结点1的右结点(结点3)) = 2;
此时对于结点1来说,n1 = 2,n2 = 2,所以会返回3。程序结束,二叉树的最大深度是3。
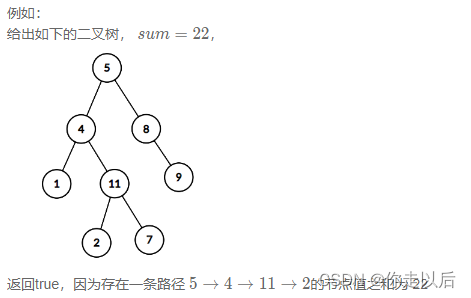
3. BM29 二叉树中和为某一值的路径
要求:给定一个二叉树root和一个值 sum ,判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。
1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点
2.叶子节点是指没有子节点的节点
3.路径只能从父节点到子节点,不能从子节点到父节点
4.总节点数目为n
这个题,也没有什么思路,看视频讲解的方法,代码如下:
bool bianli(struct TreeNode* root, int sum, int sum1){ //遍历一个子树,必须要返回一个值if (root == NULL) {return false;}sum1 += root->val; //求和if (root->left == NULL && root->right == NULL) {if (sum1 == sum){return true;}else{return false;}}bool leftHasPath = bianli(root->left, sum, sum1);bool rightHasPath = bianli(root->right, sum, sum1);return leftHasPath || rightHasPath;
}bool hasPathSum(struct TreeNode* root, int sum){//如何遍历一个子树// int * arr = (int *)malloc(1000*sizeof(int)); int a = 0; //求和return bianli(root,sum,a);
}
假设这个二叉树如下所示,还是以下面这个二叉树为例,看这个代码具体运行的步骤:(结点每一排依次称为结点1,2,3…)
第一次进到这个程序中:结点1(根结点)不为NULL,sum1 = 5; 然后进入这一句:bool leftHasPath = bianli(结点2, 22, 5);
sum1 = 5 + 4 = 9; bool leftHasPath = bianli(结点4, 22, 9); 这是结点3的左结点。
sum1 = 9 + 1 = 10;return false; 返回上一层循环,返回到结点3, bool rightHasPath = bianli(结点5, 22, 9);因为到结点3的时候,sum1的值就是9。
sum1 = 9 + 11 = 20; bool leftHasPath = bianli(结点7, 22, 20);
sum1 = 20 + 2 = 22; return true;综上就是leftHasPath = false; rightHasPath = true;程序会继续运行,直到遍历完所有可能的路径。最终会返回true。
改进代码如下,找到一条路径后就会停止(不会遍历所有的路径的):
bool findPath(struct TreeNode* node, int targetSum, int currentSum) {if (node == NULL) {return false;}currentSum += node->val;if (node->left == NULL && node->right == NULL && currentSum == targetSum) {return true;}bool foundInLeft = findPath(node->left, targetSum, currentSum);if (foundInLeft) {return true; // 找到路径,立即中断递归}bool foundInRight = findPath(node->right, targetSum, currentSum);if (foundInRight) {return true; // 找到路径,立即中断递归}return false; // 未找到路径
}bool hasPathSum(struct TreeNode* root, int sum){//如何遍历一个子树// int * arr = (int *)malloc(1000*sizeof(int)); int a = 0; //求和return findPath(root,sum,a);
}
假设这个二叉树如下所示,还是以下面这个二叉树为例,看这个代码具体运行的步骤:
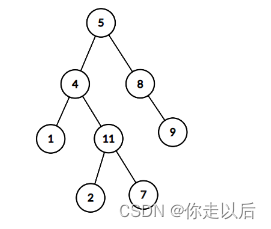
第一次进到这个程序中:结点1(根结点)不为NULL,currentSum = 5; 然后进入这一句:bool foundInLeft = findPath(结点2, 22, 5);
currentSum = 5 + 4 = 9; bool foundInLeft = findPath(结点4, 22, 9);
currentSum = 9 + 1 = 10; bool foundInLeft = findPath(NULL, 22, 10); return false;并返回到了结点2了。
bool foundInRight = findPath(结点5, 22, 9); currentSum = 9 + 11 = 20; bool foundInLeft = findPath(结点7, 22, 20);
currentSum = 20 + 2 = 22; return true; 程序不会会继续运行,不会遍历完所有可能的路径。当找到路径后,递归会立即中断,从而停止遍历。