原理解释
电路实现
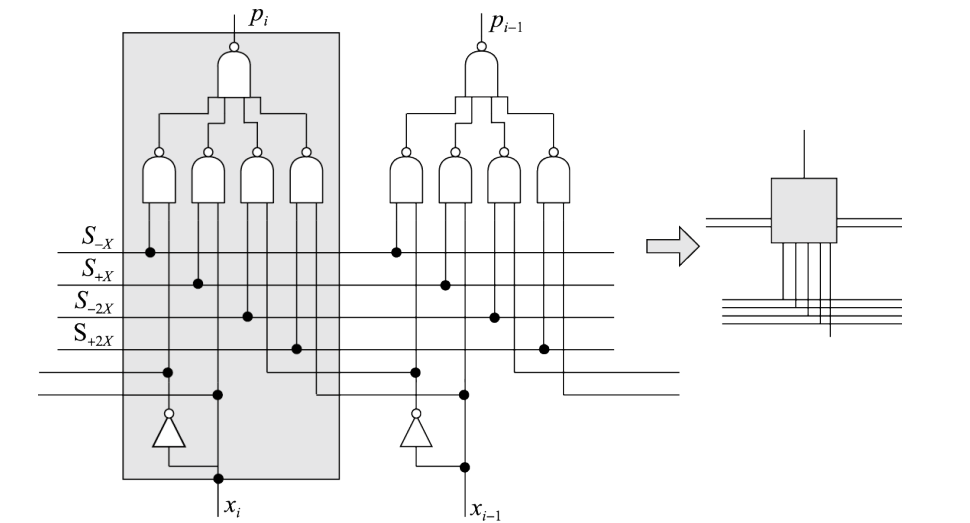
以Radix-4 Booth编码为例,Booth乘法的核心是部分积的生成,需要生成\(N/2\)个部分积,每个部分积与\([X]_补\)有关,存在\(-X,-2X,+X,+2X,0\) 这五种可能,其中减去\(X_{补}\)的操作可以认为是按位取反的\(X_{补}\)在末尾+1。为了硬件实现方便,可以将末位1操作提取出来,假设\(X_{补}\)的二进制格式为\(x_6x_5x_4x_3x_2x_1x_0\),假设部分积\(P=p_7p_6p_5p_4p_3p_2p_1p_0+c\),那么有:

当部分积微2X时,可以认为X输入左移一位,此时\(p_i=x_{i-1}\)相等。如果部分积的选择为\(-X/-2X\),则此处对\(x_i\)或\(x_{i-1}\)取反,并设置最后的末位进位\(c=1\)。
由此可以得到每一位\(p_i\)的逻辑表达式为:
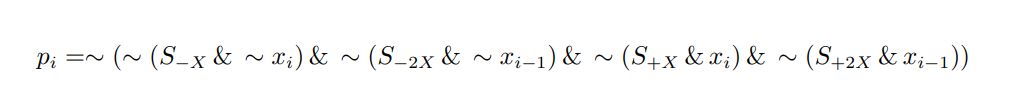
Booth结果选择逻辑如下所示:
部分积生成过程中需要利用\(y_{i-1},y_i\)和\(y_{i+1}\)这三个信号来生成需要用到的\(S_{-X},S_{-2X},S_{X},S_{2x}\)的选择信号,通过卡诺图化简可以得到:
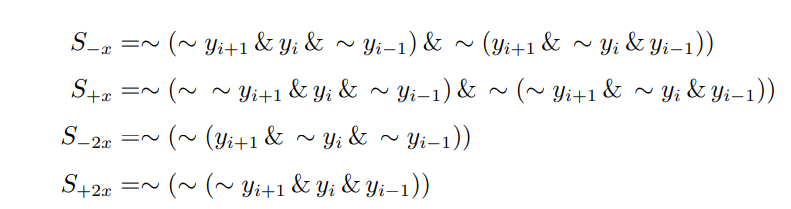
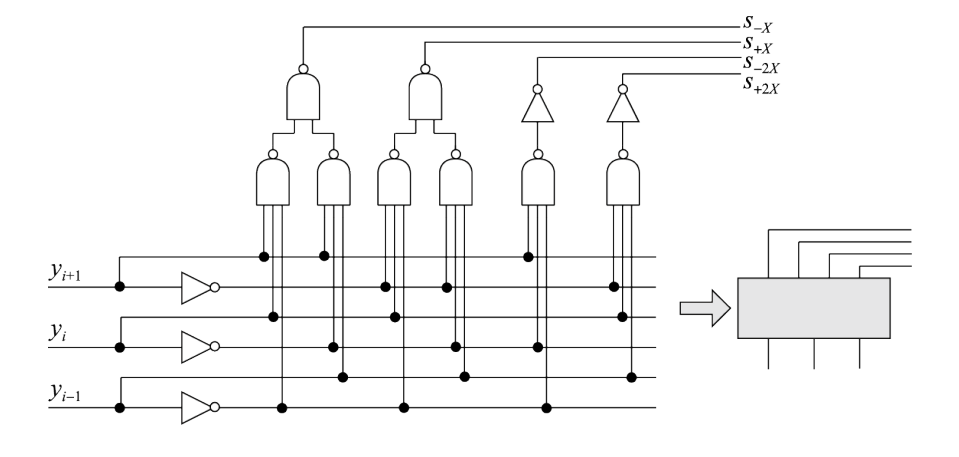
选择信号生成部分的逻辑图如下所示:
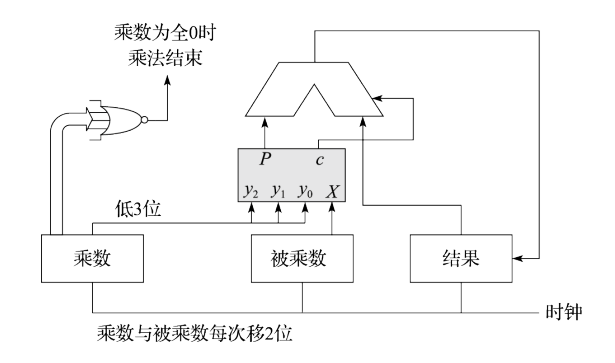
通过组合上述两个部分,可以形成每个Booth部分积的逻辑图,调用该逻辑通过移位加法策略可以实现两位Booth补码乘的结构。
乘法操作开始时,乘数右侧需要补1位的0,结果需要预置为全0.在每个时钟周期的计算结束后,乘数算术右移两位,被乘数左移两位,直到乘数全为0,乘法结束。
对于N位补码乘法,操作可以在N/2个时钟周期完成。被乘数、结果、加法器和Booth核心的宽度都为2N位。
代码实现
/*
* 基4的booth编码的单周期有符号乘法器
*/module booth_multiplier_base4 #(parameter DATA_WIDTH = 8 // 数据位宽应该为2的指数
)( input [DATA_WIDTH-1 : 0] a, input [DATA_WIDTH-1 : 0] b, output reg [2*DATA_WIDTH-1 : 0] product,input clk
); integer i; reg [2:0] booth_bits [DATA_WIDTH/2-1:0]; reg [DATA_WIDTH:0] b_extended;reg [2*DATA_WIDTH:0] partial_product [DATA_WIDTH/2-1:0]; reg [2*DATA_WIDTH-1:0] a_pos, a_neg, a_extend; always @(posedge clk) begin b_extended = {b, 1'b0}; // 这里我补了个0,防止索引超出界限a_extend = {{DATA_WIDTH{a[DATA_WIDTH-1]}}, a}; // 符号位扩展 ,之前忘记扩展找了好久a_pos = a_extend;a_neg = ~a_extend + 1'b1; // 补码运算product = 0;for (i = 0; i < DATA_WIDTH/2; i = i + 1) begin booth_bits[i] = {b_extended[2*i+2], b_extended[2*i+1], b_extended[2*i]}; case (booth_bits[i])/*$\sum_{i=0}^{\frac{n}{2}-1} (-2 \cdot b_{2i+2} + b_{2i+1} + b_{2i})$ // LaTex{ b(2i+2), b(2i+1), b(2i) } :=000: 0;001: 1;010: 1;011: 2;100: -2;101: -1;110: -1;111: 0;*/ 3'b000, 3'b111: partial_product[i] = 9'd0; 3'b001, 3'b010: partial_product[i] = a_pos;3'b011: partial_product[i] = a_pos << 1;3'b100: partial_product[i] = a_neg << 1;3'b101, 3'b110: partial_product[i] = a_neg; endcase endfor (i = 0; i < (DATA_WIDTH/2-1); i = i + 1) beginproduct = product + (partial_product[i] << (2*i)); // Shift and accumulateendend endmodule